HMT-final 2015

Finalresultat

För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla uppgifter!

På delad andraplats kom två Lundabor också, nämligen Anna-Lisa Rathsman och Hugo Eberhard. Hela resultatlistan kan du se på HMT:s hemsida.


Björn och Valentina
Jag och vinnaren av HMT 2015

Finalproblemen

Prova att lösa uppgifterna själv!

1. Lotta väljer slumpmässigt två olika tal bland talen 1, 2, 3, 4, 5, 6, 7, 8 och 9. Hon beräknar därefter deras produkt. Hur stor är sannolikheten att produkten är ett ensiffrigt tal?

2. Parken Parc des Mathématiques är formad som ett kvadratiskt rutnät med 5×5 trädgårdar. Två trädgårdar anses vara grannar om de har en gemensam sida (men inte om de bara har ett gemensamt hörn). Om man placerar en vakt i en trädgård så kan den vakta den parterren samt alla grannar.

a) Placera ut sju vakter i parken så att alla 25 trädgårdarna är vaktade.

b) Visa att det inte går att vakta hela parken med fem vakter.

3. I kvadraten ABCD dras fyra linjer: från hörnet A dras en linje till mitten av sidan CD, från B till mitten av sidan AD, från C till mitten av sidan AB och från D till mitten av sidan BC. Hur stor är fyrhörningen som bildas i mitten i förhållande till hela kvadraten?

4. I 3×3-rutnätet är vissa radprodukter och kolumnprodukter utsatta. Finn alla möjliga sätt att placera samtliga siffror från 0 till 8 i rutnätet så att produkterna blir korrekta.

1415f4

5. En oändlig talföljd a1, a2, a3,… har egenskapen att för alla positiva heltal m och n gäller

a_m + a_n = a_{mn} + a_{m+n}

Vidare vet vi att a3 = 2015. Bestäm a2015.

6. Aladdin önskar sig tre böcker med sagor. Varje bok skall ha två tusen och fjorton sagor. Var och en av sagorna kan vara antingen spännande eller romantisk. Dock kommer hans käresta att ta en av böckerna eftersom hon också vill läsa sagor.

Aladdin förklarar för anden att han kommer läsa två sagor varje natt, en från varje bok som han har kvar. Självklart läser han dem i den ordning de står i böckerna. ”Men”, förklarar Aladdin, ”jag vill ha omväxling, så ibland vill jag ha två olika typer av sagor och ibland två lika typer, och jag kräver att vid precis hälften av nätterna få en romantisk och en spännande saga”.

Kan anden ge Aladdin tre böcker så att alla Aladdins önskemål är uppfyllda, oavsett vilken bok hans käresta tar bort?

Statistik

Tävlingen innehöll flera svåra problem. Som mest kan man få 7 poäng på ett problem, men man kan också få delpoäng. Snittresultaten blev sådana:
* Problem 1: 5.18
* Problem 2: 5.98
* Problem 3: 2.76
* Problem 4: 3.70
* Problem 5: 2.64
* Problem 6: 1.08

Så det var problem 2 som var lättast och inte problem 1 som vi i juryn trodde.

På graden kan du också se hur många finalister (y-axeln) som fick ett visst antal poäng på respektive problem.
statistik_hmtfinal2015

Arbetet i jurygruppen

I år var jag en av medlemmarna i jurygruppen och hjälpte till att ta fram problemen. Jag tror att juryn kan vara stolta över resultatet, då vi fick en tävling med roliga varierande problem. De flesta av dem innehöll någon twist och det var inte självklart hur man skulle lösa dem. Ändå är de möjliga att lösa eller vad tycker du? Är det något speciellt problem som du tycker är extra snyggt?

Själv gillar jag problem nummer 6 väldigt mycket. Från början hade den en annan formulering:

”Aladdin önskar sig ett rutnät med 2014 rader och 3 kolumner, där varje ruta är färgad antingen turkos eller gredelin. Han önskar sig specifikt ett rutnät som är sådant att vilka två kolumner han än väljer så är antalet rader där rutorna i de två kolumnerna har samma färg lika stort som antalet rader där rutorna har olika färg. Går det att uppfylla Aladdins alla önskningar?”

Vi valde att formulera om det till en mer konkret situation med sagoböcker. Olika människor föredrar olika formuleringar, men i slutändan ska det ju inte spela någon roll. Välj vilken formulering du vill och försök lösa Aladdin-problemet!

Fjärde träffen med Matteklubben, åk 7-9

Du kan läsa om vad som har hänt på de tidigare träffarna här: första träffen, andra träffen och tredje träffen.

Introduktion till informationsteori

Vi började lektionen med leken ”Gissa talet”. Jag tänkte på ett tal mellan 1 och 10 och eleverna fick ställa ”Ja/Nej”-frågor för att försöka bestämma vilket tal jag tänkte på. Jag tror att det tog 5 frågor för dem att bestämma talet.

Här ska man vara tydlig om vad som gäller sista frågan. Ska man veta vilket tal det är efter x frågor eller ska man med fråga nummer x bekräfta talet? I uppgifterna räcker det att man vet vilket tal det ska vara, men man behöver inte fråga specifikt om det. Till exempel, om man vet att talet är 3 eller 4, frågar ”Är talet 3?” och får svaret ”Nej”, så behöver man inte fråga något mer, utan talet räknas som gissat.

Jag undrade sedan om hur många frågor som krävdes som mest för att garanterat gissa ett tal mellan 1 och 10 på det här sättet. Eleverna tänkte att 5 frågor räckte, men var osäkra på om 4 frågor var nog.

Startuppgiften var till för att presentera idén informationsteori, det vill säga hur mycket information man egentligen får när man det bara finns ”Ja” och ”Nej” som svar på frågorna. Hur mycket information är nog för att gissa talet?

Informationsteori: problemlösning och genomgång

Vi delade ut dagens uppgifter sedan och eleverna löste dem, mestadels på egen hand. För att alla ändå skulle ta del av varandras idéer körde vi genomgångar på tavlan allt eftersom. Då kunde eleverna snappa upp lösningssätt direkt för att eventuellt tillämpa dem på senare problem.

Problemen försökte jag ordna i svårighetsgrad, så att man successivt skulle sättas in ämnet och idéerna. Efter varje problem skriver jag dialoger jag hade med enskilda elever, samt med gruppen när vi gick igenom respektive uppgift på tavlan.

1. Du och en kompis spelar ett spel där ni ska ge varandra hemliga signaler. Ni har kommit överens om att man antingen kan blunda med ena ögat, med båda ögonen eller ha ögonen öppna, samt röra på vänster lillfinger eller hålla vänstra lillfingret still (alla andra rörelser spelar ingen roll, och görs för att avleda motståndarna från systemet). Hur många olika kombinationer av signaler kan du göra?

Elev: Jag vet inte om det räknas som samma eller olika om man blundar med höger- eller vänsterögat.
Lärare: Vi räknar det som olika i den här uppgiften.
Elever: Då har jag ritat upp alla möjligheter och det blir 4*2 = 8.
Lärare: Rätt!

2. Vilgot tänker på ett heltal mellan 1 och 8. Theo ställer frågor, som Vilgot bara kan svara ”ja” eller ”nej” på. Theo vill bestämma talet.
a) Kan han bestämma talet på tre frågor?
b) På två frågor?


Elev: Så här kan man göra med tre frågor (visar frågorna som man kan ställa och hur man fortsätter beroende på svar).
Lärare: Javisst, tror du det går med två frågor?
Elev: Nej, inte alltid.
Lärare: Varför inte?
Elev: Vet inte riktigt..

Gruppdisskussion:
Lärare: Ni har kommit på olika sätt att ställa frågor så att man kan gissa talet garanterat på tre försök. Går det att hitta på frågor som alltid är desamma oavsett vad personen svarar?
Elever: De första två går. Först frågar man om talet är större än 4 och sedan huruvida det är udda eller jämnt.
Lärare: Japp, det funkar att ställa den andra frågan oavsett svaret på den första. Men går det med alla tre? Tänk på det…
En annan lärare: Jag vet hur man gör, men det är ganska komplicerade frågor…

Lärare: Det går inte med två frågor, varför inte?
Elev: (Berättar om halvering)
Lärare: Precis, det är en möjlig förklaring, här är en annan! (Berättar om hur man beräknar information för att särskilja mellan möjliga kandidater.)

3. På en balansvåg kan man jämföra vikten i vänsterskålen med vikten i högerskålen. Vågen kan antingen visa balans eller att vänsterskålen är tyngre eller att högerskålen är tyngre. Emilia experimenterar med att väga olika mynt för att jämföra dem med varandra. Klara antecknar resultatet av varje vägning på ett papper.

Emilia gör 5 vägningar. På hur många sätt kan Klaras protokoll se ut?

Elev: Första vägningen kunde se ut på tre sätt. Sedan är det liksom en förgrening, där det kan se ut på tre sätt till efteråt. Jag försöker skriva upp alla kombinationer.
Lärare: På hur många sätt kunde då protokollet se ut efter 2 vägningar?
Elev: 3*3 = 9
Lärare: Och efter tre? Och efter fem?
Elev: Ahaa.. 35.

4. 9 mynt ser likadana ut. Man vet att exakt ett av dem är falskt (men man vet inte vilket). Man vet även att alla äkta mynt väger lika mycket samt att det falska myntet är något lättare. Hur kan man bestämma det falska myntet med högst två vägningar? Går det att göra det på en vägning?

Elev: (Visar hur man gör med två vägningar).
Lärare: Rätt. Varför går det inte att göra på en vägning?
Elev: Hur man än gör så blir det en hög över som man inte vet något om.
Lärare: Men kan man inte lämna 1 mynt över och väga de andra?
Elev: Jo, men då vet man fortfarande inte vilket som är falskt, om det inte blir lika.

Det var inte så många som kopplade ihop uppgift nummer 3 och nummer 4. Jag förklarade sedan högt att man kan göra precis som i uppgift 2, fast istället för ”halvering” har vi ”tredelning”. Eller, om man gör på det andra sättet, så ska vi ha resultat som skiljer på 9 mynt, men vi kan bara få 3 olika resultat (”protokoll”).

5. Det finns 6 mynt, varav 2 är falska och väger mindre än de riktiga. Hur många vägningar behöver du som minst för att säkerligen bestämma de båda falska mynten?

En av eleverna visade korrekt resonemang för tre vägningar, men det var en annan lärare som kontrollerade detta. Tillsammans gick vi igenom den lösningen på tavlan. Sedan gällde det att motivera varför detta inte gick att göra på två vägningar.

Lärare: Nu är det inte ett mynt man ska bestämma, utan två. Hur många ”situationer” behöver vi skilja emellan? På hur många sätt kan 2 mynt av 6 vara falska?
Elever: (Kommer fram till att det är 15).
Lärare: Så vi har 15 misstänkta situationer. På hur många sätt kan protokollet se ut efter 2 vägningar?
Elever: 9.
Lärare: Alltså går det inte att skilja mellan 15 olika situationer, så det går inte att säkerligen bestämma de falska mynten på 2 vägningar.

6. En liksidig triangel är uppdelad i 9 små kongruenta liksidiga trianglar. Benni markerade en av de små trianglarna med osynligt bläck. Ivar kan peka på en triangel, vars sidor går längs med de utritade linjerna och då måste Benni svara huruvida den markerade triangeln ligger i den Ivar pekar ut.

Hur många frågor behöver Ivar som minst för att garanterat hitta den markerade triangeln?

Denna uppgift hanns inte med, utan den blev kvar i läxa. Jag förtydligade vilka regler som gällde på tavlan, nämligen visade upp exempel på trianglar med olika storlekar som man kunde peka ut vid frågor.

Ladda ner uppgifterna för utskrift

 

Skottväxling

Andra (lite mindre) halvan av lektionen körde vi mattetävlingen ”Skottväxling”. Eleverna delades upp i lag om tre personer. Lagen fick de kreativa namnen A, B, C och D.

Reglerna till Matematisk Skottväxling är följande:

Varje uppgift ger ditt lag rätt till ett skott. Ange ert svar på en papperslapp och skriv vilket lag ni skjuter på. Var femte minut verkställs anmälningar i samma ordning som de har kommit. Fel svar räknas som ett ett klickskott och minskar er träffsäkerhet. Vid rätt svar slumpas det (beroende på er träffsäkerhet) huruvida ni träffar eller missar.}

Träffar ni så minskas den träffade lagets styrka med 1/5 av er styrka (en kvot avrundas neråt).
Är er styrka mindre än 15, så minskar er motståndares styrka med 3.
Efter spelets slut vinner den som är starkast då. Ursprungliga styrkor är 100.

Den ursprungliga träffsäkerheten är 2:2, det vill säga 2 chanser att träffa och 2 att missa.
Rätt svar ökar era chanser att träffa med 1, fel svar ökar era chanser att missa med 1.
Uppgifterna är indelade i 2 delar, del 1 ges ut i början, del 2 ges ut 20 minuter efter start. Spelet är slut antingen när det har gått 40 minuter eller när alla har skjutit sina 10 skott.
Ett lag får lämna svar på varje uppgift i godtycklig ordning och vid valfri tidpunkt, men inte mer än en gång per uppgift.

(Detta stod inte i reglerna, men vi förtydligade vid start att chanserna förändrades innan skotten avfyrades).

Vi körde tävlingen i två delar med 5 problem i varje. De flesta inlämnade svar var korrekta, så många skott under tävlingen träffade. Vi skrev upp protokoll direkt under tävlingens gång över vem som sköt på vem och hur mycket lagen minskade i styrka. Det var roligt att följa hur vissa lag ”förklarade krig” mot varandra då och då. Det var ganska mycket action och vi fyra lärare var sysselsatta nästan hela tiden!

Detta är ju en lek som det är svårt att ha vinnande strategi i, eftersom man alltid kan skjuta på den som leder. Men man kan vara lite taktisk med tidpunkter då man lämnar in sina svar.

I slutändan stod lag D som segrare efter en ganska jämn match! Tyvärr har jag inte sparat poängtabellen.

Här kan du själv prova att lösa Skottväxling-uppgifterna. Fråga mig om du vill veta de rätta svaren. Notera att den sista uppgiften på del B är lite annorlunda från de andra. Den är baserad på en uppgift som en av eleverna på Matteklubben kom på. Den var dock ändrad för att eleven inte skulle ha för mycket fördel i tävlingen.

På del A var uppgift 2 och 3 lättast och på uppgift 5 gavs flest felaktiga svar. Vi gick igenom den uppgiften i slutet av lektionen.

Ladda ner del A för utskrift

På del B gavs flest rätt svar på uppgift 3 och 4, medan 2 och 1 svarade de flesta fel på. Ingen löste uppgift nummer 5 (den var nog överkurs).

Ladda ner del B för utskrift

Prova gärna att organisera skottväxling i den egen klass! Det är roligt för de flesta, eftersom vilket lag som helst, oavsett styrka, har möjlighet att vinna. Anpassa uppgifterna efter elevernas nivå.

Hos oss var tävlingen i alla fall populär, vilket märktes på utvärderingarna. De flesta av eleverna i den här gruppen känner inte varandra så det var bra att ”tvinga” dem att samarbeta lite.

Utvärdering

I slutet av lektionen fick eleverna svara på följande frågor om matteklubben:

Vilken matteklubben-träff tyckte du bäst om?

Vilket tema var mest intressant?

Vilket avsnitt var svårast?

Vad kan fungera bättre med matteklubben?

Vill du se någon förändring inför nästa termin? Vad i så fall?

Vill du fortsätta gå på Matteklubben nästa termin (ringa in)?

Ja Nej Kanske

Det är lite konstigt ser jag nu att vi inte bad eleverna att bedöma deras insats, så som vi gjorde i de yngre årskursna. Vi missade nog helt enkelt att inkludera den frågan.

Resultatet av utvärderingarna

Efter varje svar står siffran för antalet elever som gav det svaret.

Vilken matteklubben-träff tyckte du bäst om?

– Den sista 7 (2 säger: för att det var tävling)

– Vet inte 2

– Nr 3

– Ingen var utmärkande

– Informationsteori

Vilket tema var mest intressant?

– Alla var ungefär lika intressanta 2

– Vinklar

– Informationsteori 5

– Delbarhetsprinciper

– Vet inte/ej svar 3

Vilket avsnitt var svårast?

– Vinklar 4

– Vet inte/ej svar 5

– Alla var bra anpassade så ingen var speciellt svår

– Andra lektionen 3

Vad kan fungera bättre med matteklubben?

– Ingen aning/Vet ej/ej svar 9

– Lättare uppgifter

– Mer tävlingar

– Tydligare vilken sal man är i

– Lite tidigare möten

Vill du se någon förändring inför nästa termin? Vad i så fall?

– Att varje person ska få göra en uppgift och så kan vi lösa varandras

– Vet ej/ej svar 7

– Lite tidigare möten

– Mer tävlingar

– Lättare uppgifter

– Jag vill ha det tidigare i veckan

– Enda förändringen jag vill se är hos mig själv och mina kunskaper. Matteklubben är bra!

Vill du fortsätta gå på Matteklubben nästa termin (ringa in)?

Ja 6
Nej 0
Kanske 6

Tankar inför nästa termin

Jag tänker precis som eleverna: mer tävlingar, bättre anpassad svårighetsgrad! Jag ska försöka köra tävlingar var tredje gång även i den här gruppen eller kanske en större tävling var fjärde gång och en minitävling var fjärde gång. Vi behöver även att träna på fler redovisningsformer, t.ex. ha skriftliga lösningar någon gång. Tyvärr kan inte vi ha Matteklubben tidigare på dagen, på grund av svårigheten att boka salarna tidigare.

Med en så pass liten grupp borde jag ha hunnit lära mig allas nivå och styrkor, men det har visat sig vara rätt svårt. Eleverna har varit ganska tysta under lektionerna och jag har själv uppmanat dem till att redovisa lösningar, åtminstone till mig. Vi får se om det blir bättre med tiden, att eleverna känner sig säkra på sin problemlösningsförmågor samt att det är helt ok att ha fel på Matteklubben. Nästa termin kan bara bli bättre! :)

Fjärde träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan läsa om första, andra och tredje träffen med gruppen.

Nytt sätt att sitta

Den sista gången för terminen testade vi en ny bordsuppställning. Vanligtvis brukar vi behålla lektionssalen som den är, det vill säga ha 4 långa rader med bord och stolar, uppdelade i tre sektioner (den mittersta sektionen är störst). Det finns egentligen plats för cirka 40 personer, men vår grupp är inte lika stor längre (det brukar nu komma mellan 20 och 30 barn). Dels för att skapa naturlig ”gruppkänsla” och dels för att ha mer utrymme för att gå runt mellan grupperna gjorde vi några ”öar” med bord, med 4-6 sittplatser runt dem.

Några av barnen kom tidigt och hjälpte oss att flytta borden och stolarna. Det känns som att barnen gillade den här uppställningen, det är ju så det brukar vara i grundskolan och jag tycker att det ger en mer avslappnad känsla. Dessutom kunde vi snabbt skapa stort tomt utrymme i mitten av rummet för en aktivitet i slutet av lektionen.

Introduktion till scheman

Målet med lektionen var att introducera schemaritande i problemlösning. Den idén har vi gått igenom med årskurs 5-6, men nu behövde vi ta ner nivån något för att även de minsta barnen skulle förstå vitsen med tekniken.

Jag tycker om att börja lektionerna med en lekövning, så att alla kan komma igång och få en känsla för dagens tema. Denna gång var det dock svårt att göra övningar i form av spel, det vill säga, det fanns inget uppenbart mål för eleverna. Men de gjorde uppgifterna så som de blivit ombedda att göra och fick hum om dagens tema ändå. Följande fick de göra:

Varje grupp fick två papper. Första pappret skulle de riva sönder i några bitar (så många som de var i gruppen, det vill säga 3-6). Varje person skulle ta en lapp och skriva sitt namn på lappen. Sedan skulle de skrynkla lappen, lägga den i en hög och sedan dra en slumpvis annan lapp. På så sätt skulle varje barn få någon annans namn. På det andra pappret skulle de rita ett schema över vem som fick vems namn.

I den andra övningen skulle de sitta i grupper om 5-6 personer. Barnen skulle blunda och sträcka ut båda sina händer mot mitten. Sedan skulle de ta tag i någon annans hand med vänsterhanden, samt med högerhanden. När alla är klara får man titta igen. Sitter alla ihop nu? Om inte, vilka sitter ihop, vilka sitter inte ihop? Här behövde inte barnen rita, utan bara säga svaren högt.

Det blev lite förvirring över en andra uppgiften, då jag först bad dem att gissa ifall alla satt ihop eller inte när de fortfarande blundade. Vissa grupper kunde ge en gissning, vissa inte. Jag tror att de behöver ha lekt leken några gånger och känna igen situationen för att börja komma på strategier för att testa om de utgör en sammanhängande graf eller inte. Men denna lek var ny för dem och målet med leken var som sagt ganska diffus.

Efter att alla grupper hade testat att göra scheman på sig själva gick vi igenom allas ritningar från första övningen på tavlan. Vissa fick en triangel, vissa fick cirkel och vissa mer avancerade figurer. Vi kom överens om att en cirkel med tre personer är egentligen samma schema som en triangel. Barnen kunde då förstå att en cirkel med fyra personer är samma som en kvadrat. Och att en kvadrat kan ritas på ett annat sätt (som en ”åtta”/”timglas”). Jag försökte poängtera att det inte formen som räknas, utan vem som faktiskt fick vems namn. Detta motsvarar grafisomorfismer i matematiken och det är roligt att introducera isomorfismer till barnen i så tidig ålder och att de verkar förstå.

Grafer

Som vanligt fick eleverna försöka lösa uppgifter i grupper, men denna gång var det naturligt att grupperna blev lite större (på grund av hur gruppen satt i en ring runt ett par bord). Det gjorde troligen så att klassen löste uppgifterna lite fortare än vad de annars skulle ha gjort. Vissa grupper fick en extrauppgift när de var helt klara (en extra svår bild att rita enligt reglerna i uppgift 3).

Under varje uppgift skriver jag några diskussioner jag haft med grupperna.

1. Några barn gick på en picknick. En vuxen ritade av dem på en bild där varje barn blev en liten cirkel. Sedan ritade han ut pilar, som om varje pojke skulle peka på sina systrar. Så här så det ut:

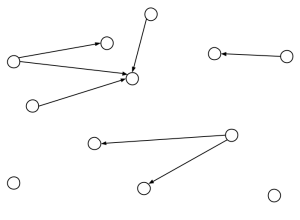
syskon

(a) Vilka barn är säkerligen flickor? Markera dem med ett kryss.
(b) Är det några pilar som den vuxna säkerligen glömde bort att rita ut?

Lärare (ser hur eleverna har ritat): Hur vet ni av de överkryssade är flickor?
Elever: Det är de som man pekade på.
Lärare (ser att inga nya pilar är utsatta): Kan man inte veta något mer, någon som skulle ha pekat på sin syster? Vilka vet man är syskon?
Elever visar på en större grupp, men ibland visar (gissar?) helt fel också.
Lärare (när elever visar fel): Det här kan man inte veta säkert. De kan ha varit syskon, men också är det möjligt att de inte är det. Markera bara det som är helt säkert.

2. Harry Potter vet hur man omvandlar en padda till en prinsessa, en svamp till en
padda och ett päron, ett päron till ett äpple, en äppelskrutt till en kattunge och en
igelkott, en kattunge till ett päron eller ett äpple, en igelkott till ett päron, ett äpple
kan han dock bara omvandla till en äppelskrutt. Just nu har han bara ett äpple. Kan
han omvandla det till en prinsessa?

Elever: Det är svårt att se. Vi lyckas inte..
Lärare: Rita ett schema över vad Harry Potter kan göra. Då kan ni lättare se om svaret är ”ja” eller ”nej”.
Elever: Ahaa, kan svaret alltså vara ”nej”!?

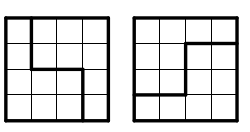
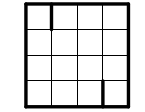
3. Vilken av följande bilder går att rita utan att släppa pennan från pappret? Vilken går inte att rita på det sättet? Det är inte tillåtet att dra samma sträcka flera gånger.

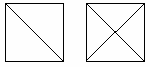
tavlor

Elever: Så här gjorde vi på den första. På den andra går det bara om man ritar ”ett tak”.
Lärare: Nu finns det inget ”tak” på den andra. Varför är det så att det inte går att rita? Man kanske kan börja i mitten?
Elever: Kanske… (prövar)… nä, det går inte att börja i mitten heller.

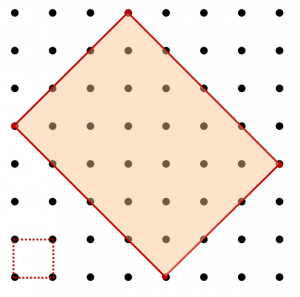
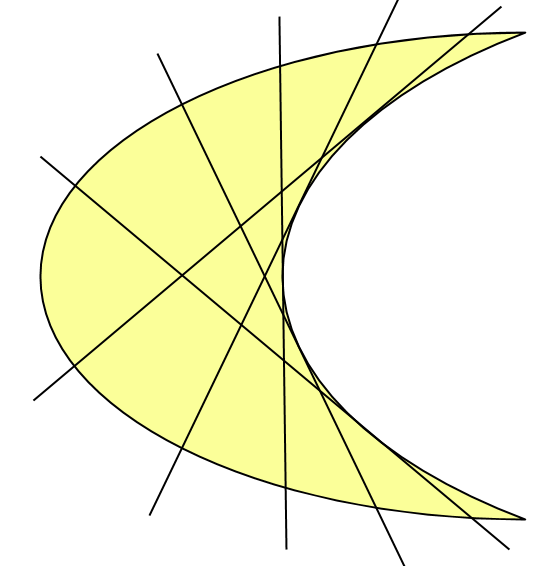
4. Går att rita följande figur utan att lyfta pennan från pappret med samma regler som innan?

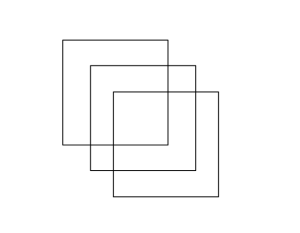
kvadrater

Elev: Jag lyckades! Men jag kommer inte ihåg hur jag gjorde… Vänta så ska jag visa hur man gör (ritar igen).
Lärare: Japp!

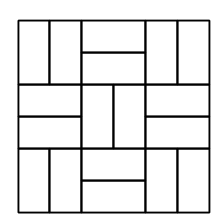
5. Hitta på en figur som består av 8 linjer som inte går att rita enligt reglerna ovan.

Elever: Den här går inte.
Lärare: Består den verkligen av 8 linjer?
Elever: Ah, justja…

Ladda ner uppgifterna för utskrift

 

Genomgång

När de flesta av eleverna var klara med uppgifterna gick vi igenom dem på tavlan.

1. På den första uppgiften ritade jag upp situationen och pekade på cirklarna en i taget samtidigt som jag frågade ”ska det vara ett kryss där?” Då svarade eleverna unisont ”ja” eller ”nej”, förutom i fallen då cirklarna stod ensamma. Där är man faktiskt inte säker. Det skulle kunna vara ett ensambarn och man vet inte huruvida det är en pojke eller en flicka.

Sedan fick några elever komma fram och rita ut pilarna som saknades. Jag sade att halvsyskon inte förekommer i den här uppgiften, fast jag tror egentligen det inte var någon som frågade det heller.

2. Uppgiften om Harry Potter löste eleverna på lite olika sätt. Någon utgick från slutet och kunde motivera svaret ”nej” genom att säga att det inte går att få svamp på något sätt och man måste ha en svamp för att senare få en prinsessa.

Jag ritade ändå upp schemat med pilar över vad man kunde få ur vad, så att det blev klart att det fanns två åtskilda system och man kunde se direkt att det inte gick att gå med pilar mellan dem. Fördelen med den lösningen är att man kan svara på fler frågor än just den som ställs i uppgiften, t.ex. att man inte kan omvandla ett päron till en padda heller.

3. Vi ritade upp den första figuren på tavlan och kom fram till att den andra inte gick (utan att egentligen bevisa det). Jag frågade eleverna var det gick att börja (i vilken punkt) för att rita den första figuren. Efter lite testning kom vi fram till att bara två punkter gick att starta i för att få en korrekt väg.

4. Efter att en elev ritade upp vägen i tre kvadrater-uppgiften ställde jag samma fråga. Vilka punkter gick att starta på eller snarare, vilka punkter går det inte att starta på? Dock när någon elev pekade ut en ”omöjlig” punkt, så visade jag hur man kunde starta i den och rita upp figuren enligt reglerna. Till slut avslöjade jag att det faktiskt gick att starta i vilken punkt som helst.

Vi gick inte igenom teorin om Eulerstigar och hörn med udda/jämn grad, men eleverna är nu mottagliga för den idén efter att ha fått känna på sådana uppgifter.

5. Många grupper fick komma fram till tavlan samtidigt och rita upp sina grafer. Jag ringade in de som var korrekta (bestod av 8 linjer och var omöjliga att rita enligt reglerna), vilket de flesta var.

Efter genomgången tog vi en välbehövd rast. Enligt schemat skulle vi ha lekt knutleken, men jag senarelade den.

Julnötter

Många barn frågade vad ”julnötter” vad för något, eftersom de inte hade träffat på ordet ”nötter” i betydelsen ”kluringar”. Jag tror att vi fick den frågan från alla grupper :)

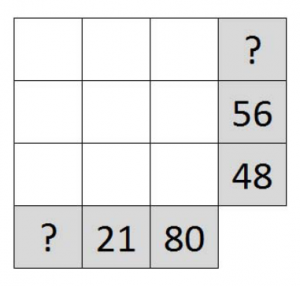
1. Erik var ute och julhandlade. 1/10 av alla sina pengar spenderade han på nötter, 2/5 på kakor och 1/2 på praliner. Hur mycket pengar hade Erik kvar efter att han hade handlat?

Elever: Hur ska man tänka här?
Lärare: Till att börja med, testa vad som skulle ha hänt om Erik hade 10 kronor från början.
Elever (efter att ha räknat): Då skulle han få 0 kronor kvar.
Lärare: Vad skulle hända om han hade 100 kronor från början? 150?
Elever räknar…
Lärare: Ni kan testa att rita upp delarna om det är svårt att räkna.

2. Det finns två timglas som kan mäta 7 respektive 11 minuter. Julgröten måste kokas i exakt 15 minuter. Hur kan man mäta denna tid med hjälp av endast timglasen? Försök att vända timglasen så få gånger som möjligt.

Elever: Hur funkar det här? Vi kommer inte på hur man ska göra.
Lärare: Vi har timglas så att vi kan mäta 7 minuter och vi kan mäta 11 minuter. Kan ni komma på hur man skulle mäta 18 minuter?
Eleverna kommer på hur man gör.
Lärare: 14 minuter då?
Eleverna berättar hur man gör.
Lärare: Försök att komma på ett sätt att mäta 4 minuter.
Efter ett tag kommer en av eleverna i gruppen på hur man gör. Då ber jag att förklara lösningen till de andra gruppen. Efter det brukar någon i gruppen eller samma elev komma på hur man gör för att mäta upp 15 minuter.

3. Har du någonsin gjort girlanger utav gubbar till julgranen? Nedan ser du hur du kan göra en girlang av snögubbar (eller ljus), men hur gör man för att klippa ut en girlang med varannan snögubbe, vartannat ljus?

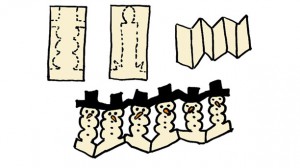
snogubbe

Jag såg endast 1-2 grupper börja på den här uppgiften, eftersom vi hade så lite tid till julnötterna (och de var svåra). Men åtminstone en grupp lyckades göra girlangen.

Ladda ner uppgifterna för utskrift

 

Knutleken

I slutet av lektionen plockade vi bort borden och stolarna i mitten för att göra ett stort tomt utrymme för knutleken. Alla, både eleverna och lärarna, ställde sig i en ring. Vi gjorde samma sak som i början av lektionen, fast i helklass: Alla blundade, sträckte fram två händer och gick mot mitten. Jag hjälpte till när händerna skulle ta tag i varandra, så att alla händer fick en annan och så att inga tre händer möttes. Sedan fick alla titta igen och nu var det meningen att man skulle trassla upp ”knuten” utan att släppa händerna från varandra. Såklart kunde det bli så att flera separata ringar bildades, vilket några av eleverna förutspådde och vilket också hände. Också kunde det hända att några deltagare stod bak-och-fram i slutet, bara för att slutresultatet skulle bli en ring.

Det är faktiskt inte givet att knuten går upp, men oftast gör den det. I vårt fall hade vi en liten ring på två personer som lösgjorde sig i början, samt två större ringar som var fästa i varandra.

Efter att vi var klara skulle eleverna fylla i en liten utvärdering, men så fort de hade gjort det ville de leka knutleken igen. Det gjorde de även efter att lektionen var slut. Jag håller med dem om att det är en kul lek :)

Utvärdering

Precis som i mellanstadiet fick eleverna svara på följande frågor:

Vad har varit roligast att göra på Matteklubben?

Vad har varit minst roligt att göra på Matteklubben?

Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):

1 2 3 4 5

Vill du fortsätta gå på Matteklubben nästa termin (ringa in):

Ja Nej Kanske

Resultatet av utvärderingarna

Efter varje svarsalternativ står det hur många elever hade svarat så. Det märks vilken aktivitet föregick utvärderingen :)

Vad har varit roligast att göra på Matteklubben?

– Lösa uppgifter tillsammans

– Mattekluringar 2 – det borde vara lite svårare och lättare beroende på vilka frågor det är.

– Knutleken 3

– Att man fick vara i grupper och räkna tillsammans 4

– Vet ej

– Allt! Bäst i världen!

– Mattelekarna 4

– Mera matte, mindre raster

– Att klippa rubiks kub

– Att alla uppgifter är lagom svåra

– Goda mackor

Vad har varit minst roligt att göra på Matteklubben?

– Sallad på mackorna

– Vet inte 4

– Vissa uppgifter är svåra!

– Genomgångarna fast de var också roliga

– Att sitta och vänta

– Bara mattelekarna var roliga – minst roligt var allting annat 2

– Kortare genomgångar 3

– För korta raster 2

– Inget 3

– Julnötter

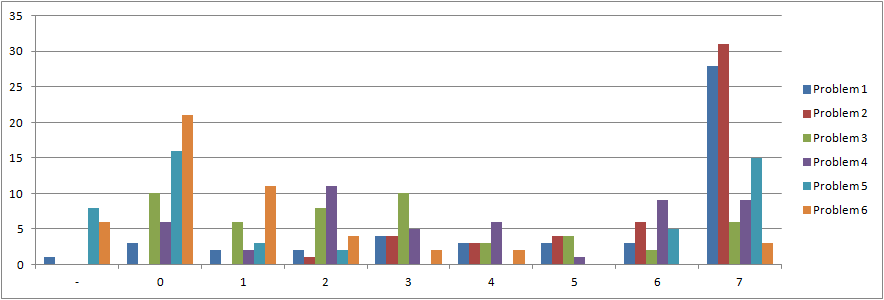
Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):
Betyg 1: 0
Betyg 2: 0
Betyg 3: 9
Betyg 4: 5
Betyg 5: 5

Vill du fortsätta gå på Matteklubben nästa termin?
Ja: 11
Nej: 1
Kanske: 7

Tankar efter terminen

Det märks att de minsta barnen tyckte att det var roligt att gå på Matteklubben, men kanske var det roligast just att ”leka” med matte. Vi har försökt att blanda lek och allvar, speciellt på de senaste två gångerna och det ämnar vi att göra även nästa termin. Möjligen blir det lättare att göra lektionen tillräckligt varierande för att de yngsta barnen ska orka med, då vi kommer att ha 1,5h-lektioner i vår, något kortare än i höstas. Kanske finns det en poäng i att ha någon speciell aktivitet på rasten. På så vis förlorar vi inte så mycket på att göra rasten längre, och barnen får samtidigt samarbeta på ett mer avslappnat sätt och lära känna varandra.

Då matteklubben fortsätter hela 2015 kan jag nu planera ett löpande program istället för att ta enskilda teman. Nu när jag har bättre koll på barnen (och med mindre grupper) vore det kanske möjligt att följa enstaka barnens utveckling.

Har du tips på rastaktiviteter/lekar med matematisk vinkel som passar bra att göra i den här gruppen, kommentera gärna här nedan!

Fjärde träffen med Matteklubben, åk 5-6

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen, andra träffen och tredje träffen innan du läser vidare.

Besök av Uppsalas Nya Tidning

Den fjärde gången fick vi lite halvt oväntat ett besök från Uppsalas Nya Tidning. De kom för att skriva en artikel om Matteklubben i och med att det hade blivit klart att satsningen skulle fortsätta under 2015. Tyvärr innebar det att jag behövde vara ifrån lektionen lite för att svara på journalisternas frågor. Men trots en hastig intervju blev artikeln ganska bra i alla fall! Enda felet de gjorde var att formulera läxan på ett oförståeligt sätt.

UNT: Matteklubben på Ånström gör succé

Det stod ”Uppgiften handlar om att räkna ut om det går att förflytta sig mellan våning ett och två med hiss i ett 100 våningshus om bara knapparna för våning sju och nio fungerar.” Just det där sista med knapparna vore ganska konstigt, utan uppgiften ska formuleras så som det står i läxan.

Hemuppgifterna

I den första hemuppgiften fick eleverna använda sig av knapparna +7 och -9 för att röra sig mellan våningarna. Många hade hunnit tänka på uppgiften redan på den föregående lektionen så att det fanns flera olika idéer. Den mest intressanta diskussionen uppstod när vi skulle förklara varför det går att ta sig från vilken våning som helst till vilken annan våning som helst med hjälp av dessa knappar.

Någon hade en lösning som använde sig av modulo 7 (förstås utan att dessa ord yttrades), det vill säga att först ta sig till en våning som ger samma rest modulo 7 som målvåningen och sedan åka uppåt sju steg i taget (det här gäller för stora målvåningsnummer). En annan hade förklaringen om att strategin för att ta oss upp en våning egentligen kan varieras genom att man byter på knappordningen. Vi kan alltid trycka på knapparna på så sätt att vi slipper åka utanför våningarna och till slut tar oss en våning upp eller ner, vad vi nu behöver.

Det var härligt att se att några elever hade intuion för dessa ganska så abstrakta idéer som moduloräkning och kommutativitet och deras användbarhet.

Den andra uppgiften handlade om hästarna på schackbrädet. Medelst en dialog med eleverna visade jag hur uppgiften kunde lösas med hjälp av en graf. Uppgiften är typisk på det sättet att det är lätt att förstå varför det inte går men svårt att förklara varför. Med en graf av möjliga hästförflyttningar blir det mycket lättare att se och förklara varför det inte kan gå.

Blandat

Den största delen av lektionen togs upp av blandade uppgifter som eleverna löste själva eller i par. De börjar bli väldigt bekanta vid sådana problemlösningssessioner, vilket betyder att vi lärare knappt behöver lägga någon tid på organisation eller disciplin. Vi kan istället snabbt besöka alla eleverna, lyssna på dem och ställa ledande frågor om det behövs.

Under varje uppgift skriver jag ner diskussionerna som jag hann ha med några av eleverna.

1. Shrek hade en stor bit tvål i form av ett rätblock. Efter att han hade duschat 7 gånger blev biten hälften så lång, hälften så bred samt hälften så hög som den var i början. För hur många duschar till räcker den tvålbiten som är kvar?

Elever: Det är svårt att veta hur det ser ut. (De har svårt för att rita 3D-bilder.)
Lärare: Försök att rita vad som skulle hända med en rektangel först. Sedan försök att rita rätblocket.

Elever: Den minskar fyra gånger (visar upp hur de har gjort för en rektangel och säger att det är samma för rätblocket). Sedan vet vi inte hur vi ska räkna.
Lärare: Det här stämmer om tvålen hade varit platt. Men den har en volym. Minskar den inte ännu mer om den också blir mindre på bredden?

2. Hur många tresiffriga tal finns, där alla siffror är olika?

Elever: Vi skrev upp alla sådana tal som börjar med siffran 1. Eller snarare, vi skrev de som börjar med 10.. och det blev åtta stycken. Det blir åtta sådana rader för tal som börjar med 1, så 8*8 = 64 tal. Men första siffran kan väljas som vilken som helst utav 9, så totalt 64*9 = 576 sätt.
Lärare: Ja, det verkar rätt. (Märker felet sedan vid genomgången.) Varför blir det förresten åtta rader?
Elever: (Räknar…) 10, 12, 13, 14, 15, 16, 17, 18, 19 (får ”åtta” ett par gånger, men till slut får ”nio”).

3. Hur stor area har den ifyllda rektangeln på bilden? Ange arean i antalet rutor.
area_rektangel

Elev: Jag delade upp figuren i halvrutor och räknade alla de inuti bilden. Det blev 24.
Lärare: Ja, precis, så kan man göra!

Elever: På ett sätt fick vi 24, men när vi tittar på den som en rektangel så kan man dela upp den i 3*4 = 12 rutor (visar uppdelningen). Varför blir det annat svar?
Lärare: Det stämmer att man delar upp den i 12 rutor, men är det verkligen lika stora rutor som de ursprungliga? Hur var det nu man räknade ut arean på en ”stor” ruta? (Syftar på diskussion av hemuppgiften på den tredje träffen.)
Elever: Ah, de är större ja. De är två rutor stora, alltså är arean 12*2 = 24!

4. Emil plockar svarta och röda kort från en låda och lägger dem i två prydliga högar. Det är förbjudet att lägga kort av samma färg på varandra. Det tionde och det elfte kortet som Emil lägger ut är röda, det tjugofemte är svart. Vilken färg har det tjugosjätte kortet?

Elever: Om han lägger röd-svart-röd-svart och så vidare (på samma hög) från och med det tolfte kortet, så kommer det tjugofemte kortet vara svart och det tjugosjätte vara rött.
Lärare: Men om man skulle lägga korten på något annat sätt, kommer det tjugosjätte kortet fortfarande garanterat vara rött?
Elever: Ahaa, det är det som är frågan…

5. I Sifferlandet finns 9 städer som heter 1, 2, 3, 4, 5, 6, 7, 8 och 9. En turist upptäckte att det finns flyg mellan två städer bara om det tvåsiffriga talet som bildas av stadsnamnen är delbart med 3. Lista alla städer som man kan komma till från staden 1.

Här hann jag inte ha dialog med någon, men i efterhand fick jag se att både vissa lärare och elever var osäkra på om man fick mellanlanda. I gemensamma klassdiskussionen förtydligade vi det och gjorde klart uppgiften.

Ladda ner uppgifterna för utskrift

 

Olika lärare leder diskussionen

Efter den rätt så långa problemlösningssessionen hade vi en paus och sedan drog vi igång genomgången.

Redan i planeringsfasen bestämde vi att olika lärare skulle ta genomgången av varje uppgift. Så fem personer fick var sin uppgift. Det var roligt att se hur alla lärare på ett sätt var lika (frågade eleverna ungefär lika mycket som jag, ställde ledande frågor etc.), men på ett annat sätt också olika. Ingen lärare skulle ju leda redovisningen exakt likadant eller säga exakt samma ord. Jag tror att det är väldigt nyttigt, då mitt sätt att redovisa kanske tilltalar vissa elever, men inte alla. Andra lärare är helt enkelt andra bra förebilder och ju fler olika man får se desto bättre.

Samtidigt kunde jag sätta mig längst bak i klassrummet och se hur det hela såg ut från elevernas sida. Jag försökte också föregå med gott exempel och ställa frågor (som kunde verka dumma) om redovisningen tills jag förstod. Det vill säga, jag spelade inte med, utan jag förstod verkligen inte vissa saker och ställde frågor tills en av lärarna gjorde sakerna klara för mig. Det går inte trycka för mycket på att vi är på Matteklubben för att förstå och inte för att visa oss smarta inför varandra. Det finns inget skam i att inte förstå! Det hjälper ju den som förklarar att bli bättre i just konsten att förklara.

Symmetri

Genomgången tog rätt så lång tid, så den tematiska problemlösningsdelen blev rätt så kort. Några av eleverna påstod att de hade löst allting och fick därför extrauppgifter eller fyllde i utvärderingen tidigare. Vid närmare anblick såg jag att eleverna hade förhastat sig genom uppgifterna, missförstått några och bara trott att de hade löst det.

Nedan skriver jag några sätt som jag kunde syna lösningarna på.

1. Skär ett 4×4-rutnät i två identiska delar. Nedan ser du två sätt, som egentligen är ett och samma. Hitta ett annat sätt.

samma_satt

Lärare: Man får endast skära längs med rutgränserna.

2. Observera att i samtliga fall är skärningslinjen symmetrisk kring kvadratens medelpunkt.
Således lönar det sig att rita länkarna två och två i motsatt läge. Börja vid kanten.

borjan

Bestäm vilka punkter som kan vara ändpunkter till en skärningslinje.
Försök att bestämma alla möjliga svar till uppgift 1.

Här var texten lite förvirrande (många svåra ord!), det var svårt för många att se att frågan egentligen kom efter bilden. Det var också svårt att tolka hjälpen för hur man skulle rita skärningslinjen. Jag tog en genomgång med några av eleverna hur man kan rita en sådan rotationssymmetrisk linje för att få en uppdelning.

Lärare: Kan man starta linjen på något annat ställe? Kan man ”gå” med linjen på olika sätt?

3. En kamomill-blomma har 12 kronblad. Under ett drag får man plocka antingen ett eller två intilliggande kronblad. Den som plockar det sista kronbladet vinner. Vem av spelarna, den som börjar eller den andra, kan vinna oavsett hur skicklig motståndaren är?

Lärare: Ni tror att ni vet vem som vinner? Låt oss spela! (Eleven får vara den spelaren, ettan eller tvåan, som de tror vinner.)

Då eleverna ibland trodde att man fick ta bort två blad, även om de inte satt bredvid varandra, gick deras strategi ut på det. Oftast vann jag, då de inte hade tänkt igenom sin strategi ordentligt, även om de hade fattat reglerna.

4. En turist måste promenera från ett tält till en lägereld samt hämta en hink vatten från en flod under promenaden (se bild).
Exakt vilken väg skall turisten välja för att den ska bli så kort som möjligt?

flod_biljard

Den här uppgiften hann jag inte diskutera med någon. Den är svår att formulera på ett bra sätt. Vad menas med ”exakt”? Som matematiker vet man vad som man underförstått kan konstruera (linjer genom givna och erhållna punkter till exempel). Men som barn räcker det kanske bara att rita för hand. Den ungefärliga lösningen blir ju ”bra nog”.

Ladda ner uppgifterna för utskrift

 

Utvärdering

Vi avslutade lektionen och terminen genom att fylla i en liten utvärdering. Följande frågor fick de svara på:

Vad har varit roligast att göra på Matteklubben?

Vad har varit minst roligt att göra på Matteklubben?

Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):

1 2 3 4 5

Vill du fortsätta gå på Matteklubben nästa termin (ringa in):

Ja Nej Kanske

Föräldrarna fick fylla i en utvärdering på nätet, men där har jag inte fått se svaren än.

Resultatet av utvärderingarna

Efter varje svarsalternativ står det hur många elever hade svarat så.

Vad har varit roligast att göra på Matteklubben?

– Tävling 14

– Lyckas med att lösa svårare uppgifter och ha rätt

– Att lära mig nya sätt att lösa uppgifter 2

– Bra blandning av olika delar i matten (symmetri, schema mm)

– Samarbetsuppgifter 2

– När man löste ett problem genom att samarbeta med gruppen. Då blev vi stolta

– Problemlösning 4

– Att äta (3) och att göra uppgifter i små grupper 2

– Att vara med kompisar och räkna roliga uppgifter 2

– Lösa kluriga uppgifter 3

– Svår matte 2

– Läxorna/”förhören”

Vad har varit minst roligt att göra på Matteklubben?

– Jobba i större grupper 2

– Långa tråkiga genomgångar och för komplicerade uppgifter

– Väldigt långa genomgångar 4

– Svåra uppgifter/uppgifter man inte förstod 3

– Lätta uppgifter 2

– Att det har varit så långt. Det kunde varit lite kortare

– Att inte få redovisa varje gång

– Inget/vet inte 9

– Att vissa fjantar sig under lektionerna

– Tävlingen – jag blir stressad …

– Göra tråkiga uppgifter

– Läxorna

– Kort rast

– Att ha fel 2

– Tävla och jobba

Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):
Betyg 1: 0
Betyg 2: 1
Betyg 3: 10
Betyg 4: 19
Betyg 5: 3

Vill du fortsätta gå på Matteklubben nästa termin?
Ja: 20
Nej: 0
Kanske: 13

Tankar efter terminen

Spontana tankar jag har efter de här fyra träffarna och efter att ha sett utvärderingarna är att det blev en väldigt lyckad start!

Såklart har inte allting varit perfekt, till exempel har de långa genomgångarna kanske inte gett så mycket som vi trodde. En idé jag får är att ha genomgångarna i små grupper, att man turas om att presentera uppgifterna inför 4-5 andra. Något att experimentera med nästa termin!

En annan tydlig sak är att eleverna älskade att tävla. Jag har tidigare skrivit om varför tävlingar engagerar så och får elever att prestera på topp. Nästa termin planerar jag att ha små tävlingar kanske var tredje träff. Om möjligt hoppas jag att vi kan få besök av en mattegrupp från en annan kommun, så att våra elever kan tävla mot varandra.

Kanske behöver nivån på uppgifterna sänkas något, jag har lätt för att dra upp svårighetsgraden onödigt mycket. Jag hoppas att andra lärare kommer kunna hjälpa mig med det, de har nu fått erfarenhet och uppfattning om vad som är lagom för högpresterande elever i den här åldern.

Jag vill tacka eleverna, föräldrarna, de andra lärarna, kommunen och matteinstitutionen för jätteroliga fyra träffar, och ser fram emot att fortsätta nästa termin!

Korstal 2014

Korstal 2014

Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.

korstal2014

Ladda ner för utskrift

Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är likadana
7. Ett kubtal delbar med lodrätt 3
9. Ett tal bestående av siffror som är kvadrattal, där alla sådana siffror förekommer
11. Vågrätt 1 plus vågrätt 5 minus lodrätt 1

Lodrätt:
1. Antalet positiva tvåsiffriga tal
2. Ett palindromårtal i det förflutna
3. En delare till lodrätt 2
4. Vågrätt 1 minus vågrätt 5
5. Vågrätt 1 gånger vågrätt 5
6. Vågrätt 9 plus lodrätt 5
8. En tvåpotens minus lodrätt 1
10. Delbart med lodrätt 3

Ett kvadrattal är kvadrat av ett heltal. Ett kubtal är kub (tredjepotens) av ett heltal. Ett palindromtal är ett tal som ser likadant ut fram- som baklänges. En tvåpotens är 2 multiplicerat med sig själv några gånger (även 1 och 2 räknas som tvåpotenser). Med delbart med N menas att det går att jämnt dela med talet N. Med delare till N menas att N går att dela jämnt på det talet.

Visa lösningen

Summan av produkter

Summan av produkter

För varje tresiffrigt tal skrev man upp produkten av dess siffror. Sedan räknade man ut summan av alla dessa produkter. Vad fick man för tal? (Om en av siffrorna i talet är 0, så är sifferprodukten såklart 0 också).

Visa lösningen

Månskäran

Månskäran

I hur många delar kan man som mest dela upp månskäran med hjälp av 5 raka linjer? Delarna får inte arrangeras om mellan skärningarna.

manbage

Visa lösningen

Bråkdelar

Bråkdelar

En speciell miniräknare har bara en knapp. Genom att trycka på den ökar man talet på skärmen med dess bråkdel (t.ex. kan man få 6/7 från 3/7 då 3/7 + 3/7 = 6/7 eller 4,6 från 3,8 då 3,8 + 0,8 = 4,6). Från början stod ett positivt tal som är mindre än 1 på skärmen. Efter tio knapptryckningar fick man talet 10. Vilket tal stod på skärmen från början?

Visa lösningen

Shejkens slott

Shejkens slott

En shejk har ett slott som ser ut som en 6×6-kvadrat indelad i 1×1-rum. I mitten av varje vägg finns en dörr mellan rummen. Shejken ger order till hovbyggaren att ta bort några väggar, så att det bara bildas rum av storleken 2×1, inga nya dörrar tillkommer och att man som mest ska behöva gå genom N dörrar för att gå från ett rum till ett annat.

Vilket är det minsta möjliga värdet på N så att alla shejkens önskemål fortfarande går att uppfylla?

6x6

Visa lösningen

Virusattacker

Virusattacker

Datorerna med nummer från 1 till 100 är kopplade i en kedja: 1 är kopplad till 2, 2 kopplad till 3, osv., 100 är kopplad till 1. Några hackers har förberett hundra olika virus, som de har gett nummer från 1 till 100 och sedan slumpar de i vilken ordning de ska skicka dem. De skickar varje virus till en dator med samma nummer som viruset (t.ex. om virus nummer 32 står först i kön så skickas det till dator nummer 32). Virusen skickas inte vid några regelbundna tider, utan det kan ske lite när som helst.

Om ett virus kommer till en osmittad dator, så smittas datorn och viruset fortsätter till nästa dator i kedjan. Så fortsätter viruset (från dator 100 kommer den till dator 1) tills det kommer till en dator som redan är smittad. Då försvinner det viruset och datorn den kom till blir osmittad igen. Det blir aldrig så att två virus kommer samtidigt till en och samma dator.

Hur många datorer förblir smittade i slutändan av dessa hundra virus?

Visa lösningen

© 2009-2024 Mattebloggen