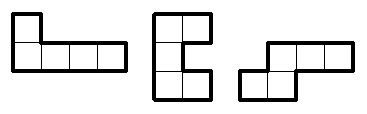symmetri

Fjärde träffen med Matteklubben, åk 5-6

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen, andra träffen och tredje träffen innan du läser vidare.

Besök av Uppsalas Nya Tidning

Den fjärde gången fick vi lite halvt oväntat ett besök från Uppsalas Nya Tidning. De kom för att skriva en artikel om Matteklubben i och med att det hade blivit klart att satsningen skulle fortsätta under 2015. Tyvärr innebar det att jag behövde vara ifrån lektionen lite för att svara på journalisternas frågor. Men trots en hastig intervju blev artikeln ganska bra i alla fall! Enda felet de gjorde var att formulera läxan på ett oförståeligt sätt.

UNT: Matteklubben på Ånström gör succé

Det stod ”Uppgiften handlar om att räkna ut om det går att förflytta sig mellan våning ett och två med hiss i ett 100 våningshus om bara knapparna för våning sju och nio fungerar.” Just det där sista med knapparna vore ganska konstigt, utan uppgiften ska formuleras så som det står i läxan.

Hemuppgifterna

I den första hemuppgiften fick eleverna använda sig av knapparna +7 och -9 för att röra sig mellan våningarna. Många hade hunnit tänka på uppgiften redan på den föregående lektionen så att det fanns flera olika idéer. Den mest intressanta diskussionen uppstod när vi skulle förklara varför det går att ta sig från vilken våning som helst till vilken annan våning som helst med hjälp av dessa knappar.

Någon hade en lösning som använde sig av modulo 7 (förstås utan att dessa ord yttrades), det vill säga att först ta sig till en våning som ger samma rest modulo 7 som målvåningen och sedan åka uppåt sju steg i taget (det här gäller för stora målvåningsnummer). En annan hade förklaringen om att strategin för att ta oss upp en våning egentligen kan varieras genom att man byter på knappordningen. Vi kan alltid trycka på knapparna på så sätt att vi slipper åka utanför våningarna och till slut tar oss en våning upp eller ner, vad vi nu behöver.

Det var härligt att se att några elever hade intuion för dessa ganska så abstrakta idéer som moduloräkning och kommutativitet och deras användbarhet.

Den andra uppgiften handlade om hästarna på schackbrädet. Medelst en dialog med eleverna visade jag hur uppgiften kunde lösas med hjälp av en graf. Uppgiften är typisk på det sättet att det är lätt att förstå varför det inte går men svårt att förklara varför. Med en graf av möjliga hästförflyttningar blir det mycket lättare att se och förklara varför det inte kan gå.

Blandat

Den största delen av lektionen togs upp av blandade uppgifter som eleverna löste själva eller i par. De börjar bli väldigt bekanta vid sådana problemlösningssessioner, vilket betyder att vi lärare knappt behöver lägga någon tid på organisation eller disciplin. Vi kan istället snabbt besöka alla eleverna, lyssna på dem och ställa ledande frågor om det behövs.

Under varje uppgift skriver jag ner diskussionerna som jag hann ha med några av eleverna.

1. Shrek hade en stor bit tvål i form av ett rätblock. Efter att han hade duschat 7 gånger blev biten hälften så lång, hälften så bred samt hälften så hög som den var i början. För hur många duschar till räcker den tvålbiten som är kvar?

Elever: Det är svårt att veta hur det ser ut. (De har svårt för att rita 3D-bilder.)
Lärare: Försök att rita vad som skulle hända med en rektangel först. Sedan försök att rita rätblocket.

Elever: Den minskar fyra gånger (visar upp hur de har gjort för en rektangel och säger att det är samma för rätblocket). Sedan vet vi inte hur vi ska räkna.
Lärare: Det här stämmer om tvålen hade varit platt. Men den har en volym. Minskar den inte ännu mer om den också blir mindre på bredden?

2. Hur många tresiffriga tal finns, där alla siffror är olika?

Elever: Vi skrev upp alla sådana tal som börjar med siffran 1. Eller snarare, vi skrev de som börjar med 10.. och det blev åtta stycken. Det blir åtta sådana rader för tal som börjar med 1, så 8*8 = 64 tal. Men första siffran kan väljas som vilken som helst utav 9, så totalt 64*9 = 576 sätt.
Lärare: Ja, det verkar rätt. (Märker felet sedan vid genomgången.) Varför blir det förresten åtta rader?
Elever: (Räknar…) 10, 12, 13, 14, 15, 16, 17, 18, 19 (får ”åtta” ett par gånger, men till slut får ”nio”).

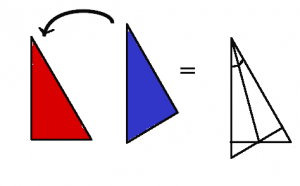
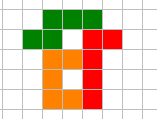
3. Hur stor area har den ifyllda rektangeln på bilden? Ange arean i antalet rutor.
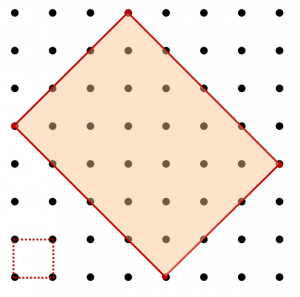
area_rektangel

Elev: Jag delade upp figuren i halvrutor och räknade alla de inuti bilden. Det blev 24.
Lärare: Ja, precis, så kan man göra!

Elever: På ett sätt fick vi 24, men när vi tittar på den som en rektangel så kan man dela upp den i 3*4 = 12 rutor (visar uppdelningen). Varför blir det annat svar?
Lärare: Det stämmer att man delar upp den i 12 rutor, men är det verkligen lika stora rutor som de ursprungliga? Hur var det nu man räknade ut arean på en ”stor” ruta? (Syftar på diskussion av hemuppgiften på den tredje träffen.)
Elever: Ah, de är större ja. De är två rutor stora, alltså är arean 12*2 = 24!

4. Emil plockar svarta och röda kort från en låda och lägger dem i två prydliga högar. Det är förbjudet att lägga kort av samma färg på varandra. Det tionde och det elfte kortet som Emil lägger ut är röda, det tjugofemte är svart. Vilken färg har det tjugosjätte kortet?

Elever: Om han lägger röd-svart-röd-svart och så vidare (på samma hög) från och med det tolfte kortet, så kommer det tjugofemte kortet vara svart och det tjugosjätte vara rött.
Lärare: Men om man skulle lägga korten på något annat sätt, kommer det tjugosjätte kortet fortfarande garanterat vara rött?
Elever: Ahaa, det är det som är frågan…

5. I Sifferlandet finns 9 städer som heter 1, 2, 3, 4, 5, 6, 7, 8 och 9. En turist upptäckte att det finns flyg mellan två städer bara om det tvåsiffriga talet som bildas av stadsnamnen är delbart med 3. Lista alla städer som man kan komma till från staden 1.

Här hann jag inte ha dialog med någon, men i efterhand fick jag se att både vissa lärare och elever var osäkra på om man fick mellanlanda. I gemensamma klassdiskussionen förtydligade vi det och gjorde klart uppgiften.

Ladda ner uppgifterna för utskrift

Olika lärare leder diskussionen

Efter den rätt så långa problemlösningssessionen hade vi en paus och sedan drog vi igång genomgången.

Redan i planeringsfasen bestämde vi att olika lärare skulle ta genomgången av varje uppgift. Så fem personer fick var sin uppgift. Det var roligt att se hur alla lärare på ett sätt var lika (frågade eleverna ungefär lika mycket som jag, ställde ledande frågor etc.), men på ett annat sätt också olika. Ingen lärare skulle ju leda redovisningen exakt likadant eller säga exakt samma ord. Jag tror att det är väldigt nyttigt, då mitt sätt att redovisa kanske tilltalar vissa elever, men inte alla. Andra lärare är helt enkelt andra bra förebilder och ju fler olika man får se desto bättre.

Samtidigt kunde jag sätta mig längst bak i klassrummet och se hur det hela såg ut från elevernas sida. Jag försökte också föregå med gott exempel och ställa frågor (som kunde verka dumma) om redovisningen tills jag förstod. Det vill säga, jag spelade inte med, utan jag förstod verkligen inte vissa saker och ställde frågor tills en av lärarna gjorde sakerna klara för mig. Det går inte trycka för mycket på att vi är på Matteklubben för att förstå och inte för att visa oss smarta inför varandra. Det finns inget skam i att inte förstå! Det hjälper ju den som förklarar att bli bättre i just konsten att förklara.

Genomgången tog rätt så lång tid, så den tematiska problemlösningsdelen blev rätt så kort. Några av eleverna påstod att de hade löst allting och fick därför extrauppgifter eller fyllde i utvärderingen tidigare. Vid närmare anblick såg jag att eleverna hade förhastat sig genom uppgifterna, missförstått några och bara trott att de hade löst det.

Nedan skriver jag några sätt som jag kunde syna lösningarna på.

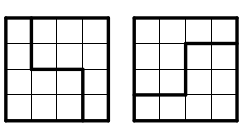
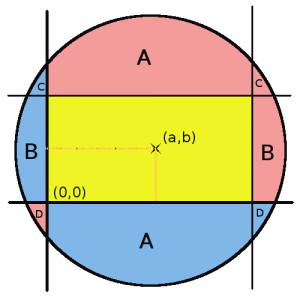
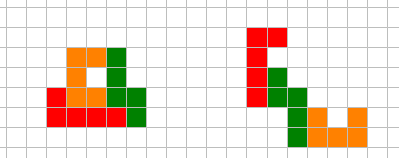
1. Skär ett 4×4-rutnät i två identiska delar. Nedan ser du två sätt, som egentligen är ett och samma. Hitta ett annat sätt.

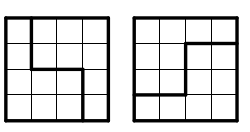
samma_satt

Lärare: Man får endast skära längs med rutgränserna.

2. Observera att i samtliga fall är skärningslinjen symmetrisk kring kvadratens medelpunkt.
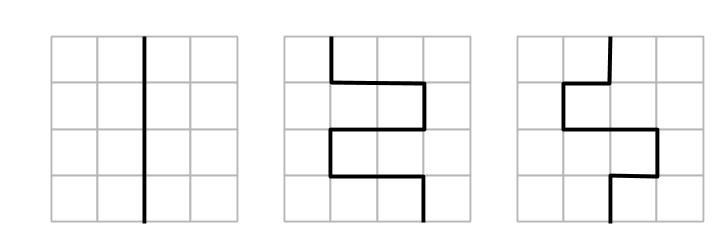
Således lönar det sig att rita länkarna två och två i motsatt läge. Börja vid kanten.

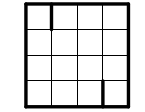
borjan

Bestäm vilka punkter som kan vara ändpunkter till en skärningslinje.
Försök att bestämma alla möjliga svar till uppgift 1.

Här var texten lite förvirrande (många svåra ord!), det var svårt för många att se att frågan egentligen kom efter bilden. Det var också svårt att tolka hjälpen för hur man skulle rita skärningslinjen. Jag tog en genomgång med några av eleverna hur man kan rita en sådan rotationssymmetrisk linje för att få en uppdelning.

Lärare: Kan man starta linjen på något annat ställe? Kan man ”gå” med linjen på olika sätt?

3. En kamomill-blomma har 12 kronblad. Under ett drag får man plocka antingen ett eller två intilliggande kronblad. Den som plockar det sista kronbladet vinner. Vem av spelarna, den som börjar eller den andra, kan vinna oavsett hur skicklig motståndaren är?

Lärare: Ni tror att ni vet vem som vinner? Låt oss spela! (Eleven får vara den spelaren, ettan eller tvåan, som de tror vinner.)

Då eleverna ibland trodde att man fick ta bort två blad, även om de inte satt bredvid varandra, gick deras strategi ut på det. Oftast vann jag, då de inte hade tänkt igenom sin strategi ordentligt, även om de hade fattat reglerna.

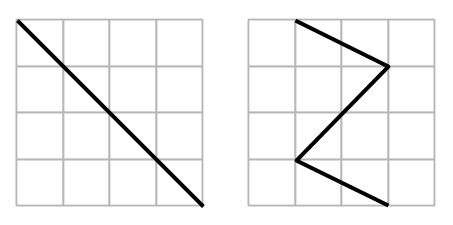
4. En turist måste promenera från ett tält till en lägereld samt hämta en hink vatten från en flod under promenaden (se bild).
Exakt vilken väg skall turisten välja för att den ska bli så kort som möjligt?

flod_biljard

Den här uppgiften hann jag inte diskutera med någon. Den är svår att formulera på ett bra sätt. Vad menas med ”exakt”? Som matematiker vet man vad som man underförstått kan konstruera (linjer genom givna och erhållna punkter till exempel). Men som barn räcker det kanske bara att rita för hand. Den ungefärliga lösningen blir ju ”bra nog”.

Ladda ner uppgifterna för utskrift

Utvärdering

Vi avslutade lektionen och terminen genom att fylla i en liten utvärdering. Följande frågor fick de svara på:

Vad har varit roligast att göra på Matteklubben?

Vad har varit minst roligt att göra på Matteklubben?

Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):

1 2 3 4 5

Vill du fortsätta gå på Matteklubben nästa termin (ringa in):

Ja Nej Kanske

Föräldrarna fick fylla i en utvärdering på nätet, men där har jag inte fått se svaren än.

Resultatet av utvärderingarna

Efter varje svarsalternativ står det hur många elever hade svarat så.

Vad har varit roligast att göra på Matteklubben?

– Tävling 14

– Lyckas med att lösa svårare uppgifter och ha rätt

– Att lära mig nya sätt att lösa uppgifter 2

– Bra blandning av olika delar i matten (symmetri, schema mm)

– Samarbetsuppgifter 2

– När man löste ett problem genom att samarbeta med gruppen. Då blev vi stolta

– Problemlösning 4

– Att äta (3) och att göra uppgifter i små grupper 2

– Att vara med kompisar och räkna roliga uppgifter 2

– Lösa kluriga uppgifter 3

– Svår matte 2

– Läxorna/”förhören”

Vad har varit minst roligt att göra på Matteklubben?

– Jobba i större grupper 2

– Långa tråkiga genomgångar och för komplicerade uppgifter

– Väldigt långa genomgångar 4

– Svåra uppgifter/uppgifter man inte förstod 3

– Lätta uppgifter 2

– Att det har varit så långt. Det kunde varit lite kortare

– Att inte få redovisa varje gång

– Inget/vet inte 9

– Att vissa fjantar sig under lektionerna

– Tävlingen – jag blir stressad …

– Göra tråkiga uppgifter

– Läxorna

– Kort rast

– Att ha fel 2

– Tävla och jobba

Ge dig själv betyg 1-5 (5 är högst) beroende på hur flitig du har varit med att lösa problemen (ringa in):
Betyg 1: 0
Betyg 2: 1
Betyg 3: 10
Betyg 4: 19
Betyg 5: 3

Vill du fortsätta gå på Matteklubben nästa termin?
Ja: 20
Nej: 0
Kanske: 13

Tankar efter terminen

Spontana tankar jag har efter de här fyra träffarna och efter att ha sett utvärderingarna är att det blev en väldigt lyckad start!

Såklart har inte allting varit perfekt, till exempel har de långa genomgångarna kanske inte gett så mycket som vi trodde. En idé jag får är att ha genomgångarna i små grupper, att man turas om att presentera uppgifterna inför 4-5 andra. Något att experimentera med nästa termin!

En annan tydlig sak är att eleverna älskade att tävla. Jag har tidigare skrivit om varför tävlingar engagerar så och får elever att prestera på topp. Nästa termin planerar jag att ha små tävlingar kanske var tredje träff. Om möjligt hoppas jag att vi kan få besök av en mattegrupp från en annan kommun, så att våra elever kan tävla mot varandra.

Kanske behöver nivån på uppgifterna sänkas något, jag har lätt för att dra upp svårighetsgraden onödigt mycket. Jag hoppas att andra lärare kommer kunna hjälpa mig med det, de har nu fått erfarenhet och uppfattning om vad som är lagom för högpresterande elever i den här åldern.

Jag vill tacka eleverna, föräldrarna, de andra lärarna, kommunen och matteinstitutionen för jätteroliga fyra träffar, och ser fram emot att fortsätta nästa termin!

Tredje träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen och den andra träffen med gruppen.

Från början hade vi tänkt att både ha med en del med blandade problem och en tematisk del. Vi hann dock bara gå igenom blandade problemen. Dock gjorde vi det ordentligt och dessutom fanns det trots allt en röd tråd i de här problemen, även om den inte var uppenbar. Men mer om det senare!

Precis som förra gången var 29 barn och 6 lärare med på träffen.

En lek med frågor

För att barnen skulle lära känna varandra i gruppen (och inte bara känna dem från egna skolan) började vi lektionen med en frågelek. Egentligen är det en matematisk lek, men det är inte helt uppenbart varför.

Reglerna var enkla: jag eller någon annan lärare tänkte på en person i klassrummet. Eleverna skulle ställa ”ja/nej”-frågor till oss för att ta reda på vem det var. Den som räckte upp handen fick chansen att ställa nästa fråga och jag försökte hela tiden välja personer som inte hade ställt någon fråga tidigare.

Men hjälp av frågorna ”Är det en tjej eller en kille?” (varpå jag svarade ”Ja” och frågan ändrades till ”Är den en kille?”), ”Är det jag?”, ”Är det han?”, ”Sitter personen på mittenraden?”, ”Har personen en blå tröja?” etc. kunde barnen gissa rätt person på 11 försök.

Lek i grupper

Nu skulle barnen testa samma lek i grupper om 4-6. Vi gav ut papper för att de skulle anteckna antalet frågor det tog att gissa personen som någon i gruppen tänkte på. På tavlan skrev jag upp gruppernas rekord: ”5 försök, 7 försök, 1 försök(!)…” Möjligen blev fokusen vid att ha så få försök som möjligt för stor, vilket gjorde att barnen ofta chansade just för att kunna gissa personen på ett försök. I snitt blev barnen bättre på att spela spelet, då oftast tog det mycket mindre än 11 försök.

Efter ett en stund pratade vi om vilka frågor som var bra att ställa. Egentligen syftade jag på frågor som ungefär halverar gruppen av misstänkta personer. Men jag formulerade inte, då barnen ändå förstod det intuitivt efter att ha lekt med frågorna.

”Är det en kille?”, ”Är det ett barn?”, ”Sitter personen på mittenraden?”, ”Har personen en långärmad tröja?”, ”Har personen ljust hår?” var några av de riktigt bra exempelfrågor som barnen kom på.

Blandade problem, del 1

Därefter delade vi ut ett blad med fem blandade problem. Det visade sig att problemen absolut inte var för lätta. Alla hade något att klura på, så jag ville inte skynda på processen bara för att hinna med en del till. Istället gjorde vi uppehåll i lösandet, då vi gick igenom de första två problemen och sedan tog vi rast.

Eleverna försöker alltid lösa problemen i ordning och hoppar oftast inte över något problem förrän de känner sig klara eller uttråkade. Nästan alltid har de några idéer på varje uppgift de hunnit börja på, så det finns alltid något att diskutera med varje grupp.

1. a) Hur många tvåsiffriga tal finns det?
b) Hur många tresiffriga tal finns det?

Elever: På a) är svaret 90
Lärare: Hur tänker ni?
Elever: Det är 99 tal som har upp till två siffror, men 1,2,3,4,5,6,7,8,9 är inte tvåsiffriga, dem måste vi ta bort.
Lärare: Japp, och var blir svaret på b)?
Elever: 990 eller.. 989… eller…
Lärare: Försök att räkna på liknande sätt. Hur många tal har upp till tre siffror och hur många måste vi räkna bort?

2. Skär ett 4×4-rutnät i två identiska delar. Försök att finna flera olika sätt. Nedan ser du två sätt, som egentligen är ett och samma:

samma_satt

Elever: Räknas de här (pekar på olika sätt)?
Lärare: Ja, de här är olika, men dessa (pekar på två egentligen likadana sätt) räknas som samma, eftersom man kan vrida bilden så att det ser likadant ut.

I vissa fall tyckte alltså eleverna att alla fyra sätten som här på bilden räknades som samma, i andra fall ansågs det att de räknades som två olika sätt (vänsterbilderna som ett sätt, högerbilderna som ett annat, eftersom de inte gick att vrida om till varandra).

uppdelningar_upprepning

Redovisning, del 1

Några elever fick komma fram och redovisa uppgift 1 (en grupp fick punkt a), den andra punkt b) då vi alltid har många frivilliga som vill fram, så jag försöker att ha framme så många olika personer som möjligt under lektionen).

På punkt b) fanns flera olika sätt att tänka, och gruppen vid tavlan gjorde en väldigt snygg lösning. De tog 1000 tal (1 till 1000), och sedan tog bort 100 (vad jag minnst). Det blir 900. Men 100 ska egentligen räknas med så det blir +1, det vill säga 901. Men 100 ska inte räknas med så det blir -1, det vill säga 900.

På andra uppgiften fick många grupper komma fram (en grupp i taget) och rita upp ett av sina sätt. Det blev totalt omkring 8 sätt, bland annat de här:

uppdelningar

Några av eleverna begränsades inte av tänket ”måste skära längs med rutorna” och gjorde på följande sätt:

uppdelningar_kreativa

Det stod ju trots allt inte i uppgiften att man var tvungen att skära längs med rutorna (för mig var det underförstått). Det kom lite upprörda röster från vissa som tyckte att det inte räknades, och jag försökte säga att det egentligen blev två olika problem som vi löste. Och att dessa kreativa lösningarna räknades när man löste den ena versionen av problemet, men inte den andra.

(Lärdomen är att vara tydligare i uppgiftsformuleringen.)

Jag visade även att man kunde få alla uppdelningar genom att rita en linje som var symmetrisk kring centrum (eller snarare, några barn greppade vad jag var ute efter när jag frågade om uppdelningslinjen betedde sig på något speciellt sätt). Detta kan man säga även om linjer som inte följer rutgränserna.

Blandade problem, del 2

3. Ett litet barn har 3 röda och 2 blå kuber. Alla kuberna har samma storlek. Hur många 5 kuber höga olika torn kan barnet bygga?

Elev: Det finns ju jättemånga sätt! Jag vet inte om orkar rita upp alla.
Lärare: Försökt att göra det på ett strukturerat sätt. Då är det lättare att få översikt och inte glömma bort något sätt.

4. Det finns 60 trästockar, som alla är 3 meter långa, som ska huggas upp i halvmeterlånga delar. Hur många sågningar måste man göra?

Elev: Det är 6 bitar som varje stock delas upp i, således blir det 60*6 = 360 sågningar.
Lärare: Men är det verkligen 6 sågningar per bit? Hur många gånger skulle vi såga för att dela upp en stock i två bitar?
Elever: En..
Lärare: Och i tre bitar?
Elever: Två..
Lärare: Och i fler bitar?
Elever: Aha… (och man ser en aha-upplevelse i deras ansikten), det behövs 5 sågningar per stock, så svaret blir 60*5.

5. En bit föll ur en gammal tidskrift.
Första sidan hade numret 328 och sista hade ett nummer som bestod av samma siffror, men i en annan ordning. Hur många sidor föll ut ur tidskriften?

magazine

Elever: Sista sidan måste vara udda, alltså är det 823.
Lärare: Varför inte 283 då?
Elever: Men det är ju mindre, det ska vara större! Och då är det 823 – 328 = 495 sidor som ramlade ur.

Här blev det långa diskussioner med många av grupperna om vad som är sidor, vad som är blad (två sidor), om svaret verkligen kunde bli ett udda antal sidor och hur man egentligen ska räkna antalet sidor i en bit. Många hade svårt att förstå att man skulle (och varför man skulle) lägga till 1 efter subtraktionen.

Ladda ner uppgifterna för utskrift

Redovisning, del 2

Här hade vi inte så mycket tid kvar, så redovisningen gick ganska snabbt.

För att lättare föreställa sig tornet från uppgift 3 ritade jag upp det:
undervisar

Sedan frågade jag vilket svar alla hade fått och skrev upp förslagen som sades högt: 20, 10, 11. Grupperna fick förklara från sina egna platser hur de fick just det svaret.

Den tydligaste strategin hade gruppen som hade svaret 10 (vilket också var rätt svar): Att först räkna de 4 fallen då en av de blåa kuber är längst ner. Sedan är det 3 fall kvar när en är näst längst ner (nu är det en röd längst ner, eftersom vi redan har betraktat de andra möjligheterna). Fortsätter man så, får man till slut svaret 4 + 3 + 2 + 1 = 10.

Lustigt nog blev inte alla barnen övertygade om svaret, utan en elev envisades med att svaret var 11 (eleven skrev upp alla möjligheter). Vi lärare föreslog att det antagligen fanns två sätt som sammanföll, men eleven stod på sig. Tyvärr hann vi inte kolla på dessa sätt efter lektionen. Men det är imponerande med sådant matematiskt självförtroende! Den finns i mycket mindre grad hos äldre elever.

På uppgiften om stockar fick en elev gå fram till tavlan och redovisa. Men det blev ett tankefel med antalet skärningar per stock, vilket eleven fick till 3. Tillsammans hjälpte klassen till att korrigera antalet sågningar per stock till 5, vilket till slut gav rätt svar.

Två elever kom fram och redovisade uppgiften om sidorna. De motiverade bra och räknade skillnaden rätt, men de behövde också förklara varför det inte bara är skillnaden, utan skillnaden plus ett som ger det rätta antalet sidor. Eleverna förklarade det med att man ”lägger tillbaka” sidan nummer 328.

Vi var tvungna att avbryta på grund av tiden, men jag tror att några hann förstå att det inte är så enkelt som att bara räkna ut skillnaden mellan två tal, när man ska ta reda på hur många tal det är som ligger mellan dem.

Röd tråd genom blandade uppgifter

Det gemensamma tankesättet för uppgifterna 1, 4 och 5 blev just ”effekten +/-1”, som går ut på att man får ett fel svar eller delsvar, som avviker med 1 från det korrekta. Effekten är ett mycket vanligt tankefel som händer de flesta vuxna och dyker också ofta upp i programmering. När man inte stannar upp och tänker efter så kan man tro att det måste ske 6 sågningar för att dela upp ett stock i 6 delar, men det ska vara 5.

En ännu mer generell idé som används vid lösningen av dessa uppgifter är att ha koll på vad man lägger till och vad man tar bort. Till exempel, i uppgift 1 b) kan man lägga till talen 1 till 999, och sedan ta bort talen 1 till 99. Då är det lättare att se att svaret är 999 – 99 = 900. I uppgiften om sidor kan man först räkna med alla sidor från 1 till 823 (823 stycken) och sedan ta bort 1 till 327 (eftersom 328 ska finnas med) och då få 823 – 327 = 496 sidor.

Den andra idén hade svårare att få fäste hos eleverna, möjligen behöver de öva mer på den i framtiden (medelst något lättare uppgifter, som t.ex. nummer 1). Det var också svårare att greppa tankesättet när de jobbade med så pass stora tal som 823 och 328. De hade ingen intuitiv känsla för talen, och sade ofta att skillnaden de emellan var 505 (800 – 300 = 500, 28 – 23 = 5). Jag ska nog vara försiktig med att använda stora tal i uppgifter som går ut på att upptäcka nya idéer.

Känslan efter lektionen

Trots att vi inte hann med temat, kändes lektionen fullständig. Det blev lite variation i och med leken i början av lektionen, vilken kändes uppskattad av eleverna. Trots att vi var lika många som förra gången, så kändes det mycket lugnare än vanligt, kanske för att alla var vana vid arbetssättet vid det här laget.

Bland det bästa med eleverna i åk 2-4 är att de inte håller sig för att säga sanningen. De kan både öppet kritisera och säga lovord. Denna gång blev jag väldigt glad när en av eleverna sade att Matteklubben-dagar var tillsammans med födelsedagen hennes favoritdagar! Sånt blir man glad av att höra och jag hoppas att flera elever känner något liknande.

Jag ser fram emot nästa träff, den sista före Jul, då vi också kommer att ha en liten utvärdering om höstterminen.

Lösningen till problemet för de yngre vecka 38

Mattegåta

Jon-Erik har en triangel utan några markeringar, som är gjord av plast. Triangeln är rätvinkling och har förutom vinkeln 90° också vinklarna på 60° och 30°. Hur kan Jon-Erik konstruera en vinkel på 15° om han inte får använda några andra redskap än plasttriangeln och papper?

Diskussion

Det här problemet förutsätter att vi får använda penna (och triangelns raka delar kan användas som linjal). För att lösa problemet, prova att rita av plasttriangeln på flera olika sätt och sedan sammaföra bilderna med varandra.

Eftersom 15° är hälften av 30°, så kan det vara bra att få en symmetrisk bild, så den vinkeln vi vill ha dyker upp av sig själv.

Lösning

En möjlig lösning är att först rita av plasttriangeln , sedan vända upp och ner och till slut lägga ner den så att vinkeln med måttet 30° fortfarande utgör toppen. Rita av triangeln igen och dra sedan en linje mellan toppen och skärningspunkten av de motstående sidorna.

På grund av bildens symmetri kommer vinkeln att delas mitt itu. Linjen som delar en vinkel på mitten kallas förresten för bisektris.

Lösningen till problemet för de äldre vecka 38

Mattegåta

En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.

Om S⁺ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S^– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S⁺-S^– lika med?

Diskussion

När problem handlar om att jämföra areor, så är det ofta så att delar av de här areorna är lika, speciellt när delarna har konstiga former (jämför med problemet för de yngre vecka 35).

Börja med att rita den enklare varianten (då cirkelns mitt är i första kvadranten) och försök att ta bort så många lika stora delar från S⁺ och S^– som möjligt och jämför det som blir kvar.

Lösning (av Johan Björklund, något modifierad)

Proof by picture:

Jag tillför två hjälplinjer paralella med koordinataxlarna genom (2a,2b). De är spegelbilder av koordinataxlarna speglade genom linjer (igenom parallella med koordinataxlar) genom (a,b).

Det är lätt att se att flera av områdena har lika area (markerat med bokstäver). De kommer att ta ut varandra när vi beräknar S⁺-S^– (S⁺ är den gula plus den rosa arean, medan S^– är den gula plus den blå). Kvar blir den centrala rektangeln med area 4ab.

Tillägg (av Erik Svensson)

Detta var ifall mittpunkten låg i den första kvadranten. Om den istället ligger i den tredje kvadranten, då är fallet uppenbart det samma efter rotation med ett halvt varv, och ifall mittpunkten ligger i andra eller fjärde kvadranten, då speglar vi i y- respektive x-axeln och får samma fall fast med S+ och S- ombytt, så att den sökta arean byter tecken.

Vi finner emellertid att just 2a * 2b ändå uttrycker arean i samtliga dessa fall.

Lösningen till problemet för de äldre vecka 35

Mattegåta

Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.

Diskussion

Hur ska den här konstiga formuleringen tolkas?

Jo, att polygonerna har bara lodräta och vågräta sidor, så vinklarna överallt är 90 grader (eller 270). Och att alla figurera är kongruenta.

Vad betyder det att två figurer är kongruenta? Med det menas att man kan ta första figuren, flytta den på något sätt och precis täcka den andra figuren. Man får rotera och vända på den första figuren som man vill.

Faktum är att alla sådana här rörelser antingen är rotationer, speglingar, translationer eller kombinationer av de tre sakerna. Vi vet att rena translationer är förbjudna enligt uppgiften. Så det gäller att bestämma antalet sätt att rotera och spegla en figur så det alltid blir olika positionerade figurer. Sedan ska man hitta på ett exempel med det antalet också.

Lösning (av Erik Thörnblad)

Jag hävdar att åtta är det maximala antalet:
Bevis:
Rimligtvis har polygonerna hörn. Kolla på ett specifikt hörn. Kalla ena änden för A och andra änden för B. När man sedan roterar polygonen och bara tittar på just det hörnet, så framgår det att det finns totalt åtta olika sätt att vrida hörnet på, så att sidorna hela tiden är parallella med kvadratens sidor (som jag nu antagit är lodräta och vågräta).

Detta innebär att man som mest kan skapa åtta polygoner som uppfyller alla krav som ställts.