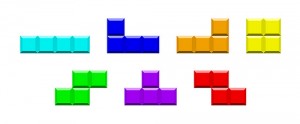
Varken figur a) eller figur b) går att bygga.
Låt oss anta att figurerna går att bygga. Färga rutorna i båda figurerna i ett schackrutigt mönster och se vad tetrisbrickorna läggs på för färger. Alla brickor förutom den T-formade kommer att täcka över precis två svarta och två vita rutor. Den T-formade tetrisbrickan kommer att täcka över tre vita och en svart eller tre svarta och en vit.
Räkna dock antalet svarta respektive vita rutor i de stora figurerna:
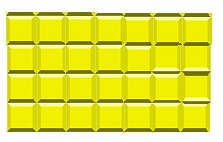
a) hälften svarta, hälften vita, det vill säga 14 svarta samt 14 vita.
b) om den stora diagonalen färgas svart, blir det 16 svarta samt 12 vita rutor.
Men antalet svarta rutor måste enligt tetrisbrickorna vara 2 * 6 + 3 eller 2 * 6 + 1, det vill säga 15 eller 13, vilket ger oss en motsägelse.


fcking omöjligt
Sjukt svår. Den här har vi inte klarat av.
Uppgiften påstår inte att det är möjligt. Om ni tror att någon figur är omöjlig, försök att bevisa det på något sätt.
Bevis är det när ni kan övertyga någon annan om att det faktiskt är omöjligt.
Här finns en diskussion om ett liknande problem, om någon är intresserad. http://math.stackexchange.com/questions/80246/the-mathematics-of-tetris
Uppgiften är enkel, bara man har hört talas om färgläggning, vilket jag för övrigt fick lära mig på Sonja Kovalevsky-dagarna. Färglägg som ett schackbräde och undersök hur många rutor av varje sort bitarna tar upp, så är det klart.
Finns det något annat angreppsätt än schackrutor?
Toomas: inte vad jag känner till, i alla fall inte på det här problemet.
Andra vanliga mönster man annars brukar använda är ränder (varannan rad vit, varannan svart), diagonala ränder av fler olika färger (schackmönster är ett specialfall av det), bredare ränder, större schackrutor (en ruta kan vara en 2×2-kvadrat).