Nyligen pratade jag med en kollega om ekvationer. Att så pass måna barn och ungdomar i Sverige har svårt att förstå hur ekvationer funkar.
En möjlig förklaring till detta är att det blir för stort hopp i abstrakt tänkande när ekvationer först introduceras. Många elever tycker inte om 
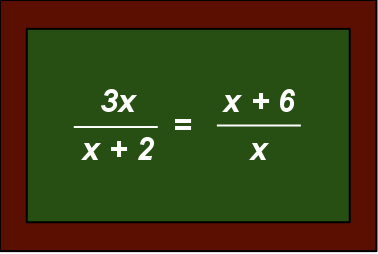
Egentligen är ju ekvationer ganska enkelt! (Som all matematik, när man väl fattar.) Ett sätt att få elever att inte bli rädda för det nya skrivsättet är att introducera x tidigare i grunskolan, föreslog min kollega.
Ni har säkert sett något liknande i matteboken på lågstadiet:
Eller ett streck eller till och med en glad gubbe istället för rutan.
Varför inte skriva
Barnen får skriva en siffra på platsen där
vilket antagligen gör de mindre rädda för variabler så småningom. (Naturligvis bör olika bokstäver användas, inte uteslutande
Det är en intressant idé, men jag ser omedelbart en nackdel för elever som senare börjar läsa på gymnasienivå och träffar på ekvationer och formler av typen
där
Är det inte egentligen ett missförstånd från början att ”är” ett specifikt tal? Om någon ber mig lösa ekvationen 12-7=x så är den ”egentliga” frågan hitta mängden av alla (troligen reella) tal sådana att ekvationen uppfylls. I exempelvis din bild av en ekvationen på tavlan så kan det ju mycket väl finnas flera lösningar, och det kan också finnas ekvationer utan lösningar. Det känns som en risk att man kan få för sig att en ekvation har en (och endast en) lösning. På samma sätt så borde man egentligen då man diskuterar funktioner göra skillnad på att definiera en funktion ( f(x):=2^x ) och använda ekvationer ( f(x)=2^x upppfylls för alla x).
Jag håller med om att man troligen skrämmer folk mer än nödvändigt genom att ”gömma” bokstäverna tills de blivit äldre. Jag tror man skulle kunna införa det på ett mer lekfullt sätt ganska tidigt genom att exempelvis först prata litegrann om siffror som symboler (man användersiffran 3 för att beteckna tre objekt eftersom siffran 3 har tre vinklar om man ritar den med streck osv för de andra siffrorna). Accepterar man att siffror är symboler så borde det inte vara så skrämmande att ha en uppgift i stil med att ”Anna tycker inte om att använda de vanliga siffrorna för vissa tal utan använder bokstäver istället, i hennes book så står det 12-x=7. Vilken siffra kallar Anna för x?”. Om man accepterar att de vanliga siffrorna egentligen också bara är symboler så kanske det är lättare att acceptera att bokstäver också får vara med.
Att hitta vinklar på siffror och se hur de korresponderar mot vad siffrorna representerar kanske skulle kunna vara en passande övning för din barngrupp?
Värt att nämnas är att de nya kursplanerna föreskriver att ekvationer skall läras ut redan från mellanstadiet, till skillnad från den gamla kursplanen, där det (på riktigt) introducerades på högstadiet.
Det där mer korrespondens mellan siffrornas form och betydelse, har du nån länk till det, Johan? Jag har hittills bara stött på att det är lite av en myt.
En annan aspekt av ekvationer man borde introducera tidigare är att det egentligen betyder jämvikt. Det finns förvisso uppgifter där man får se en balansvåg där några objekt är i jämvikt och så ska man få ut information om objekten (t.ex. två tegelstenar väger lika mycket som 6 flaskor vatten, vad är i jämvikt med en tegelsten?), men sådana uppgifter finns det ganska få av. Och de kopplas inte tydligt till algebraiska uppställningar heller, när man väl introducerar ekvationer.
Hmm, jag tror du har rätt i att det är lite mer av en myt tyvärr (även om inte det hindrar att man räknar vinklar iofs). Däremot så finns det en del korrespondenser mellan form/betydelse för låga tal, 1 är ett streck, 2 är två streck, 3 är tre streck (med ganska god vilja), sedan så blir det mer komplicerat tyvärr.
Det kanske ändå går att introducera genom att titta på lite olika siffersystem och hur man skriver saker (romerska, maya etc) så att det inte känns konstigt att något annat egentligen kan stå för en siffra. Mayaindianernas räknesätt är väldigt lätt att ”se” vad en siffra står för så det borde gå att göra några trevliga uppgifter om som även de yngre skulle kunna förstå medans kanske romerska siffror skulle passa bättre för de äldre.
Jag vet att det finns en någon urbefolkningsstam som använder kroppsdelar för att räkna (ordet för ett är samma som ordet för vänster lillfinger etc) vilket kanske också skulle kunna användas i någon form av lek (kommer inte ihåg vad stammen hette men jag tror jag läste om det i brian butterworths ”the mathematical brain”, mycket intressant bok av en neuropsykolog, den tar upp en del om hur hjärnans matematiska förmåga utvecklas med ålder också så den kanske vore speciellt intressant för dig som undervisar yngre barn).
Jämvikt är ett bra sätt att se det på (även om det kanske egentligen är en ekvivalensrelation snarare än en likhet). Det har ju också fördelen att man lätt kommer in på olikheter i termer av vilken sida som väger över.