Aktiviteten trassel
Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)
Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse
Tid: 45 minuter
Antalet deltagare: 4 + publik
Aktiviteten ”trassel” kommer från matematikern och pusselkonstruktören Johan Conway och har genomförts i Sverige på bland annat Sonja Kovalevsky-dagarna. Den passar att genomföra på en matematiklektion om bråkräkning/gruppteori eller som en extra matematikaktivitet.
Man börjar med att fyra elever ställer sig som hörnen på en kvadrat inför resten av klassen. Var och en av dem tar tag i var sin ände av ett rep så att repen hänger parallella med hur publiken sitter. Under experimentet får de aldrig släppa sin ände.
Så här ser det ut uppifrån (Positionerna närmast klassen är D och C):
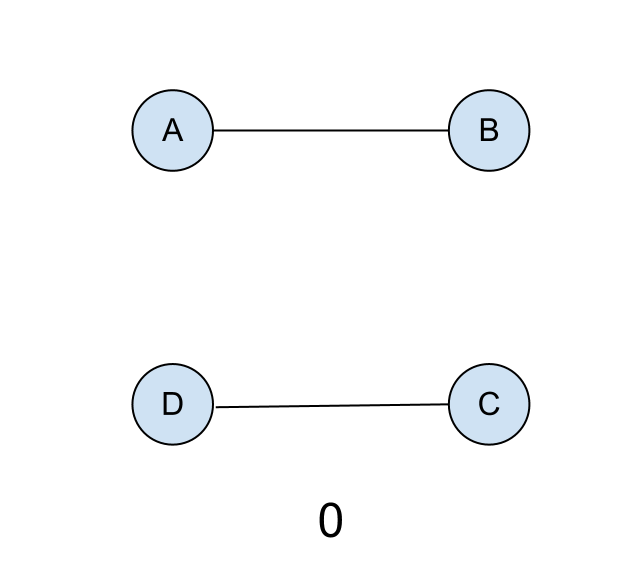
Nu kommer de fyra personerna utföra en slags dans och trassla till repen samtidigt. Varje trassel (tangle) repen bildar kommer att ha ett motsvarande tal. Från början, när repen är parallella mot varandra och mot klassen, motsvarar det talet 0.
Det första tillåtna danssteget är att vrida om repen runt varandra. Och inte på vilket sätt som helst, utan det måste göras av personerna som står på positionerna B och C. Dessa två personer byter plats med varandra och B är den som lyfter sin repände, som C går under för att komma till sin nya position.
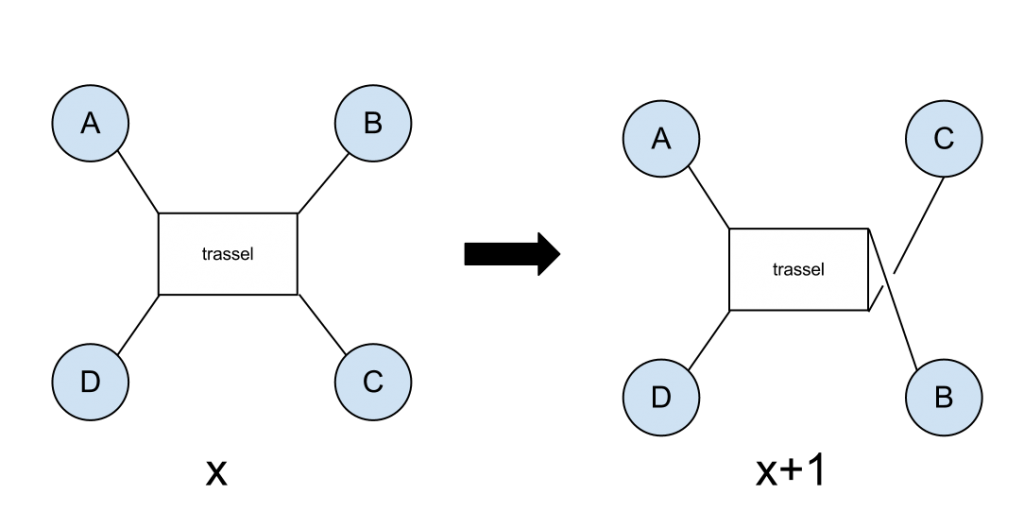
Att vrida om trasslet på det här sättet kommer att öka talet med 1. Så en omvridning ger ett trassel med värdet 1, medan en till omvridning ger talet 2 osv.
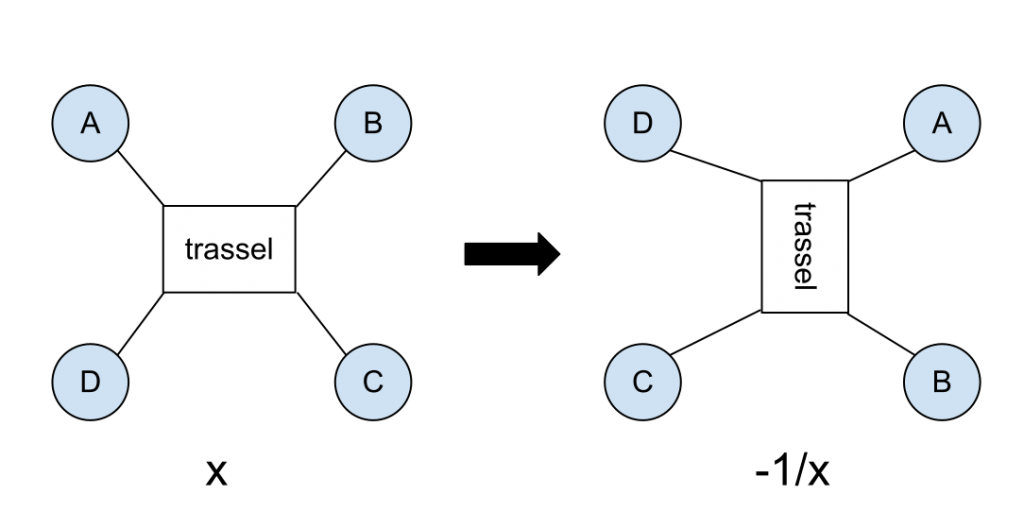
Det andra tillåtna danssteget är att rotera medurs. Person A går till position B, person B går till position C och så vidare.
Att rotera trasslet kommer också att förändra talet. Men hur? Om elevera har hållit på med funktioner och algebra tidigare kan man låta dem att lista ur svaret. Annars kan man helt enkelt säga att talet x omvandlas till talet -1/x vid en sådan rotation. Notera t.ex. att två rotationer i rad inte gör någon skillnad på trasslet, vilket är klart för trassel som består av några omvridningar:
n -> -1/n -> -(1/(-1/n)) = n
När alla har förstått reglerna kan man be eleverna att uföra några danssteg (börja med att först
vrida om), samtidigt som man räknar på talet som ska motsvara trasslet. Om man från början gör dansstegen: vrida om, vrida om, rotera, vrida om, vrida om, vrida om, rotera, vrida om så kommer man till talet:
0 -> 1 -> 2 -> -1/2 -> 1/2 -> 3/2 -> 5/2 -> -2/5 -> 3/5
Hur ska man lösa upp detta trassel om man bara tillåts att göra dansstegen ovan? Publiken får lösa denna uppgift genom att försöka räkna ut hur man ska göra med bråket 3/5 för att det ska bli 0, om man bara tillåts addera 1 och ta den negativa inversen. Man kan ju inte göra dansstegen ”baklänges”, eftersom steget ”att vrida runt åt andra hållet” inte finns.
När någon har kommit på dansstegsföljden kan man testa dansen och se att knuten verkligen löses upp.
Det här kan man göra med andra tal. Ju svårare trasslet är, desto roligare blir det att se det lösas upp. När repen är tilltrasslade, kan man knyta några plastpåsar runt dem, så att trasslet inte syns och sedan utföra dansstegen som eventuellt ska lösa upp trasslet. När talet på tavlan är 0 kan man knyta upp påsarna och se att allt blir som i början, bara man drar i repen!
Fler frågor att diskutera på avancerad nivå:
– Vad händer om man roterar först? Vad är talet -1/0 och vad har det för egenskaper? Ska trasslet -1/0 förändras om man vrider om det?
– Hitta inversen till att vrida om. Det vill säga, om man startar från ett trassel och sedan vrider om en gång, vad för danssteg skall man göra för att komma tillbaka till starttrasslet?
Fler frågor för att grupper:
– Om man börjar från 0, hur kommer man till ett specifikt trassel, t.ex. -3?
– Hut kommer man snabbast ner till 0 från ett specifikt trassel? Här kan eleverna tävla om vem som kan hitta på kortaste dansstegsekvensen när trasslet är ett relativt avancerat bråktal.
Mer om aktiviteten kan du läsa i Conways text (tangles börjar på sida 10) conway.pdf, samt Tom Davis text med utförlig diskussion och beskrivning av aktiviteten. tangle.pdf.
Tack till Johan Björklund för tipset!
