genikampen – Mattebloggen

Matematik i Genikampen – fjärde och femte avsnittet

Första, andra och tredje avsnittet av Genikampen innehöll en hel del matte, medan avsnitt fyra och fem var mycker mer fysikinriktade. Jag har inte så bra förståelse för fysik, så jag ska försöka framlägga hur jag försökte göra mitt bästa genom att tänka logiskt och matematiskt i tävlingarna. Samt hur man skulle kunna gjort för att prestera ännu bättre!

Avsnitt 4: Robottävlingen

Tävlingen handlade om att sätta sig in i ett drag-and-drop programmeringsspråk för att skriva program som fick en Lego-robot att utföra uppdrag. Man kunde bygga ut roboten med några Lego-bitar för att underlätta uppdragsutförandet.

Det fanns många saker man kunde göra på banan, men lite tid. Det mest tricksiga var att programmet är kopplat till en verklig fysisk händelse, till skillnad från många ”vanliga” datorprogram. Till exempel innebär det att svänging på 90 grader i programmet inte innebar svängning på 90 grader i verkligheten, utan lite mer om roboten precis hade varit i rörelse. Jag antar att det beror på att den har lite rörelseenergi/intertia/eller vad det heter. Vi fick exempel på hur dessa värden kunde motsvara de verkliga, men inte riktigt någon formel, så det handlade om att prova sig fram helt enkelt, som i många andra tävlingar. Tyvärr fick man bara två försök på själva banan.

Om det inte var trivialt att anpassa speglar från avsnitt 2, där vinklarna faktiskt var mer eller mindre exakta, så var det otroligt mycket svårare här; oexaktheterna ställde till det.

Därför lyckades båda lagen bäst med det enklaste programmet, som körde roboten fram och sedan tillbaka. Jag tror att tävlingen hade blivit roligare, ifall man inte hade fått dubbla poäng för att köra tillbaka roboten. Då skulle man ha vågat sig på någon svårare bana tror jag, och det laget som hade kommit längst i sina eskapader skulle ha vunnit.

Men alla snitsiga planer och programmeringskunskaper hjälper inte, när man inte ens kan stoppa in USB:n på rätt sätt för att det nya programmet ska laddas över till roboten :)

Hur som helst hade det gula laget kommit längre med sitt projekt, så det var en välförtjänt vinst. Men det hade varit spännande att se hur det skulle ha gått till ifall vi ”genier” hade fått öva på Lego-programmering innan. Annars var det lite som att vi skulle ha slängts i vatten i våtdräkter och behövt dyka utan att ha provat på det först!

Avsnitt 4: Bron

I den här tävlingen gällde det att vara stabil! De vinnande taktikerna gick ut dels på att två personer på bron samtidigt stabiliserar varandra och dels på att två plankor under en person stabiliserar personen bättre.

Så hur ska man såga i plankorna? För rakar rep är svaret självklart: såga skårorna på samma avstånd som repen är! För korsade rep är det lite svårare, det beror på var man fick ha plankan! Jag tror att Johan vill ha en kort planka en tredje del in (dvs förhållandet mellan avståndet bryggkant-planka skulle vara dubbelt så stort som planka-kryss). Då skulle avståndet mellan skårorna på grund av likformighet vara en tredje del av avståndet mellan repen. Vi hade ingen linjal eller måttband, men vi visste dessa avstånd. Därför kunde vi på ett ungefär räkna ut (med halveringsmetoden) var man skulle göra skårorna. Vinkeln gissade vi på :) Och det funkade!

Avsnitt 4: Pusselduellen

Svårt att skriva om en tävling som man inte fick testa på! Den första pyramidpusslet hade jag sett förut, den är icke-trivial! Ett sätt att lösa det på är att få till en bit att ligga med ”rätt” vinkel, dvs en vinkel som känns vettig med tanke på slutresultatet. Då blir det tämligen rätt att fylla i slutresultatet, med tanke på att pusslet dessutom är spegelsymmetriskt.

Angående andra pusslet säger Theres att det är fyra likadana bitar. Det är lite svårt att se på videon, men jag tycker att de bara nästan är likadana. Det underlättar enormt om bitar är exakt likadana: Då vet man att en sådan bit måste innhålla översta kulan t.ex. och så börjar man testa sätt som den biten kan ligga på. Man ser också att Theresa behövde bygga ihop bitarna ”alla samtidigt”, det gick inte att sätta in dem en i taget. Detta är något av det svåraste att komma i pussel. Lättare pussel, liksom matteproblem, löses ett steg i taget (och man förstår vilka steg det är som ska tas). I de svårare måste man däremot komma på en följd av steg som löser det, vilket i mitt tycke är exponentiellt mycket svårare!

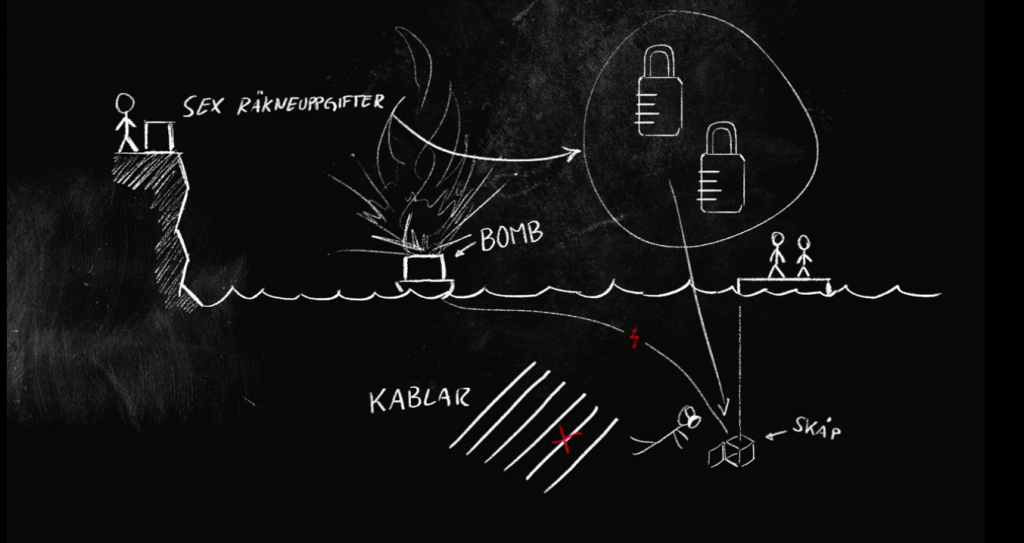
Avsnitt 5: Flygplansbomben

I flygplanstävlingen skulle vi räkna ut tiden att släppa en kalkbomb på för att den skulle åka ett visst avstånde. Så som Axel säger är det en vanlig uppgift från fysikböcker. Vad händer då när ”genier” ska räkna på det på riktigt?

Msn sätter upp en modell, som tar hänsyn till hastighet och acceleration och sätter in de kända värden. Varför blir det så fel? Dels är luftmotståndet tydligen svår att beräkna exakt, men dels tror jag det skedde missförstånd. Vi fick planets hastighet relativt marken trodde vi, men det var nog relativt luften. Det borde vi kanske ha insett när det blev så mycket fel, men jag hade ingen intuition för fysik, så tyckte inte det var så värst dåligt resultat att hamna 65 m bakom. Hade jag gjort det själv skulle det inte gått lika bra tror jag! Jag skulle iofs använt en enklare modell.

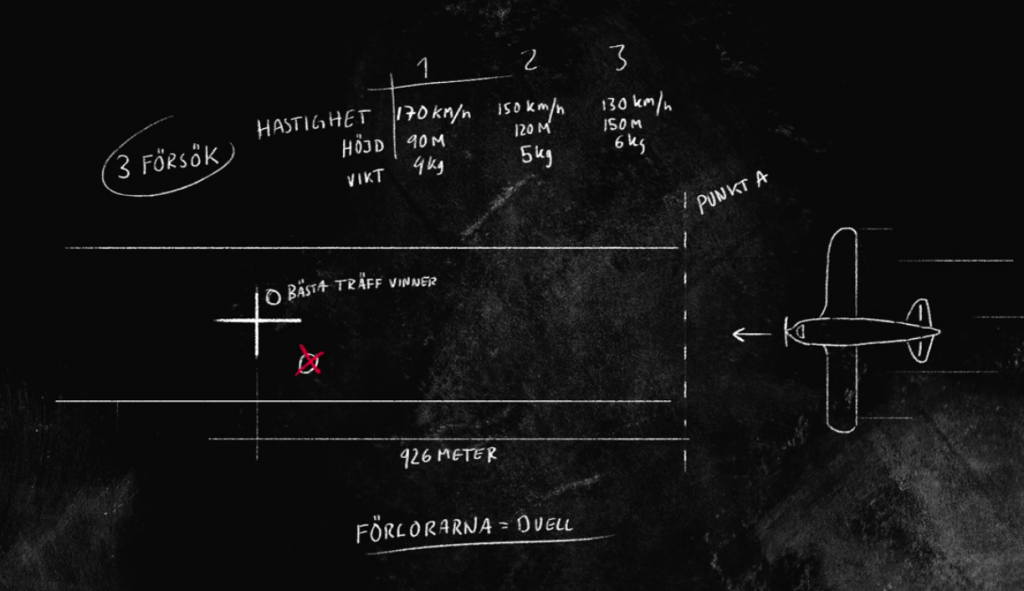
Poängen är att om modellen inte fungerar perfekt handlar inte om att hitta en bättre modell snabbt, utan att modifiera svaren utefter hur fel de var. Detta är precis vad gula laget gjorde och de vann på det! Fredrik lade fram ett hypotetiskt värde genom att ställa upp ett linjärt samband ”x sekunder = y meter”. Det var lite tur att det fungerade, men det var ju helt rätt tänkt tänkt. Det berodde på att hastigheterna på planet ökade linjärt (170 km/h – 150 km/h – 130 km/h) och samma sak gällde höjden (och vikten). Allt som allt tror jag det borde blir ett linjärt samband för tid-avstånd också, i alla fall för små förändringar. Kul att det fungerade!

Avsnitt 5: Tryckluftkanoner

Jag kunde i stort sett ingenting om tryck när jag gick in i tävlingen, men efteråt berättade Axel om hur man modellerar skottkurvan utefter tryck och storlek och sådär. Vi räknade ut lite vinklar efteråt i lugn och ro, det var roligt!

När det gällde att komma på vinklar snabbt och bygga finns det ingen tid för räkning tyvärr. Det handlar mer om praktiska erfarenheter och tänk (hur fixar man läckande kanon). Där är en matematisk hjärna till ingen nytta!

Övningen med vattenmelonerna kunde man däremot tänka lite på. Fredrik har återigen rätt i att om uppgiften ska lösas med empiri så är det bara en parameter i taget som man tjänar på att ändra på.

Hur kunde man räkna ut den ungefärliga vinkeln? Jag gjorde det genom att rita en triangel på tavlan som var likformig med vår skjutbana (vi antog att kanonen skulle skjuta rakt uppåt om vi hade maximalt lufttryck) och sedan lägga på likadana vinklar (egentligen fördubbla dem) tills det skulle bli 90. Sedan kan man gå baklänges och räkna ut den ursprungliga vinkeln. Då fick vi 10.

I verkligheten beter sig inte saker perfekt, alltså inte som i modellen. Kanonen skjuter inte rakt uppåt och inte rakt framåt heller för den delen (som man ser blev det fler skott till vänster om målet än till höger). Återigen löser man uppgiften bäst genom att titta på det som faktiskt hände (här var referensskottet jätteviktigt att tänka på) och sedan anpassa sina värden därefter. Modeller är bra när man inte har någon aning, men har man något att utgå ifrån så borde man göra just det. Ännu än vinst för empiri!

Avsnitt 5: Stavningsduell

Inte särskilt mycket matte här, men bra att hålla reda på en regel för att skilja på enkelbokstav och dubbelbokstav. Överensstämma = överens + stämma (haha, lite matte blev det ändå), så det ska vara två ”s”. Kom dock ihåg att det kan aldrig bli tre ”s” (eller någon annan bokstav för den delen), utan de förkortast alltid till två i svenskan. Exempel: tuggummi = tugg + gummi.

Matematik i Genikampen – tredje avsnittet

Tredje avsnittet av Genikampen innehöll mycket matte! Så mycket att det inte hanns med att skriva om det innan avsnitt fyra kom ut. Avsnitt fyra och fem kommer jag däremot att slå ihop till ett inlägg.

Avsnitt tre innehöll tre tävlingar: allmänbildningspyramiden, bombdesarmering och pussel i duellen.

Pyramiden

I pyramidtävlingen skulle vi välja ett av fyra svarsalternativ på varje fråga, ställa in lådorna med de sidorna framåt och sedan klättra upp på pyramiden för att få en kontroll. Programledaren Micke skulle då säga hur många rätt vi hade (men förstås inte vilka som var rätt) och då kunde vi ändra lådorna till nästa kontroll. Det gällde att få alla rätt, men hur ska man göra om man inte kan svaret på frågorna?

Hade man fått veta vilka frågor man hade fått fel på, så skulle det inte ta mer än fyra testomgångar för att lyckas få alla rätt — då tar man ju bara hela tiden nästa alternativ på de som är fel. Eftersom man bara får veta antalet, så gäller det att chansa lite vilka frågor man hade fått fel på.

Mer om detta senare, men i verkliga förloppet hade vi verkligen tur med att snabbt få noll rätt.

Som sagt i programmet ger detta oss nu 3^10 = 59049 möjliga kombinationer för de rätta svaren som ska testat istället för 4^10 = 1048576, nästan 18 gånger färre det vill säga! I termer av utvunnen information är det till och med lite sämre att få fem rätt, då man inte vet vilka fem det är och resterande fem kan varieras på tre sätt, så antalet kombos som fortfarande funkar är:

${10 \choose 5}\cdot 3^5 = 61236$

Noll rätt är dessutom riktigt bra att få tidigt, då framtida manipulationer av lådor kan bara göras på tre sätt istället för fyra (om man nu kommer ihåg de felaktiga alternativen, men vi utgår från perfekt minne här förstås).

Nu är det intressant att avgöra vilken taktik som snabbast ger en alla rätt om man bara chansar (och inte använder faktakunskaper man tror man besitter, hade vi kunnat någon fråga så hade vi nog inte fått noll rätt :)).

För enkelhets skull jämför vi två taktiker: att chansa på en låda i taget eller att chansa på två lådor i taget (och sedan förändra dem en och en för att få båda rätt). Att vända på lådorna tar ungefär lika lång tid som att att vänta på svar från programledaren, så det är det totala antalet ”försök” som avgör tiden det tar att testa sig fram.

Om man vänder på en låda i taget (och har tre alternativ som kan vara rätt), så är det en på tre att man gissar rätt och två på tre att man gissar fel. I det andra fallet behöver man max gissa en gång till, sedan kan man gå vidare till nästa låda, eftersom man vet vilket alternativ som är rätt. Det allra sista kontrollen kan vi alltså bortse från (försumbart). Således, väntevärdet på antalet försök är:

$\frac{1}{3}\cdot 1 + \frac{2}{3}\cdot 2 = \frac{5}{3}$

Gör man detta för två lådor, blir väntevärdet då lite mer än 3.

Om vi vänder två lådor i taget kan vi få tre alternativ: antalet rätt ökar med 2, med 1 eller med 0. Om två lådor är rätt behövdes det då ett försök, om en låda är rätt, så behöver man först vända en av dem för att bestämma vilken låda som var rätt (om man vänder på den som var fel kommer antalet rätt öka med 0 eller 1 (det senare fallet händer med mycket liten sannolikhet), annars minska), sedan kommer man antingen behöva testa noll/ett alternativ till (om man vände på den lådan som var fel) eller ett/två alternativ (om man saboterade den lådan som var fel från början). Om man har däremot 0 rätt från början så vänder man på båda lådorna igen och sedan behöver vända en eller två gånger till för att få båda rätt. Totalt blir väntevärdet ungefär följande:

$\frac{1}{9}\cdot 1 + \frac{4}{9}\cdot (\frac{1}{2}\cdot (\frac{1}{3}\cdot 1 + \frac{2}{3}\cdot 2) + \frac{1}{2}\cdot (\frac{1}{3}\cdot 2 + \frac{2}{3}\cdot 3)) + \frac{4}{9}\cdot (\frac{1}{4}\cdot 2 + \frac{2}{4}\cdot 3 + \frac{1}{4}\cdot 2)$

vilket också är lite mer än 3!

Därför spelar det inte så stor roll om man testar en låda i taget eller två (och sedan fixar till lådorna en och en). I längden får man göra lika många försök i alla fall.

Sedan är ju frågan om man ska gå efter genomsnittsfallet (3 försök på båda strategierna), på värsta fallet (att man har maximalt otur) eller på det bästa fallet (att man har maximalt tur).

Första strategin (vända en låda i taget) har följande antal försök (innan man vet de rätta svaren) på vart och ett av fallen:

Värsta fallet: 5
Genomsnittsfallet: 3
Bästa fallet: 2

Andra strategin har följande:

Värsta fallet: 4
Genomsnittsfallet: 3
Bästa fallet: 1

Detta visar på att om man vill köra ”safe” så ska man satsa på andra strategin, då man behöver försöka färre gånger om man har otur. Men ointuitivt nog ska man också köra på den om man vill köra ”djärvt” och vill kunna klara pyramiden på färsta möjliga antalet försök. Den första strategin är helt enkelt för ”långsam”. Detta förutsätter att man har bra minne, men i övrigt tror jag båda lagen körde på den här strategin, vilket visar på en bra intuition för matematik och sannolikheter hos deltagarna.

Bombdesarmeringen

I andra tävlingen skulle lagen komma på ett kommunikationssystem för att kunna överföra siffrorna 0-9 och bokstäverna A-J utan ljud på ett långt avstånd till sina lagkamrater. För att inte hålla för mycket i huvudet kom båda lagen på ett system för antingen siffrorna eller bokstäverna och endast den typen skickades (gult lag skickade siffror, blått — bokstäver). Sedan översatte mottagarna på flotten: A=0, B=1, C=2 och så vidare. Detta system förutsätter att mottagarna inte till exempel råkar tänka att A=1. Effekten +/-1 är annars är ett vanligt fel vuxna brukar göra, till exempel när de programmerar eller beräknar antalet dagar i ett visst tidsintervall.

Systemet med siffror tyckte vi hade en fördel, eftersom uppgifterna gick ut på att få fram siffror, både i del 1 och del 2. Det hade varit lite extraarbete och osäkerheterna kommer in när man först ska översätta siffran till en bokstav, skicka bokstaven och sedan ska bokstaven översättas tillbaka till siffran i del 1. Men det verkade blå laget klara bra, det var inte det som var svårast, utan att lösa uppgifterna var det. Sedan är det ju en fördel i andra delen, att skicka bokstäverna direkt. I vilket fall blir det samma antal översättningarna för båda strategierna i andra delen.

När jag ändå pratar om osäkerhetsfaktorer, så är det just på grund av dem som det hade varit bra att skicka all information på en gång i andra omgången. Dykaren får veta fem bokstäver vars motsvarande kablar hen ska klippa. OM man räknat fel så finns det stor sannolikhet att kabeln med bokstaven inte ens finns. (OM man till exempel får två likadana siffror som svar så vet man redan på berget att man har gjort fel. Det vet man inte om man skickar en siffra i taget.) Då kan dykaren låta bli att klippa något och säga att en viss bokstav inte finns, vilket mottaggarna får försöka kommunicera tillbaka till räknarna.

Lag gult hann inte dock skicka ut någon information i del 2, utav vi fokuserade på att kontrollräkna istället då vi inte fick några likadana siffror.

Vad gäller del 1 så var det bra att skicka ett lås i taget, då man kan kolla just ett lås i taget (och inte en siffra i taget), om det är rätt, och kostnaden för fel är mycket mindre.

Här hittar du lösningar till alla uppgifter. Som jag nämner i det inlägget så kunde man löst uppgifterna på ett ännu smartare sätt, då man visste att svaret skulle bli en siffra. En smart lösning som min kompis Johan B tipsade mig till uppgiften

((√256 x 20 − 25^2 + 15^2 + 3^4) x 10) / 5 = ?

är följande:

Vi vill veta vilken siffra som resultatet är, därför räcker det att betrakta uppgiften ”modulo 10”, det vill säga studera slutsiffram i varje steg. Till exempel ser vi att vi har uttrycket (√256 x 20 − 252 + 152 + 34) x 2, därför kommer siffran att bli jämn. Och därför räcker att kolla vad uttrycket innan x 2 kommer att vara modulo 5. √256 x 20 slutar på 0 oavsett vad √256 är, därför kan vi strunta i att räkna ut det. − 25^2 + 15^2 är båda delbara med 5 och därför inte kommer bidra till sista siffran när man multiplicerar med 2 i slutet. 3^4 är det enda viktiga och vi kan räkna ut att det slutar på 1. Därför blir slutsiffran 1×2=2.

På liknande sätt kunde man ha gjort med kabel 3-uppgiften (försök själv!)

(15 – 7)(1500 – 25) – 2200 x 3 – 8^4 – 2^10 – 79 = ?

Pusselduellen

Det var svårt att se pusslen under programinspelningen, så vi roade oss med att räkna antalet kombinationer som varje pussel kunde vara i. Sedan gäller det förstås att hitta en bra sökväg mellan alternativen för att lösa pusslen snabbt.

Första pusslet består av sex bitar. Det var kanske givet vilken bit som skulle vara längst ner (om det inte var givet kunde man ta en godtycklig bit), så de resterande bitarna kan du placera på 5!*8^5 = 3932160 olika sätt (när du väl väljer en bit och en plats kan du vrida biten på 8 olika sätt vid den platsen, givetvis kommer de flesta sätt att direkt inte passa). Det är såklart inte rimligt att testa alla de sätten då en människa kan direkt se vad som passar och vad som inte passar. Ganska enkel brute force löser uppgiften i det här fallet.

Andra pusslet bestod av 18 bitar! Om man nu bara testar att lägga ner dem som en apa (utan att bry sig om hålen), så kan man göra det på 18!*4^18 sätt (varje pinne kan placeras på 4 sätt, em kombination av bak-och-fram eller inte och upp-och-ner eller inte), och det är för stort för att få plats i Google miniräknare-fönstret (storleksordningen 10^26)! Sedan kan man ha vissa symmetrier på hela konstruktioner, men det är bara en liten konstant som man delar med.
Man kan inte minska sökvägen jättemycket här heller, utan det finns väldigt många kombinationer ändå. Man får utgå från olika bitsorter och testa att starta på olika sätt. Inte konstigt att det tog lång tid…

Tredje pusslet är lättare än den andra, då det innehåller färre bitar. Här är tricket att börja med den största biten, den med mest volym och testa alla möjligheter för hur den kan sitta i den stora (än imaginära) kuben. Sedan ska den näst största biten in och så vidare. På så sätt kapar man sökträdet som bäst i början. Här är det svårt att uppskatta antalet kombinationer som behöver ”testas”, då pusslet har en mycket oregelbunden struktur.

Matematik i Genikampen – kluringar från tredje avsnittet

Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de alla.

Kodlås 1 bestod av tre uppgifter, där varje uppgift gav en siffra. Den tresiffriga koden skulle låsa upp det första låset under vatten.
Kodlås 2 gav på samma sätt ett tresiffrigt kod till andra låset.
Kablar 5 uppgifter gav 5 siffersvar, där 0 stod för A, 1 stod för B och så vidare till 9 som stod för J. Bokstäverna var kopplade till kablar som var safe att klippa av.

Kodlås 1

sifferkod 1

Sofie och Maria är syskon. För deras åldrar gäller följande samband: Summan är lika stor som produkten. Hur gamla är Sofia och Maria?

Addera talen.

Det här var enda uppgiften vi först gjorde fel på!

Den går ut på lista ut åldrarna S och M sådana att S+M = S·M.
Ekvationen S·M − S − M = 0 beskriver en hyperbel, som har oändligt många punkter. Men eftersom vi frågas efter heltalslösningar (och det bara ska vara en lösning som funkar), så funkar det bra att gissa.

Vi gissade på 0+0 = 0·0, men 2+2 = 2·2 funkar också. Det senare betraktas troligare som ålder (kanske säger man aldrig att någon är 0 år gammal), så svaret var 4 (och inte 0 som vi först trodde).

Första kodlåssiffran är 4.

sifferkod 2

En tjuv stal en säck med guldmynt i ett slott. För att komma ut ur slottet måste han passera tre vakter. Den första mutade han genom att ge vakten hälften av guldmynten. Vakten gav dock tillbaka 100 guldmynt av ren medkänsla. Den andra vakten fick hälften av tjuvens pengar men gav sedan tillbaka 50 guldmynt. Den tredje vakten fick hälften av pengarna men gav sedan tillbaka 25 guldmynt. Tjuven hade då 100 guldmynt kvar. Hur många mynt hade han från början?

Dividera svaret med 40.

Här är det lättast att gå baklänges. Tjuven hade 100 guldmynt i slutet.

Nu kollar vi hur mycket han hade innan varje händelse:
Innan tredje vakten gav honom 25 mynt hade han alltså 75 mynt (100-25).
Innan tredje vakten fick hälften av pengarna hade tjuven 150 mynt (75*2).
Innan andra vakten gav honom 50 mynt hade han 100 mynt (150-50).
Innan andra vakten gick hälften av pengarna hade han 200 mynt (100*2).
Innan första vakten gav honom 100 mynt hade han 100 mynt (200-100).
Innan första vakten fick hälften av pengarna hade han 200 mynt (100*2).

200/40 = 5.

Andra kodlåssiffran är 5.

sifferkod 3

Ett tåg består av ett lok och fem vagnar (A, B, C, D och E). På hur många sätt kan vagnarna ordnas så att vagn A kommer närmare loket än vagn B kommer?

Dividera svaret med antalet konsonanter i det svenska alfabetet.

Det går att ställa vagnarna på rad på 5! sätt. 5! står för uttrycket 5*4*3*2*1 = 120.
Detta beror på att en av de fem vagnarna kan ställas längst fram, en av de fyra kvarstående kan ställas på andra plats, en av de tre kvarstående på tredje plats, en av de två som är kvar kan ställas näst sist och ett alternativ har vi kvar för den vagnen som ska stå sist.

Exakt hälften av de ordningarna är sådana att A kommer närmare loket än B (och exakt hälften är tvärtom). Det beror på att alla ordningar kan paras ihop: varje ordning är i par med nästan samma ordning, fast där A och B har bytt plats. Till exempel är CADEB i par med CBDEA. Därför ska vi dela svaret med 2.

(Det här är för övrigt i stort sett samma uppgift som 2(a) här: LÄNK http://mattebloggen.com/wp-content/uploads/2014/09/Lektion2Permutationer.pdf)

120 / 2 = 60.

I det svenska alfabetet finns det 20 konsonanter (29 bokstäver totalt, varav 9 är vokaler).

60 / 20 = 3.

Tredje kodlåssiffran är 3.

Kodlås 2

sifferkod 1

Sofie satt på balkongen och gjorde sin matteläxa. Hon hade just skrivit svaret på en uppgift, när en duva kom flygande och lämnade sitt ”visitkort”, så att sista siffran (= entals siffran) i svaret inte syntes. Skillnaden mellan det ursprungliga svaret och det svar som nu syntes var 276. Vilket var det ursprungliga svaret?

Addera svarets siffror.

Om det ursprungliga slutsiffra var A, så kan talet skrivas som 10*X + A (oavsett hur många siffror talet har kan de skrivas som ett visst antal tiotal plus en slutsiffra).

När duvan har varit framme och busat hade Sofie talet X framme (antalet tiotal i det ursprungliga talet).
Det betyder att 10*X + A – X = 276
Det vill säga 9*X + A = 276.

Talet 276 är inte med i nians tabell, utan ger rest 6 när man dividerar med 9. Det betyder att A måste ha varit 6 och X i sin tur måste ha varit 30 (=270/9).

Så talet som stod där från början var 306 (=10*30+6). Detta är det enda svaret.

3+0+6 = 9

Första kodlåssiffran är 9.

sifferkod 2

Tre positiva heltal (naturliga tal) är så beskaffade, att om vart och ett multipliceras med de två övrigas summa, får man produkterna 120, 133 och 169. Bestäm talen.

Addera dessa tre tal och subtrahera det med det tal som kommer efter 13 i Fibonaccis talföljd.

Vi har tre tal som vi kan beteckna med a, b och c. Då vet vi att:

a*(b+c) = 120
b*(a+c) = 133
c*(a+b) = 169

Sen ska man bestämma talen står det, men det struntade vi i! Man skulle nämligen addera dessa tre tal senare, så vi fokuserade på att bestämma a+b+c (så man behöver inte bestämma vart och ett av talen).

c*(a+b) = 169. Eftersom 13*13 = 169 och 13 är ett primtal, går det bara skriva 169 som en produkt av tåv positiva heltal på två sätt:

169 = 13*13
169 = 1*169.

I det första fallet får vi att a+b+c = 13+13 = 26
I det andra fallet får vi att a+b+c = 1+169 = 170

Resan nu inser man att det är det första som är rätt (eftersom vi ska subtrahera 21 och få en siffra, men vi bevisar det korrekta svaret ändå utan att använda det).

133 = 7*19 och 7 och 19 är primtal, därav a+b+c är antingen 7+19=26 eller 1+133=134, så det måste vara 26!

(Detta stämmer även med faktoriseringen av 120 = 20*6 till exempel. Nu kan vi bestämma a, b och c för sig men det är för mycket jobb).

Fibonaccis talföljd är 1,1,2,3,5,8,13,21,34 och så vidare. Varje tal från och med det tredje är lika med summan av de två talen innan. Läs coola grejer om Fibonaccitalen

26 – 21 = 5

Andra kodlåssiffran är 5.

sifferkod 3

((√256 x 20 − 25² + 15² + 3⁴) x 10) / 5 =

Det här är bara en vanlig uträkning. Men man kan ändå räkna ut det lite smart:
Då 256 är 2 upphöjt till 8, så är roten ur det 2 upphöjt till 4, det vill säga 16.
Multiplicerar man den stora parentesen med 10 och sedan dividerar med 5, så är det samma sak som att multiplicera parentesen med 2.

Sedan räknar man ut potenserna.

Då får man följande uttryck och du kan följa lite hur man kan tänka för att räkna snabbare:
(16*20 – 625 + 225 + 81)*2 =
(320 + 225 + 81 – 625)*2 =
(320 + 306 – 625)*2 =
(26 – 25)*2 =
1*2 = 2

Tredje kodlåssiffran är 2.

Kablar

Kabel 1

(6y-7)/4 + (3y-5)/7 = (5y+78)/28

Vad är y?

Detta är en vanlig ekvation, dessutom ser man att 28 är en minsta gemensam multipeln till 4 och 7, så det lättaste är att få bråken till gemensam nämnare:

7*(6y-7)/28 + 4*(3y-5)/28 = (5y+78)/28

Nu kan vi glömma bort 28:

7*(6y-7) + 4*(3y-5) = (5y+78)

Multiplicerar in talen:

42y – 49 + 12y – 20 = 5y + 78

Förenklar:

42y + 12y – 5y = 78 + 49 + 20

49y = 147
7y = 21
y = 3

Första kabeln ska ha bokstaven (3=)D.

Kabel 2

I herrtruppen till VM i cykel hade lagledare Hjulström tagit ut cyklister från enbart två klubbar – lika många från varje klubb. När det var dags för lagtempo, visade ett testlopp att alla åkarna i stort sett var jämngoda.
Hjulström beslöt därför att ta med två cyklister från vardera klubb i lagtempolaget. Ändå gav detta inte mindre än 36 tänkbara lagsammansättningar! Hur många cyklister bestod truppen av?

Den här uppgiften var inte det lättaste att tolka, så vi försökte tolka på ett sätt som skulle ge ett ensiffrigt svar.

Vi vet att det finns n cyklister i var och en av de två klubbarna. Om man ska räkna hur många sätt det finns att välja två stycken ur en klubb får man det från uttrycket n*(n-1)/2 (n sätt att välja den första, n-1 sätt att välja den andra, dela med två för att ordningen på de inte spelar roll, precis samma idé som i vagnuppgiften).

För att få antalet sätt att sätta ihop laget måste man multiplicera sätten att välja två från första klubben och två från andra klubben, vilket ska ge 36. Då n är densamma för båda klubbarna, innebär det att det ska finnas 6 sätt att välja två pers från en av klubbarna (för att 6*6=36).

Nu får vi uppställningen n*(n-1)/2 = 6, vilket betyder att n*(n-1)=12, så n måste vara lika med 4.

Så då är frågan om vi ska svara 8 eller 4. Troligen 8 eftersom det verkar som att man räknar in båda klubbarna i truppen.

Andra kabeln ska ha bokstaven (8=)I

Kabel 3

(15 – 7)(1500 – 25) – 2200 x 3 – 8⁴ – 2¹⁰ – 79 =

En vanlig uträkning till! Tur att man kan sina tvåpotenser:
2¹⁰ = 1024
8⁴ = (2³)⁴ = 2¹² = 4096

(15 – 7)(1500 – 25) – 2200 x 3 – 8⁴ – 2¹⁰ – 79 =
8*1475 – 6600 – 4096 – 1024 – 79

Egentligen kan man bryta ut 8:an på tre ställen för att slippa räkna en stor multiplikation:

8*1475 – 8*825 – 8*512 – 8*128 – 79 =
= 8*(1475 – 825 – 512 – 128) – 79 =
= 8*(650 – 512 – 128) – 79 =
= 8*(138 – 128) – 79 =
= 8*10 – 79 =
= 80 – 79 =
= 1

Tredje kabeln ska ha bokstaven (1=)B

Kabel 4

Lille Micke sålde två fotbollskort för 21 kronor.
På det ena kortet tjänade han 10 % och på det andra kortet förlorade han 10 %.
Allt som allt tjänade han 5 %. Hur mycket hade varje fotbollskort kostat i inköp?

Svar: Addera dessa två tal och dividera summan med
den fjärde decimalen i pi.

Ett av de (till synes) svårare problemen! Lätt att virra ihop sig med procent. Men precis som i kodlåsproblemet med primtal behöver man inte lösa hela uppgiften. Vi ska ju använda summan av ursprungspriserna sedan, därför behöver vi egentligen inte ta reda på vart och ett av priserna, utan på vad det var tillsammans.

Om korten hade kostat A och B från början kan vi skriva villkoren som

21 = 1,1*A + 0,9*B = 1,05*(A + B).

Men om det är A+B vi är ute efter är uppgiftens andra rad helt onödig! Vi har:

21 = 1,05*(A + B)
A + B = 21/1,05 = 2100/105 = 300/15 = 100/5 = 20.

Och tur att man kan lite pidecimaler! 3,14159… Så svaret ska divideras med 5. 20/5 = 4.

Fjärde kabeln ska ha bokstaven (4=)E

Kabel 5

Då ett visst fyrsiffrigt tal multipliceras med fyra, får man ett nytt fyrsiffrigt
tal, där sifferföljden är omvänd jämfört med det första talet,
dvs. 4*ABCD = DCBA
Vilket är det ursprungliga talet?

Subtrahera svaret med 2004 och dividera den summan
med det tionde primtalet.

Här berättar jag en stor del av lösningen i tv. Men nu har jag chansen att kortfatta lösningen.

A = 1 eller 2, annars blir inte talet DCBA fyrsiffrigt. Då HL är jämnt, måste A = 2.
Då är D = 8 eller 9, annars är HL för litet (VL är minst 4*2000). Då 4*D ska sluta på A måste D = 8.

Vi har då 4*2BC8 = 8CB2.

Om vi fortsätter uträkningen med tiotal måste 4*C + 3 sluta på B. Samtidigt får inte B vara för stort (måste vara mindre än 3) för att multiplikationen 4*B00 inte ska ge ett till tusental.

Vi testar med olika C (i uppgiften är det inte givet att siffrorna A,B,C och D är olika även om det brukar vara så i sådana rebusar):

4*C + 3 = (”slutar på”) B
4*0 + 3 = 3 – för stort
4*1 + 3 = 7 – för stort
4*2 + 3 = 1
4*3 + 3 = 5 – för stort
4*4 + 3 = 9 – för stort
4*5 + 3 = 3 – för stort
4*6 + 3 = 7 – för stort
4*7 + 3 = 1 –
4*8 + 3 = 5 – för stort
4*9 + 3 = 9 – för stort

Då vet vi att B måste vara 1 och C är antingen 2 eller 7. Vi testar med båda:

4*2128 = 8512 – passar inte.

4*2178 = 8712 – passar!

Nu räknar vi ut kabelbokstaven:
2178 – 2004 = 174

Tur att man kan lite primtal: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…
Det tionde primtalet är alltså 29.

174/29 = 6 (egentligen hade man kunnat gå från slutet och testat de tio olika ursprungstalen 2004+0, 2004+29, 2004+29*2 och så vidare, men det är lätt att vara efterklok).

Fjärde kabeln ska ha bokstaven (6=)G

Vi var klara med uppgifterna lite innan motståndarbomben smällde (men höll på att kontrollräkna)!

Gillade du för övrigt sifferrebusen, kan du kolla upp några lite svårare här på bloggen: Granrebus, Sifferrebus, Palindromrebus och Trigonometrisk rebus.

Matematik i Genikampen – andra avsnittet

Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte så nu tänker jag göra det.

Flottbygge: Planering och materielinköp

Vi fick 3000 kronor för att handla materiel till vår flotte. Tävlingsledarna skulle kopiera både gula och blå lagets inköp och lagen skulle få de andras inköpta material först. Men i andra omgången skulle lagen få eget material, så det gällde att inte köpa sjukt dåliga saker. Framförallt gällde det att köpa något som man själv skulle ha mer nytta av än motståndaren i samma situation.

Enligt tävlingsreglerna behövde man antingen vinna båda omgångarna för att vinna hela tävlingen eller vinna en av omgångarna med bäst vinsttid (det vill säga, bara tiden för den vinnande omgången räknades). En grej som är lätt att se i efterhand och lite svårare att tänka på innan tävlingen är att det är bara den andra omgången som spelar roll. Givet erfarenhet och att man bygger med eget material tar den andra omgången med störst sannolikhet kortare tid för båda lagen. Det gällde alltså att samla erfarenhet i första och ge järnet i andra omgången.

Under tidspress kunde vi inte vara så värst smarta och planerade en konstruktion som skulle bli alldeles för tidskrävande i andra omgången (så den övergavs). Inne i affären fokuserade vi på att göra beräkningar av typen ”hur mycket volym måste flotten ha för att bära allas vikt?” (blå laget räknade detsamma verkar det som). Fysik i all ära, men ingenjörskonsten med höftning snarare än exakta beräkningar tar ändå alltid priset när det är snabba puckar och inte forskning som gäller.

Andra beräkningar som vi kunde göra skulle då vara hur många hinkar sand flotten skulle kunna bära (förutom oss själva då). Jag kom tyvärr inte ihåg att vi hade fått hinkmått eller mått på lådan vi skulle fylla också, så jag fokuserade på att räkna på kostnaden istället. Tog lite i överkant på varje vara för att inte hamna över (samt för att räkna snabbt) och det slutade med att vi verkligen inte hamnade i överkant, utan hade kunnat köpa typ ett halv toasits till.

Att köpa toasitsar som åror var en briljant idé utav Nina som sparade gula laget mycket tid som annars skulle behövs till åror-tillverkning. Synd att de var så dyra!

Flottbygge: Första omgången

Första omgången gick för båda lagen ut på att samla erfarenhet, framför allt om en bra form på flotten samt om hur många omgångar fram och tillbaka som skulle behövas för att fylla lådan med sand. Vi hade nio hinkar tillgängliga, om jag minns rätt (dock sänkte vi i gula laget en hink i sjön i första omgången). Gula laget hann dumpa sand två gånger, medan blå fyllde hinken på tre gånger! Det betydde att två eller tre gånger skulle behövas i andra omgånger för att vinna hela tävlingen.

Om man skulle åka två omgångar långsamt istället för tre snabbt skulle man ändå vinna tävlingen då tiden att åka fram-tillbaka-fram är tre intervall, medan fram-tillbaka-fram-tillbaka-fram är fem intervall, alltså tar det andra fallet mer än 50% mer tid än det första, om man nu åker med samma hastighet. Tiden det tar att dumpa sand är försumbart i jämförelse med tiden det tar att åka. I programmet hör man att vinsttiden är mer än femtio minuter. Skulle gissa på att max 15 min gick ut på att bygga för blå laget, medan allt annat var rodd (i snitt 7 min per sträcka fram eller tillbaka).

Flottbygge: Andra omgången

Vi i gula laget satsade på att fylla lådan på två rundor, det vill säga åka fram-tillbaka-fram och vinna. Blå laget satsade på samma sak. Viktiga skillnaden för gula laget var att istället för att lägga de 12 frigolitbitarna i fyra lager lägga dem i tre lager. Det betyder att flotten blev till ytan större (4 plattor iställer för 3) och mer stabil (lägre). Det var helt klart den största förbättringen för gula laget gentemot första omgången. En eloge till blå laget som körde på den utformningen av talet 12 redan från omgång ett! I slutändan som det syns i avsnittet var det inställning och småsaker som avgjorde och inte matten. Men utan de idéer som jag nämnt skulle det gula laget varit körda. Tur att det är hög lägstanivå på lagen, så att det inte blir jätteskämmigt när vi spelar genier!

Laser och speglar

Andra tävlingen gick ut på att rikta en laserstråle med hjälp av speglar. Strålen skulle förbi en massa hinder och träffa en ”prisma” (jag tyckte det mera såg ut som en halvklot ihopsatt med en halvikosaeder eller nåt, en prisma ska ha två kongruenta parallella sidor vad jag vet). Tävlingen gick i omgångar; varje omgång bestod av en planeringsfas och en resultatfas. Under planeringen fick man mäta på banan, ställa om och flytta på speglar, göra eventuella beräkningar. Sedan fick man se laserstrålen tändas och en person fick springa fram och göra högst en markering på banan.

Detta syns inte i tv men tävlingen tog hela 14 (!) omgångar. Första omgången träffade gula laget sin första spegel, medan blå laget gjorde inte ens det. Till andra omgången flyttade vi i andra laget andra spegeln lite för att strålen skulle träffa den, men tydligen flyttade vi den lite för mycket! Det var bara på tredje omgången som andra spegeln blev träffad. Och detta var bara speglarna i början, som sattes ut på samma höjd allihopa och med enklar vinklar på 45 grader. Om det var så små marginaler på dem skulle spegelinställningarna i tre dimensioner bli exponentiellt mycket svårare!

Vilket de också blev. Beräkningarna kunde man kasta i papperskorgen och vårt lags strategi var att köra på empiri, det vill säga testa och sedan göra små ändringar. Sedan kan man göra empiri olika bra ocskå. Säg att du ska gissa ett tal mellan 1 och 100 och får veta om din gissning är mindre eller större än det korrekta talet. Då är det bäst att fråga om talet 50 (eller 51). Om det tänkta talet är större, frågar du om 75 och så vidare. På liknande sätt var det för oss när vi ställde in spegelvinklar (både plattformens vinklar och spegelns vinkling): Börja med en gissning, gå sedan ganska långt åt andra hållet (för att definiera en gissningsintervall), sedan någonstans i mitten om man ser att den korrekta vinkeln är mellan de två gissningar, sedan fokusera på rätt halva av intervallet för att få rätt fjärdedel och så vidare.

Detta funkar bra med småvinkeländringar, eftersom, som jag säger i programmet, ”sinus är linjär vid 0”. Det kommer från att
$\lim_{x\to 0} \dfrac{sin x}{x} = 1$ .

Och då även
$\lim_{x\to 0} \dfrac{tan x}{x} = 1$ .

Om markavståndet (dvs avståndet projicerat ovanifrån) från spegelns mittpunkt till nästa spegel är given, så kommer alltså vinkeln bero linjärt på avståndet i den andra ledden (just det vi försöker gissa). Dubblas vinkeln, så dubblas avståndet alltså.

Så för små vinklar funkar det då med samma genomsökningsstrategi som med talen från 1 till 100. T.ex. testar vi med 5-graders vinkeln, sedan med 7 och om strålen ska vara däremellan testar vi med 6 grader (istället för att vara smarta och försöka beräkna att vi ”borde” testa 6,5 eller nåt sånt). Sånt kan ”inte ens jag” beräkna snabbt utan miniräknare och dessutom är det massa felmarginaler på mätningar, så det hade varit meningslöst ändå.

Vi fick instruktioner om att skriva lite smarta saker på tavlan, speciellt under första omgången. Det finns inte jättemycket att skriva när man kör på empiri annat än små anteckningar, så vi roade oss lite istället:

Så klart fanns det annat att tänka på än att bara höfta och ändra inställningar. En viktig sak är hur många speglar man bestämde sig för att använda (man behövde inte använda alla). Ju färre speglar, desto färre lyckade steg man behövde göra. Men å andra sidan skulle varje steg vara något svårare om man skulle försöka ställa in speglarna i 3D (vi kunde ju inte ställa de var som helst, utan bara på några av hindren). Vi körde på strategin ”better be safe than sorry” och jag blå laget gjorde det också, det vill säga använda många speglar med mindre avstånd/svårighetsgrad mellan varje intilliggande par.

En annan sak som jag kom på och var ganska stolt över var att använda flera av de lediga speglarna att ställa på rad för att chansa på att strålen skulle råka träffa nästa spegel också. Lasern bana var mycket värdefull att se och får man se ett steg till ”gratis” var det mycket värt.

Blå laget körde på att titta i speglarna och försöka se prisman i första spegeln. I programmet är jag skeptisk till hur de kunde låta ögat vara så stabilt, men det funkade ju hyfsat bra för dem. Så kanske är det en hållbar strategi ändå! Problemet är att med många speglar multipliceras felet för varje steg. Tänk på när du är i ett rum med massa speglar. Om du flyttar ögat, flyttar de mer avlägsna spegelbilderna mycket snabbare!

Svår tävling var det och krävde mycket tid och energi. Men det var nog min favorittävling i hela Genikampen. Jag gillar att lösa problem när man har ganska god tid på sig. För varje steg fram man kommer får man en kick och vill fortsätta. Dessutom kan man komma på fler och fler strategier som kan testa och föra en fram bättre och snabbare!

Pentago

Duellen gick ut på att spela några omgångar av spelet Pentago, bäst av tre. Duellanterna fick veta reglerna lite innan och provspela ett par gånger. Det finns ju stor risk för missuppfattning, även när man kommunicerar med oss genier ;) Det vore tråkigt om någon gjorde ett olagligt drag i tv eller nåt, även om det såklart svårt att göra det i just det här spelet.

Som i många spel med ett litet spelplan finns det redan beräknat hur man ska spela optimalt. I det här fallet har första spelaren en vinnande strategi, detta behövde dock beräknas med hjälp av en superdator! I massa andra sådana spel är det bevisat att första spelaren har i alla fall en icke-förlorande strategi, som t.ex. ~~i schack (vit kan aldrig förlora om hen gör rätt!)~~ i ”fem i rad” på ett oändligt bräde, men i många sådana spel finns det så många möjligheter att man inte har räknat ut den konkreta strategin. Pentago är rätt litet så det går att beräkna.

Testa att spela och vinna Pentago

Frågan är om man kan lära sig den vinnande strategin utantill, det har jag ju inte försökt mig på. Även om datorn kan göra det på några sekunder, kanske kan det ta en människa veckor för att ”plugga öppningar”. Det hade inte duellanterna. De hade kunnat fokusera på att plugga hur man ”inte gör fel”, t.ex. att man inte ska lägga i hörnen som första spelare och hur man i så fall ska svara som andra spelare. Men jag tror inte det skulle ha hjälpt för att garanterat vinna. Jag tror man kan jämföra Pentago med Othello: Det tar ett tag att bemästra och att lära sig se mönster, men när man väl gjort det så kan man spöa vilken nybörjare som helst. Det var skönt att duellanterna inte hade spelat spelet förut, så att de tävlade på samma villkor.

Jag och Axel fick senare låna spelet och vi försökte komma fram till en vinnande strategi ”för hand” genom att testa olika möjligheter, men jag tror inte vi hann göra det på en halvtimme :)

Matematik i Genikampen – första avsnittet

I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.

Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror att detta har gjort mig smart på flera sätt, inte bara bra i huvudräkning. Matte för mig är så mycket mer än att räkna och därför vill jag visa nedan hur man kan tänka på ett matematiskt sätt även när man inte ”räknar”. Matte för mig handlar om att tänka.

Orientering på sträcka

Tävling ett börjar med att vi blir uppdelade i lag med 6 personer i varje. Uppgiften är att orientera i skogen, det vill säga passera 4 kontrollpunkter innan man kommer fram till målet. Laget får en karta, men ingen kompass. Det gäller att göra detta inte på kortast tid, utan på kortast sträcka! Två personer i laget har GPS-sändare, som sträckan mäts på, men även de andra 4 personerna i laget ska hålla ihop med personerna med GPS, ingen får ”scouta” framme. (Överlag fick deltagarna veta reglerna i detalj och även fick ställa förtydligande frågor, vilket inte visas i tv.)

Jag antar att man tar medelvärdet av de två GPS-positionerna för att få fram banan för att sedan mäta avståndet. Vi fick veta att om avståndet skiljde sig med mindre än 50 m, så var det tiden som gällde. 50 m var så pass lite i sammanhanget (man gick kanske i 35 minuter), så det rätta valet var att strunta totalt i tiden och fokusera på att gå precis kortast.

Hur hjälper matten här då? Jo, man bestämmer att personerna med GPS-sändarna måste gå så rakt som möjlig (DUH!). Detta löser man genom att de inte går först, utan i mitten eller sist. Då kan de personerna som går först gå lite fel (och på så vis ”scouta”). Om personerna som går först går längs med kateterna i en rätvinklig likbent triangel med kateterna 3 m, så kommer personen med GPS:en gå ”bara”

$\sqrt{2}*3 \approx 4,24 m$

4,24 m istället för 6 m alltså! En vinst på 1,76 m! Sker detta 100 ggr, vilket var rimligt för banan, så vinner man redan 176 m på att gå så. Pythagoras sats ftw!

Givetvis är detta egentligen en försumbar optimering i jämförelse med att ”gå rätt”, vilket sätter orienteringsskills över matten i det här fallet. Så är det ibland, men lite bidrag från olika sätt att tänka här och var är sånt som avgör tävlingarna.

Orientering på tid

Andra delen av första tävlingen gick ut på att orientera på ett fabriksområde och hitta halvgömda kontoller. I kontrollerna fanns ledtrådar, mer om dem senare. Här hade gula laget 3 minuters försprång, vilket visade sig inte bara hjälpa, utan stjälpa.

Det fanns nämligen i princip två optimala sätt att ta kontroller (med kortast sträcka): medurs eller moturs (ordningen för kontrollerna blev ganska naturlig), eftersom man skulle tillbaka till samma ställe. Gula laget började, men eftersom blåa laget följde samma riktning, kunde de spara tid på att inte leta efter kontroller, utan observera det gula laget när de var precis ikapp, men lite efter. Det hade blivit annorlunda ifall det blåa laget hade valt motsatt riktning, då skulle förmodligen inget lag få fördel (eller i alla fall är den förväntade fördelen lika) av att vara ”efter”. Banorna skulle korsa varandra i ungefär mitten och då skulle det blivit mer ”rättvisst”. Lite kul ändå att slumpen påverkar!

Uträkningar

Sista delen av första tävlingen gick ut på att göra uträkningar (Genikampen kallar det ”lösa ekvationer”, men jag håller inte med om den termen, eftersom ”ekvationer” för mig förutsätter ett närvaro av ett ”lika med”-tecken och någonting okänt.) Om uppgifterna görs i fel ordning (det vill säga, man försöker få ett resultat utan att veta att KATT = 2 och HARE = 5), så kan man inte få ett svar, men man kan förenkla uttrycken. Gula laget öppnade just ett uttryck med okända först (och visste ju inte vad som väntade), så det enda som fanns i början var att förenkla, vilket gjorde att man kunde räkna ut resultatet av det uttrycket snabbare efteråt.

Som sagt, beräkningar är inte allt som matte är. Nu råkar jag vara snabb på att göra aritmetiska beräkningar, men kanske hälften av de verksamma matematiker jag träffar är inte bra på snabba beräkningar alls. Det är lite som att vara bra på Rubiks kub: Man har antingen lärt sig det eller inte. Man kan vara smart på knep & knåp utan att vara bra på Rubiks kub. Jag skulle inte heller säga att de som är bra på huvudräkning är automatiskt bra på matte, även om man förmodligen är bra på att se mönster, vilket hjälper en att räkna snabbare. Överlag, de som är bra på räkning är personer som är så pass lata att de vill göra det snabbt :)

Testa dig själv på tid om du tycker att det är kul att räkna.

Paintball-quiz

Andra tävlingen gick ut på att ha paintball-dueller med frågesport. Inte jättemycket matte, men man kan fundera över taktiken matematiskt. Det gäller att bedöma sina chanser att träffa vid skjutningen samt chanser att svara rätt på frågan. Om du inte är säker alls på att träffa (t.ex. Valentina som aldrig har sjutit/träffat i sitt liv) bör du skjuta snabbt om det är liten sannolikhet om din motståndare träffar. Med stor sannolikhet missar båda och då har du i alla fall första tjing på frågan. Men det kan också vara dumt att svara först om du t.ex. funderar mellan två alternativ: Då kan det vara bra att motståndaren eventuellt kan utesluta ett av alternativen genom att svara fel. Men den situationen händer typ aldrig.

Om man däremot är bra på att träffa bör man förmodligen börja med att undvika skottet från motståndaren och sedan skjuta själv i lugn och ro. Detta kan ge en säkra poäng, samt chansen att svara först!

Givetvis kan motståndare av liknande ”typ” träffar varandra, vilket resulterar i symmetrisk strategi och en Nash-jämvikt, men det är inget man hinner tänka på när man står där framme :) Då blir det lite kaotiskt och återigen slumpen som avgör.

Ordbygge

Duellen gick ut på att forma ord. Ser man inte färdiga ord så är det brute force som gäller (dvs testa alla möjligheter: Vilken kub är först, vilken är tvåa, hur ska tvåan vara vriden, etc.). Under antagandet att alla bokstäver är unika får vi

$3!\cdot 4^2 = 96$

uppställningar av tre kuber, eftersom kuberna kan ordnas på 6! = 3 sätt och roteras på 4^3 sätt. Men sedan kan varje uppställning ”visas upp” på 4 sätt (genom att ha ett av de fyra orden framme), så därför delar man med 4. Tycker du sånt här med att räkna sätt är skoj, kolla upp en lektion i kombinatorik som jag har lett.

På samma sätt kan man räkna ut att fyra kuber kan ordnas på

$4!\cdot 4^3 = 1536$

sätt och fem kuber på

$5!\cdot 4^4 = 30720$

sätt (under förutsättningen att alla bokstäverna är unika). Antalet sätt halveras ungefär för varje par av likadana bokstäver, men den storleksordningen blir det i alla fall.

Såklart är det mänsikligt omöjligt att testa alla sätt på begränsad tid, men lyckligtvis behöver man det inte, eftersom man kan utesluta massa fall, för att det ska ju bildas ord. Till exempel, om ordet börjar på ett ”T”, så kan inte andra bokstaven vara ”N” och den insikten sparar en 3!*4^3 = 384 fall. Så det var ju mänskligt att lösa det sista pusslet, även om det tog lång tid. Tricket är ändå att se ett ord som är med och anpassa kubuppställningen efter det. För mig var det att se början ”AO” som fick mig att tänka på ”AORTA”, som då senare gav två möjliga uppställningar av kuben, vara den ena var rätt (gav ord även på de andra sidorna: ”LIVET”, ”KENYA” och ”TITAN”).