Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte så nu tänker jag göra det.
Flottbygge: Planering och materielinköp
Vi fick 3000 kronor för att handla materiel till vår flotte. Tävlingsledarna skulle kopiera både gula och blå lagets inköp och lagen skulle få de andras inköpta material först. Men i andra omgången skulle lagen få eget material, så det gällde att inte köpa sjukt dåliga saker. Framförallt gällde det att köpa något som man själv skulle ha mer nytta av än motståndaren i samma situation.
Enligt tävlingsreglerna behövde man antingen vinna båda omgångarna för att vinna hela tävlingen eller vinna en av omgångarna med bäst vinsttid (det vill säga, bara tiden för den vinnande omgången räknades). En grej som är lätt att se i efterhand och lite svårare att tänka på innan tävlingen är att det är bara den andra omgången som spelar roll. Givet erfarenhet och att man bygger med eget material tar den andra omgången med störst sannolikhet kortare tid för båda lagen. Det gällde alltså att samla erfarenhet i första och ge järnet i andra omgången.
Under tidspress kunde vi inte vara så värst smarta och planerade en konstruktion som skulle bli alldeles för tidskrävande i andra omgången (så den övergavs). Inne i affären fokuserade vi på att göra beräkningar av typen ”hur mycket volym måste flotten ha för att bära allas vikt?” (blå laget räknade detsamma verkar det som). Fysik i all ära, men ingenjörskonsten med höftning snarare än exakta beräkningar tar ändå alltid priset när det är snabba puckar och inte forskning som gäller.
Andra beräkningar som vi kunde göra skulle då vara hur många hinkar sand flotten skulle kunna bära (förutom oss själva då). Jag kom tyvärr inte ihåg att vi hade fått hinkmått eller mått på lådan vi skulle fylla också, så jag fokuserade på att räkna på kostnaden istället. Tog lite i överkant på varje vara för att inte hamna över (samt för att räkna snabbt) och det slutade med att vi verkligen inte hamnade i överkant, utan hade kunnat köpa typ ett halv toasits till.

Att köpa toasitsar som åror var en briljant idé utav Nina som sparade gula laget mycket tid som annars skulle behövs till åror-tillverkning. Synd att de var så dyra!
Flottbygge: Första omgången
Första omgången gick för båda lagen ut på att samla erfarenhet, framför allt om en bra form på flotten samt om hur många omgångar fram och tillbaka som skulle behövas för att fylla lådan med sand. Vi hade nio hinkar tillgängliga, om jag minns rätt (dock sänkte vi i gula laget en hink i sjön i första omgången). Gula laget hann dumpa sand två gånger, medan blå fyllde hinken på tre gånger! Det betydde att två eller tre gånger skulle behövas i andra omgånger för att vinna hela tävlingen.

Om man skulle åka två omgångar långsamt istället för tre snabbt skulle man ändå vinna tävlingen då tiden att åka fram-tillbaka-fram är tre intervall, medan fram-tillbaka-fram-tillbaka-fram är fem intervall, alltså tar det andra fallet mer än 50% mer tid än det första, om man nu åker med samma hastighet. Tiden det tar att dumpa sand är försumbart i jämförelse med tiden det tar att åka. I programmet hör man att vinsttiden är mer än femtio minuter. Skulle gissa på att max 15 min gick ut på att bygga för blå laget, medan allt annat var rodd (i snitt 7 min per sträcka fram eller tillbaka).
Flottbygge: Andra omgången
Vi i gula laget satsade på att fylla lådan på två rundor, det vill säga åka fram-tillbaka-fram och vinna. Blå laget satsade på samma sak. Viktiga skillnaden för gula laget var att istället för att lägga de 12 frigolitbitarna i fyra lager lägga dem i tre lager. Det betyder att flotten blev till ytan större (4 plattor iställer för 3) och mer stabil (lägre). Det var helt klart den största förbättringen för gula laget gentemot första omgången. En eloge till blå laget som körde på den utformningen av talet 12 redan från omgång ett! I slutändan som det syns i avsnittet var det inställning och småsaker som avgjorde och inte matten. Men utan de idéer som jag nämnt skulle det gula laget varit körda. Tur att det är hög lägstanivå på lagen, så att det inte blir jätteskämmigt när vi spelar genier!
Laser och speglar
Andra tävlingen gick ut på att rikta en laserstråle med hjälp av speglar. Strålen skulle förbi en massa hinder och träffa en ”prisma” (jag tyckte det mera såg ut som en halvklot ihopsatt med en halvikosaeder eller nåt, en prisma ska ha två kongruenta parallella sidor vad jag vet). Tävlingen gick i omgångar; varje omgång bestod av en planeringsfas och en resultatfas. Under planeringen fick man mäta på banan, ställa om och flytta på speglar, göra eventuella beräkningar. Sedan fick man se laserstrålen tändas och en person fick springa fram och göra högst en markering på banan.
Detta syns inte i tv men tävlingen tog hela 14 (!) omgångar. Första omgången träffade gula laget sin första spegel, medan blå laget gjorde inte ens det. Till andra omgången flyttade vi i andra laget andra spegeln lite för att strålen skulle träffa den, men tydligen flyttade vi den lite för mycket! Det var bara på tredje omgången som andra spegeln blev träffad. Och detta var bara speglarna i början, som sattes ut på samma höjd allihopa och med enklar vinklar på 45 grader. Om det var så små marginaler på dem skulle spegelinställningarna i tre dimensioner bli exponentiellt mycket svårare!
Vilket de också blev. Beräkningarna kunde man kasta i papperskorgen och vårt lags strategi var att köra på empiri, det vill säga testa och sedan göra små ändringar. Sedan kan man göra empiri olika bra ocskå. Säg att du ska gissa ett tal mellan 1 och 100 och får veta om din gissning är mindre eller större än det korrekta talet. Då är det bäst att fråga om talet 50 (eller 51). Om det tänkta talet är större, frågar du om 75 och så vidare. På liknande sätt var det för oss när vi ställde in spegelvinklar (både plattformens vinklar och spegelns vinkling): Börja med en gissning, gå sedan ganska långt åt andra hållet (för att definiera en gissningsintervall), sedan någonstans i mitten om man ser att den korrekta vinkeln är mellan de två gissningar, sedan fokusera på rätt halva av intervallet för att få rätt fjärdedel och så vidare.
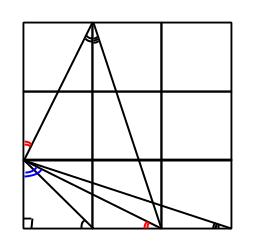
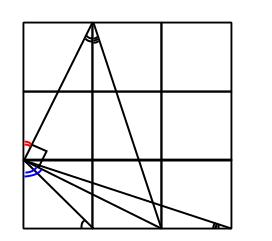
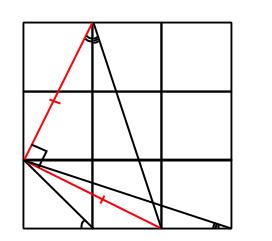
Detta funkar bra med småvinkeländringar, eftersom, som jag säger i programmet, ”sinus är linjär vid 0”. Det kommer från att
.
Och då även
.
Om markavståndet (dvs avståndet projicerat ovanifrån) från spegelns mittpunkt till nästa spegel är given, så kommer alltså vinkeln bero linjärt på avståndet i den andra ledden (just det vi försöker gissa). Dubblas vinkeln, så dubblas avståndet alltså.
Så för små vinklar funkar det då med samma genomsökningsstrategi som med talen från 1 till 100. T.ex. testar vi med 5-graders vinkeln, sedan med 7 och om strålen ska vara däremellan testar vi med 6 grader (istället för att vara smarta och försöka beräkna att vi ”borde” testa 6,5 eller nåt sånt). Sånt kan ”inte ens jag” beräkna snabbt utan miniräknare och dessutom är det massa felmarginaler på mätningar, så det hade varit meningslöst ändå.
Vi fick instruktioner om att skriva lite smarta saker på tavlan, speciellt under första omgången. Det finns inte jättemycket att skriva när man kör på empiri annat än små anteckningar, så vi roade oss lite istället:
Så klart fanns det annat att tänka på än att bara höfta och ändra inställningar. En viktig sak är hur många speglar man bestämde sig för att använda (man behövde inte använda alla). Ju färre speglar, desto färre lyckade steg man behövde göra. Men å andra sidan skulle varje steg vara något svårare om man skulle försöka ställa in speglarna i 3D (vi kunde ju inte ställa de var som helst, utan bara på några av hindren). Vi körde på strategin ”better be safe than sorry” och jag blå laget gjorde det också, det vill säga använda många speglar med mindre avstånd/svårighetsgrad mellan varje intilliggande par.
En annan sak som jag kom på och var ganska stolt över var att använda flera av de lediga speglarna att ställa på rad för att chansa på att strålen skulle råka träffa nästa spegel också. Lasern bana var mycket värdefull att se och får man se ett steg till ”gratis” var det mycket värt.
Blå laget körde på att titta i speglarna och försöka se prisman i första spegeln. I programmet är jag skeptisk till hur de kunde låta ögat vara så stabilt, men det funkade ju hyfsat bra för dem. Så kanske är det en hållbar strategi ändå! Problemet är att med många speglar multipliceras felet för varje steg. Tänk på när du är i ett rum med massa speglar. Om du flyttar ögat, flyttar de mer avlägsna spegelbilderna mycket snabbare!
Svår tävling var det och krävde mycket tid och energi. Men det var nog min favorittävling i hela Genikampen. Jag gillar att lösa problem när man har ganska god tid på sig. För varje steg fram man kommer får man en kick och vill fortsätta. Dessutom kan man komma på fler och fler strategier som kan testa och föra en fram bättre och snabbare!

Pentago
Duellen gick ut på att spela några omgångar av spelet Pentago, bäst av tre. Duellanterna fick veta reglerna lite innan och provspela ett par gånger. Det finns ju stor risk för missuppfattning, även när man kommunicerar med oss genier ;) Det vore tråkigt om någon gjorde ett olagligt drag i tv eller nåt, även om det såklart svårt att göra det i just det här spelet.
Som i många spel med ett litet spelplan finns det redan beräknat hur man ska spela optimalt. I det här fallet har första spelaren en vinnande strategi, detta behövde dock beräknas med hjälp av en superdator! I massa andra sådana spel är det bevisat att första spelaren har i alla fall en icke-förlorande strategi, som t.ex. i schack (vit kan aldrig förlora om hen gör rätt!) i ”fem i rad” på ett oändligt bräde, men i många sådana spel finns det så många möjligheter att man inte har räknat ut den konkreta strategin. Pentago är rätt litet så det går att beräkna.
Testa att spela och vinna Pentago
Frågan är om man kan lära sig den vinnande strategin utantill, det har jag ju inte försökt mig på. Även om datorn kan göra det på några sekunder, kanske kan det ta en människa veckor för att ”plugga öppningar”. Det hade inte duellanterna. De hade kunnat fokusera på att plugga hur man ”inte gör fel”, t.ex. att man inte ska lägga i hörnen som första spelare och hur man i så fall ska svara som andra spelare. Men jag tror inte det skulle ha hjälpt för att garanterat vinna. Jag tror man kan jämföra Pentago med Othello: Det tar ett tag att bemästra och att lära sig se mönster, men när man väl gjort det så kan man spöa vilken nybörjare som helst. Det var skönt att duellanterna inte hade spelat spelet förut, så att de tävlade på samma villkor.
Jag och Axel fick senare låna spelet och vi försökte komma fram till en vinnande strategi ”för hand” genom att testa olika möjligheter, men jag tror inte vi hann göra det på en halvtimme :)

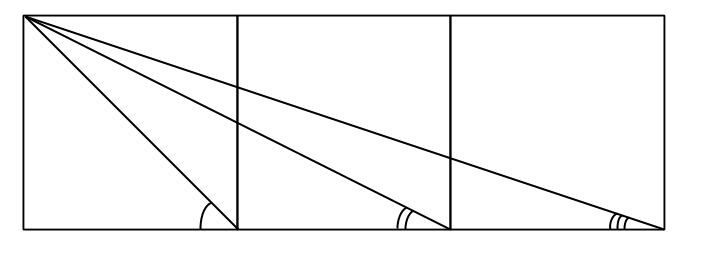
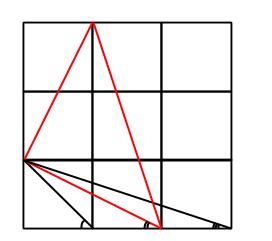
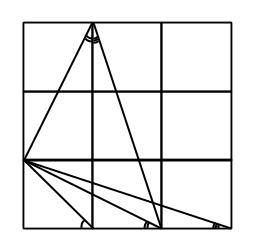

 eller
eller De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.