Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Grafer
Jag försökte att introducera grafer på den allra första lektionen men begreppen tog sig inte. Det var inte naturligt för fem- och sexåringarna att representera människor med prickar och syskonsrelationer med pilar. Eller så passade inte temat till att vara först av alla helt enkelt.
Därför tänkte jag prova igen att bekanta barnen med grafer, denna gång med en mycket mjukare introduktion. Därför handlar egentligen inte så stor del av lektionen om grafer.
Barn ska kunna differensiera enkla linjära former
Titelt är ett skämt och betyder ungefär att barn ska kunna skilja på cirklar, trianglar och kvadrater.
Dagens lek går ut på att bygga ett land som består av öar. Öarna har alla olika färg och form: cirkel, rektangel, ring, femhörning etc. Barnen ska kunna nämna alla formerna. Vi placerar öarna på ett stort blått papper som symboliserar havet.
Broar
För att öarna ska bilda ett rike, måste det finnas sätt att ta sig emellan dem. Barnen får en bro i taget (en platt avlång rektangel), som kan förbinda två öar med varandra. Vilket är det minsta antalet broar som behövs för att man ska kunna promenera runt hela landet?
När vi har byggt det minsta antalet broar som krävs för att landet skall vara sammanhängande (vilket är 1 mindre än antalet öar). Hur många broar till kan vi bygga, om inte två broar får korsa varandra (broarna får vara böjda)? På den sista frågan vet inte jag det exakta svaret. Tillsammans med barnen ska vi i alla fall hitta ett lokalt maximum, det vill säga en situation där ingen ny bro kan sättas in, hur den än slingrar sig, på grund av korsandet av andra broar.
Köningsbergs broar
Man bestämde sig för att måla om alla broarna i landet till en ny färg. Går det att köra med målarbilen exakt en gång på varje bro? Det vill säga aldrig köra på en och samma bro två gånger och inte heller utelämna någon bro.
Barnen får göra minst ett försök var. Det tar ett tag innan man hittar den rätta vägen, om den nu existerar!
Detta är samma problem som Köningsbergs broar. Bara formulerat lite annorlunda.

Rita utan att lyfta pennan
För de äldre barnen passar uppgiften: rita figuren utan att lyfta pennan från pappret medan du ritar.
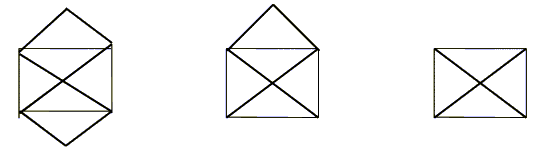
Auktion
Varje barn får ett och samma antal pappersmynt. De får i hemlighet bjuda ett visst antal mynt på varje ö. Den som bjuder flest mynt, får bli öns president (om det är lika, bjuder man om). Mynten man har kvar, kan man spendera på byggblock, som man får bygga presidentpalatset av på sin ö.
Detta lär barnen hur en bjudning kan fungera. Också lär de sig att snabbare jämföra antal och avgöra vem som bjöd flest mynt.
Karta
Det är dags att rita landets karta! Rita av landet på ditt eget papper. Du kan börja med ön där du är president och rita resten därifrån.
Samtidigt som barnen ritar jag en ”karta” där öar bara är prickar och broar är streck. Sedan får barnen se kartan. Kan alla peka på sin egen prick?
Flaggor
Landets färger är blått (havets färg), gult (solens färg) och rött (broarnas färg). Vi vill att landet inte bara ska ha en flagga, utan alla möjliga randiga flaggor som består utav 1, 2 eller 3 ränder!

Barnen får tillsammans måla alla flaggorna och kontrollera att de ha tagit alla kombinationer. Eventuellt kommer de på att man kan ha ränderna på det andra hållet (som i den rumänska flaggan och inte den ryska). Om ränderna är som på bilden ovan, finns det 15 olika flaggor man kan göra.
Set
Om det blir tid över, spelar vi set med de äldre barnen. På spelet står det att lägsta åldern är 6, men jag tror att det är meningsfullt att köra spelet först vid 7.
