I helgen har Sonja Kovalevsky-dagarna varit i Stockholm för andra året i rad. Och fjärde året i rad har jag hjälpt till med problemlösningsdelen :)
Här är tävlingsproblemen och lösningar för de intresserade.
Tips inför SMT-final
Som vanligt lite sent kommer det några tips inför morgondagens tävling! De allmäna tävlingstipsen gäller förstås fortfarande.
Saker som är bra att kunna inför finaltävlingen utöver det man ska kunna inför kvaltävlingen:
– Triangelolikheten
– Största sida ligger mittemot största vinkeln i en triangel, minsta mittemot minsta
– Bisektrissatsen och förhållandet i vilken medianernas skärningspunkt delar medianerna
– Homoteti och inversion (om du är proffs och kan allt annat :))
– Linjens ekvation
– Vad polynom är för något, faktorisering och division med rest
– Grundläggande sannolikhetsteori
– Diofantiska ekvationer
– Grundläggande kombinatorik
Bevistekniker som är bra att kunna inför tävlingen:
– Induktion
– Insättning av specialfall i funktionalekvationer och härledning av fukntionens egenskaper (jämn, udda, linjär, kvadratisk etc.)
– Invarianter och halvinvarianter
Problemen i finalen är svåra, men det handlar framför allt att komma på finurliga lösningar och inte särskilt mycket om att kunna matematiska termer. Mitt största råd är att koncentrera sig på problemen där man har fullt koll på matematiken. Försök på alla problemen litegrann, men försök seriöst på ungefär fyra av problemen. Ibland krävs helt enkelt en timmes koncentration för att komma på en lösning!
Och sist men inte minst: lycka till!!!!!
Logiskt tänkande med små barn: träff 5 och 6
Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de föregående träffarna:
1 & 2
3 & 4
eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla lektioner.
Geometri för barn
De senaste gångerna har vi fortsatt att öva på geometri, nämligen att rita linjer. Boken hade några övningar på linjer man skulle rita av och barnen fick i princip välja bild själva.
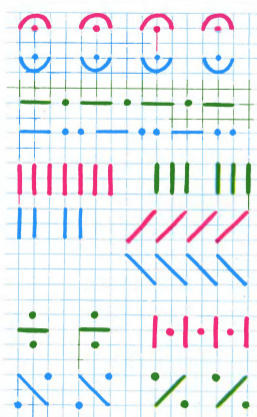
Några få lyckades kopiera bilderna skalenligt, de flesta behöll formen men gjorde själva bilder i större skala än originalet.
Stjärnbilder
För att fortsätta öva på att använda linjal försökte jag komma på en uppgift där barnen skulle sammanbinda punkter med linjer. Till slut slog det mig: stjärnbilder!
Jag skrev ut 12 stycken osammanbundna bilder:
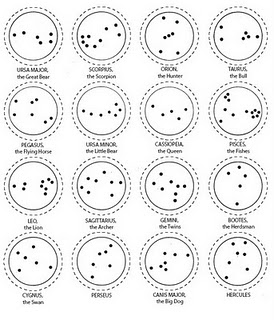
Först pratade vi om himlen och vad man kan se där under natten. Sedan fick varje barn en sådan lapp tilsammans med en liten linjal, samtidigt som jag visade en bild där någon hade sammabundit punkterna utan linjal (jag gjorde det själv i paint). Jag försökte trycka på att det såg så fult ut, men att de skulle minsann kunna göra ett bättre jobb tillsammans med sina linjaler. Men jag tror inte riktigt den fula ”bilden” gav någon effekt.
Barnens egna fantasi satte igång och de började hitta på egna bilder (”stjärnbilden robot”, ”stjärnbilden cirkus”) och de upptcäkte efter ett tag att gick snabbare att rita linjerna utan linjal och det blev snyggt ändå.
Det blev ett rättvisst misslyckande, för man ska ju inte använda linjal när man inte egentligen behöver, och barnen förstod det. Nästa uppgift med linjaler bör innehålla långa sträckor.
Hur som helst hade barnen mycket skoj då de hitta på egna varianter av sjtärnbilder. Själv lärde jag mig några nya konstellationer och kan numera känna igen något annat än Karlavagnen och Orion på natthimlen. Jag hoppas att barnen kan göra det också. Stjärnpositionerna var ju desamma i deras bilder som på himlen, sammanbindningen spelar ju ingen roll.
Höger och vänster
Några av uppgifterna i geometriboken handlade om höger/vänster och över/under, så varje barn fick en fråga på det.
Jag tycker att det är viktigt att varje barn får chans till en egen fråga, så att han eller hon blir hörd (och förhörd), men det finns ett problem med de andra barnen. Vad ska de göra under tiden? Om de får lyssna på frågan, vill de blanda sig i och svara istället för den tillfrågade. Om de inte får lyssna, har de istället tråkigt. Det gäller nog att tilldela barnen sin egen uppsättning av objekt och/eller uppgifter, så att de kan koncentrera på och leka med det som är framför dem. Jag ska nog trycka upp uppgifterna i flera exemplar nästa gång.
Då jag märkte att barnen var osäkra på vänster/höger, lekte jag några lekar med dem som handlade om det. Vi brukar sitta runt ett bord, så jag bad alla att peka på sin högra granne (så att alla blev pekade på, om det fanns tomma stolar, ignorerade vi dem), sedan på sin vänstra granne. Räcka upp sin högra hand, trampa med sin vänstra fot etc. Många barn har fortfarande svårt för höger och vänster, men de vet nu i vilket fall att det är en relativ riktning.
Jag ställde även svåra frågor till barnen, t.ex. ”Vem är Karolinas vänstra granne?” (frågan ställs till någon annan än Karolina). Svaren var oftast rätt trots att frågorna kan vara förvirrande om t.ex. barnet i fråga sitter mitt emot och man måste tänka på hans eller hennes vänster istället för sitt eget.
Laglekar
Som tidigare behöver gruppen jag har kring lunch att röra på sig i början av lektionen. Jag försöker variera lekarna.
Under träff 5 fick de springa över klassrummet till ett bord med olika tärningar, springa tillbaka och slå den. Om det blev en etta fick de poäng. Sedan skulle de upprepa proceduren, fast denna gång med en ny tärning. Alla var ett lag tillsammans och det gällde att få 10 poäng på snabbast tid. De var sex stycken och de klarade det på drygt 1 minut (klassrummet var ganska långt)!
Pojken med den sista ettan tyckte att han vann förstås, men jag försökte poängtera att de tävlade som ett lag. Jag skrev även deras tid med stora siffror på en A4 och sa att det var deras rekord.
Under träff 5 lekte de emellertid som två lag (tre barn i varje). Jag placerade ut alla brickorna till Färgkoden (se tidigare inlägg) på stolarna i klassrummet och det gällde för laget att hitta de tre brickorna de behövde till deras egna bild. Och sedan sätta ihop bilden så snabbt som möjligt. Brickorna som inte tillhörde något av lagen skulle de ge till mig.
Lagen hittade brickorna ungefär samtidigt, men ena laget fick något lättare pussel tror jag och de klarade det något snabbare också (och då vann).
Para ihop kinesiska tecken
Tidigare försökte jag få barnen att para ihop likadan figurer, men jag hade för svår nivå på figurerna. Länge försökte jag komma på vad jag skulle ha för bilder som vore skoj att bara ihop (det skulle inte vara för enkelt och inte heller för svårt).
Till slut bestämde jag min för kinesiska tecken. För en nybörjare är de ganska lika sinsemellan. Men tittar man noga, ser man skillnaderna. Jag berättade för barnen att vi idag inte skulle lära oss kinesiska, utan bara hitta par av likadan tecken. Varje tecken på vänstra halvan av pappret hade ett par i den högra sidan av pappret.
Jag tror att 20 par blev lite för mycket. Ungefär 15 barn fick den här uppgiften och jag tror att bara två blev klara innan några andra barn i gruppen blev uttråkade (då brukar jag avsluta en aktivitet).
Slå in en kub
Inte alla figurer som består av 6 rutor funkar som omslag till en kub. Det finns egentligen många fler som inte funkar än de som funkar.
Jag förberedde några små sanna och falska omslags som barnen fick testa på tärningar. Ifall alla tärningens sex sidor täcktes fick barnet behålla omslaget (om få barn deltog i leken, fick de behålla flera stycken som ”poäng”). De falska omslagen, som täckte fyra eller fem sidor (och således någon sida blev dubbeltäckt) skulle kastas bort. När alla omslag hade testats, hade alla barn fått var sitt unikt omslag. Då fick de komma fram till bordet där stora omslag (storleken passade till en Rubiks kub) låg framme, alla i olika färger. Bland de stora fick de hitta sitt eget (lite träning i likformighet!). Några hittade sin form snabbt, om det såg speciellt ut, som bokstaven T till exempel. Andra hade det svårare då de var tvungna att ibland vända på sin egen figur upp och ner eller rotera den för att hitta en stor figur med samma form. När alla hittade var sitt stort omslag, slog vi in Rubiks kub i sju stycken olikafärgade omslagspapper. Det blev väldigt vackert!
Jag är ganska stolt över den här uppgiften. Barnen tyckte om det vackra resultatet på slutet och att de var delaktiga i processen. Genomförandet kan bli lite stökigt om några barn blir klara mycket snabbare än andra, men man kan lösa detta genom att ropa fram dem en och en till det stora bordet, allt eftersom de blir klara.
Röra på sig lite
Efter en rekommendation från en annan lärare, som sade att små barn inte hade fysiologi nog att sitta stilla i mer än 20 minuter, har jag sett till att de rör på sig i mitten av lektionen, åtminstone i en halv minut. De senaste gångerna har jag kört med en dikt på ryska, där barnen ska upprepa rörelser efter mig.
Den översätts ungefär så här:
Ett – ställ dig upp och sträck upp armarna
Två – böj dig ner och sen sträck på dig
Klappa händerna tre gånger
Nicka tre gånger
På fyra sträck ut händerna
Fem – vifta med händerna
Sex – sätt dig tyst på din plats
Det rimmar på ryska och är en jättebra ramsa, då barnen faktiskt sätter sig ner väldigt tyst på slutet.
En ska bort
Ett viktigt begrepp att lära sig i 5-6 års åldern är klassificering. Sen skadar det inte om barnen börjar resonera. Dessutom är det viktigt i matten att lära sig att det kan finnas fler än ett rätt svar.
En perfekt kombination av alla dessa saker är leken ”en ska bort” (eller ”den fjärde är annorlunda”). En bild med fyra föremål visas och man ska säga vilket det är som skiljer sig från de andra. Och sedan förklara varför.
På bilden ovan finns åtminstone två rimliga svar: ballongen (de andra är insekter) och larven (den kan inte flyga). Oftast ger barnen det mest uppenbara svaret, men ibland kommer något icketrivial som i fallen med en hund, en anka, en höna och en gås. Svaret blev hönan, för att den inte kunde simma.
Alla alternativa svar uppmuntrades av mig, om de hade en förklaring. Om förklaringen inte riktigt funkade ställde jag en motfråga (t.ex. är det verkligen så att musen inte är ett husdjur?). Jag körde igenom 10 bilduppsättningar, några blev personliga och några fick barnen lösa tillsammans (eller den som först kom på något svar fick prata först också).
Vilka är fler?
Inspirerad av pedagogen Zvonkin (som i sin tur hämtade idéerna från utvecklingspsykologen Piaget) testade jag mängdbegreppet på barnen. Jag ställde upp två rader med pjäser, blåa mittemot gula (9 stycken var). Jag kallade dem för soldatarméer och frågade vilka skulle vinna. Av någon anledning hade barnen färgpreferenser och tyckte t.ex. att de blå skulle vinna. Sedan tog jag bort en av de blåa soldaterna och frågade vilka som nu skulle vinna. Förstås vad svaret nu ”gula”.
Sedan kommer någonting förvånande, men som jag väntat mig efter att ha läst boken. Jag drar ut raden med blåa soldater (så att det blir större avstånd dem emellan) så att den blir lika lång som den gula. Vilka vinner nu?
”Ingen!”, svarar barnen. För dem finns det lika många blå som gula eftersom de bildar lika lång rad. Jag upprepar proceduren och tar bort fler och fler blå soldater. Till slut (när det finns 2-4 blå pjäser kvar) märker de att något är på tok. Nu påstår de att gula faktiskt vinner. ”Varför?”, frågar jag och får förklaringen att det faktiskt nu finns långa tomrum mellan de blåa pjäserna. En gul pjäs kan få plats där.
Det ska bli kul att se när begreppet antal bli skilt från mängdbegreppet, så att barnen märker även på första steget att soldaterna inte är lika många.
6 bitars-pussel
Jag har några mjuka pussel, där man egentligen ska bygga en kub av 6 bitar. Men att lägga dem tillbaka i ramen är inte trivialt heller. Jag har bara 4 stycken sådana pussel, så bara barnen i din lilla gruppen fick leka med dem tyvärr. Ska skaffa fler när jag får chansen!
Pusslen är trevliga att hålla på med, för bitarna är stora och färgglada. De är rekommenderade från 7 år och jag skulle nog hålla med rekommendationen. Barnen klarade att lägga dem men bara med min hjälp (i de flesta fallen). Jag sa åt barnen att man inte bara kunde lägga in bitarna utefter form, men också utefter mönster (man kan se på kantgränserna ifall mönstret fortsätter som det ska). Men mönstret är inte jättetydligt så det var svårt för dem att följa det.
Det lite tråkiga med sådana uppgifter är att man ska sitta själv och hålla på med det. Om jag organiserar en sådan aktivitet vill jag ha tillgång till många pussel samtidigt, så att varje barn kan ha något att göra om han eller hon blir klar.
Film
Vi fortsatte att kolla på tv-serien. Vi såg ett 9-minuters avsnitt som handlade om på vilket sätt talen från 1 till 20 består av siffror. Egentligen handlade det om att bosätta passagerare i deras hytter på ett skepp och hur man skulle göra för att var och en visste vart man skulle gå. Givetvis blev det missförstånd på slutet, då två av passagerarna tyckte att de fick likadana biljetter (en lapp med ett tal på). Kan du gissa vilka nummer det var på deras hytter? :)
Logiskt tänkande med små barn: träff 3 och 4
Jag fortsätter mina lektioner med små barn i Stockholm. Läs om de första två träffarna eller fortsätt läsa det här inlägget. Notera att ordningen inte är kronologisk och att inte alla aktiviteter förekommer på alla lektioner.
Geometri för barn
Det vore svårt för mig att föra lektioner utan att ha någon litteratur som bas. Jag gjorde ett nytt försök denna gång att använda mig av en bok riktad till små barn som handlar om matte. Denna gång var det ”Geometri för de minsta” av V.G.Zhitomirskiy och L.N.Shevrin, en bok som gavs ut 1975 i Moskva.
Boken är riktad till förskolebarn och lär ut begrepp som punkt, linje, triangel etc. med hjälp av en levande berättelse. Jag läser berättelsen för mina barn och gör några av övningarna som finns i boken (samtidigt som karaktärerna i boken, lär vi oss att rita olika linjer, bl.a. räta med hjälp av linjal). Tanken är att barnen ska bli bekanta med geometriska objekt och samtidigt övar på att framställa dessa.
Det här bokexperimentet har börjat väldigt bra. Jag kör geometrin i början av timmen, och barnen verkar vara sugna på att göra uppgifterna. Efter ett bra tag (10 minuter är väldigt lång tid i sammanhanget för att hålla på med en och samma sorts uppgift) börjar de hitta på egna saker att rita, helt enkelt för att de är sugna på att rita.
I början hade jag med tuschpennor, men då de förstörs lätt om barnet trycker för hårt, har jag börjat köra med vanliga (blyerts-)färgpennor. Viktigt är dock att dela ut välfungerande penna med synlig färg till varje elev.
Klappar
Klappleken är något jag gärna kör med mina vuxna vänner. Den går ut på att man sitter runt ett bord och alla deltagarna lägger fram båda händerna på bordet.
Kort och gott handlar det om att man ska klappa rätt hand i rätt tid. ”Klappen” börjar med någons hand och sedan ska alla händer klappa en gång i tur och ordning (medsols till exempel). Någon hand kan genomför en dubbelklapp och i så fall byter man riktning. Klappar någon vid fel tillfälle eller är väldigt försenad med klappen när hon eller han faktiskt ska klappa, förlorar den personen en hand (vi hugger inte av handen, utan bara tar bort den från bordet). Man spelar tills det är 2-3 personer kvar och då har de vunnit.
Möjligen var det för tidigt att köra leken med de sexåriga barnen. Jag tror inte alla reglerna var självklara, dessutom vill några av barnen förstås fuska (att inte ta bort handen när man gjorde fel), vilket sabbade leken för alla andra. Det är möjligt att barnen uppfattade att de skulle härma mina rörelser (jag klappade med högra handen först och sedan vänstra), men för barnen mittemot blev ordningen fel om de försökte spegla mig.
Para ihop krångliga figurer
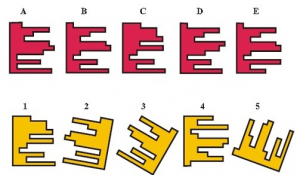
Jag hittade en uppgift på nätet där krångliga figurer skulle paras ihop, om de hade exakt samma form. Varje person fick en egen lapp med figurerna, men för de allra flesta gick det inte att se så mycket skillnader. Jag hjälpte till då genom att klippa ut de gula figurerna så att de i tur i ordning kunde läggas på röda och jämföras, vilket hjälpte några av barnen, men långt ifrån alla.
Jag tror uppgiften är bra, men något enklare figurer nästa gång!
Siffersallad
Jag hade några blanka vita kort som kom till användning. På varje kort skrev jag fyra siffror, varje siffra i egen färg, t.ex. 2 3 7 0.
Siffersallad är en lek där idén är hämtad från leken ”fruktsallad”, en lek för att grupp människor ska byta plats och samtidigt lära känna varandra. I vårt fall blev reglerna så här: jag ropar ut en siffra, och alla barn som har den siffran på kort ska gå från sin plats och sätta sig på en annan. T.ex. säger jag 7 så byter alla som har siffran 7 plats, medan alla andra sitter still.
Det var viktigt att fråga alla barnen, innan leken började, vad de hade för siffror på sitt kort, vilket jag tyvärr inte gjorde alla gånger. Under leken fick jag frågor vad vissa siffror var, några undrade t.ex. om nian var en sexa.
Många tyckte om att gå upp och röra på sig, så de ville också ropa ut siffror. Jag lät varje barn ropa ut en siffra och de tog givetvis en av siffrorna på kortet. Några enstaka gånger sades två siffror (”de som har 4 eller 5 byter plats), jag vill långsamt ut lära ut konceptet ”matematiskt eller” till barnen.
Knuten
En annan fysisk lek är knuten. Alla barnen ställer sig en ring, sträcker fram båda armarna och blundar. Sedan går de framåt och med varje hand ska de greppa en annan hand. När handgreppandet är klart, får de öppna ögonen. Nu får de inte släppa taget, utan måste lösa upp den ”knuten” som har bildas. Man får vända på sig, går över de andra barnens grepp, gå under greppet etc. Ibland består den upplösta knuten av flera människoringar (kan också hända att vissa personer måste stå bak och fram i slutändan).
De barnen som var med tyckte det var en rolig lek. Femåringarna hade svårt med reglerna om att man skulle ta tag i nån annans (lediga) hand utan greppade bara i någons axel eller redan upptagna handtag, så jag fick styra dem lite. Kanske ska jag nästa gång bestämma själv hur de ska hålla varandra i händerna och på så sätt garantera mig om att få en knut.
Det var synd att inte alla barnen ville vara med löken, de kanske tyckte att det var suspekt med fysisk kontakt, eller hade nåt emot att ställa sig i en ring. Då blev leken mycket enklare och snabbare för de barn som var kvar. Det är roligast att köra om 5 eller fler barn deltar.
Spel
Jag tog med ett tyskt spel, egentligen för att de spela med de äldre barnen (tioåringarna). Men vi spelade det även med några av sexåringarna i eftermiddagsgruppen. Alla barnen som testat att spela det var väldigt förtjusta i att spela, även om de inte hade lyckats vinna.
Jag tror att spel är ett väldigt bra sätt att utveckla barnens tänkande och vissa färdigheter. Just det här spelet är rekommenderat från 8 år. Man ska kunna ha bra koll på siffrorna från 1 till 15, samt kunna jämföra dem. Och för att vinna ska man även kunna ha koll på andra spelare och försöka komma ihåg ifall de har använt sina bästa siffror redan eller inte.
Det kan hända att jag kommer tillverka en förenklad version av spelet för fem- och sexåringar. Viktigt är att det ska vara enkelt för dem att hålla i korten, ha översikt överhanden och så ska reglerna inte vara så svåra förstås.
Fysisk övning
Sexåringarnas förmiddagsgrupp kommer till mina lektioner utan att ha någon egentligen rast innan. Lektionen före är ryska och de sitter i princip stilla under en timme. Tillsammans med föräldrarna har jag kommit fram till att det är nödvändigt för barnen att röra på sig (”springa av sig”) under kontrollerad form i början av lektionen.
Så under träff fyra började vi med att hitta på rörelser och utförde dem. T.ex. klappa en gång, stampa två gånger, nicka tre gånger etc. Varje barn fick en siffra och kunde hitta på en egen rörelse. Vi körde från 1 till 10 och möjligtvis blev leken för lång i och med 10 varv runt bordet. Men spring under 2 minuter ungefär tror jag blir optimalt nästa gång.
Rymden
Ett av barnen berättade för mig att han tyckte om rymden och ville att vi skulle ta upp det på lektionerna. Jag försökte göra en uppgift för alla, som skulle använda sig av logiskt tänkande.
Jag skrev ut en bild på Jorden och några atmosfärlager runt den. Dessutom hade jag små bilder på objekt i rymden/himlen: en raket, en asteroid, ett flygplan, en ballong och en rymdstation. Uppgiften var att placera ut objekten på bilden beroende på deras relativa avstånd från Jorden.
Barnen tyckte om bilderna, men uppgiften blev lite luddigt formulerad. Dessutom är det svår att placera ut t.ex. raketen på rätt sätt – den kan väl vara på jorden eller precis lyft eller jättelångt bort? Men barnen förstod att ballonger och flygplan var nära Jorden och det är väl det viktigaste.
Jag berättade om att asteroider kunde falla ner på Jorden och
det tyckte barnen var lite häftigt tror jag.
Bygga labyrint
Jag berättade om spelet Färgkoden i förra inlägget. Labyrintspelet kommer från samma tillverkare. Det går ut på att arrangera 9 brickor, som har vägar på sig i ett vägnät. På utkanten av spelplanet finns bilder (äppelträdet, räven, haren, farmor etc.) Vägen ska se ut på så sätt att det ska vara möjligt för vissa av figurerna att komma fram till andra.
Spelet är långt ifrån trivialt och även de enklaste uppgifterna kan vara svåra att lösa. Barnen tycker om att försöka lösa uppgifterna, men tyvärr är det svårt att leka mer än en samtidigt. Är någons tur att leka får de andra hjälpe honom eller henne, men det slutade ofta med att det mer dominanta barnet tar över och börjar lägga brickorna.
Jag kommer ta med spelet när vi har ”pusselstund”, där varje barnen kan få eget spel eller pussel att sysselsätta sig med. På fjärde träffen uppstod en sådan stund naturligt i några minuter, då de nyfikna barnen gick runt och snokade efter vad jag hade med mig för någonting. Givetvis hittade de ofta något pussel och började leka med det spontant och då känns det helt fel att stoppa dem.
Film
I slutet av träff fyra kollade vi på en liten film med sexåringarna. Det är ett amerikanskt program för barn (duh), där sifferfamiljen (Number Crew) sköter ett skepp med många djurpassagerare. Under resans gång lär man sig att räkna och använda siffror.
Barnen satt som klistrade till stolarna när jag satte på filmen på datorn. Jag tror inte någon av dem var ouppmärksam ens en sekund :) Perfekt aktivitet för mig att köra på slutet av lektionen då jag kan plocka ihop alla andra pussel.
Filmerna skulle nog inte passa alla femåringarna. De innehåller räkning till 20 redan i första avsnittet, så det kan eventuellt bli för mycket på en gång för de som inte kan räkna till 10 än.
Läsa berättelse
Jag fortsätter läsa berättelsen om Kubarik och Tomatik, men endast för de femåriga barnen. Jag borde verkligen göra berättelsen mer interaktiv, så att de blir roligare för barnen att lyssna. En av träffarna handlade sagan om vad som hände på natten, så jag började med att fråga ut barnen först om hur man visste att det var natt just nu. Jag bad de även att rita natt. Då sattes de in i berättelsen bättre.
Jag ville tro att mina lektioner blir bättre nu när jag lär känna de olika barnen och deras behov lite bättre. Mina grupper är verkligen olika och det spelar stor roll vilken tid på dagen det är. Samtidigt har barnen träffat mig några gånger nu och vågar vara sig själva, nu när de sett att jag är snäll :)
Var kommer talet e ifrån?
Jag hade själv länge ingen intuitiv förståelse för 
Tills jag träffade på sidan som förklarar svåra begrepp på ett intuitivt sätt. Sidans författare gick snällt med på att dela med sig av sin förklaring och bilder. Utav det gjorde jag en presentation om talet
Skriv gärna om förklaringen hjälpte dig att förstå
Tips inför SMT-kval
Nu är det bara några timmar kvar till SMT-kval och jag tänkte dela av mig med mina tävlingstips.
Allmänna tävlingstips:
– Ha skoj! Det här är bara en tävling.
– Slösa inte bort tiden, fem timmar kan gå väldigt fort! Gör ett gott försök att lösa varje problem, men spendera inte mer än en halvtimme om du inte kommer nånvart.
– Läs problemtext noga. Det är bättre att ställa en fråga till läraren än att försöka lösa ett annat problem än det som står.
– Om du tror att du har löst uppgiften, läs texten noga igen. Skriv ner lösningen direkt. Eventuella fel eller obevisade påståenden brukar dyka upp först när du skriver ner resonemanget.
– Bara ett svar ger oftast 0 poäng, men en ofullständig lösning kan ge upp till 6. Skriv alltså ner alla idéer du har på problemen tydligt. Om du har en plan för lösningen, men inte kan bevisa alla stegen, skriv ner planen.
När du inte har någon aning om hur du ska lösa uppgifterna, finns det några olika tekniker du kan prova:
– Undersök ett enkelt fall av problemet. T.ex., om det handlar om en 8×8-kvadrat, prova att göra samma sak med en 4×4-kvadrat eller även 2×2.
– Kolla specialfall. Svaren kan t.ex. vara olika för jämna och udda n. Prova att sätta in några tal och se om du upptäcker samband eller mönster. Om det är en funktionalekvation, stoppa in 0 iställer för x och sedan ocskå 1, -1, 2, -2, -x.
– Är det en geometriuppgift, rita figuren så nogrannt som möjligt! Då kan du t.ex. ”se” vad svaret ska bli för något. Och om du vet svaret, t.ex. att en vinkel ska vara lika med 45 grader, blir det lättare att bevisa det.
– Kom ihåg att olika bilder kan uppstå i geometriuppgifter. Ett missat fall (t.ex. en punkt ligger inuti en cirkel och du har bara kollat när den är utaför eller på) kan ge avdrag.
– Att rita en bild underlättar även lösning av uppgifter, som inte är geometri.
– Anta saker ”utan inskräkning” så att det blir lättare att jobba med problemet. T.ex. i en olikhet som är symmetrisk med avseende på a, b och c (det vill säga att man kan byta plats på två av bokstäver och olikheten förblir densamma) kan man anta att a>=b>=c.
Lite saker bör du kunna för att lösa många av uppgifterna:
– Hur man faktoriserar tal i primtal. Delbarhetsprinciperna för 2, 3, 4, 5, 9 och 11.
– Uppställning för aritmetik för tal i bas tio (dvs talteoriproblem som handlar om siffror löses med att kolla på sista siffran först etc.)
– Olikheten mellan aritmetiska och geometriska medelvärdet och några relaterade olikheter (t.ex. a+1/a>=2 för positiva a). De flesta olikheterna går ut på att man ska få ”nånting i kvadrat >= 0”.
– Sinussatsen och cosinussatsen.
– Pythagoras sats.
– Likformighet.
– Randvinkelsatsen.
– Inskrivna (cykliska) fyrhörningar.
– Hur man räknar ut arean för olika figurer.
– Eventuellt de tredimensionella kropparnas volym.
– Lådprincipen.
Det är allt jag kan tänka ut på rak arm. Har du några tips?
Logiskt tänkande med små barn: träff 1 och 2
Denna höst har jag börjat jobba på ett helt nytt sätt. Jag undervisar fem- och sexåringar i matte i ryska klubben ”Kolobok” i Stockholm! En gång i veckan träffar jag fyra grupper med barn mellan (en med femåringar, två med sexåringar och en med tioåringar) och håller ungefär 40 minuter långa lektioner med dem på ryska (lektionerna ska delvis stimulera hemspråksinlärning).
Egentligen kallas våra lektioner för ”logiskt tänkande” och de flesta skulle inte kalla det vi gör för ”matte”. Men uppgifterna och aktiviteterna jag hittar kommer direkt från pedagoger som kallat sin verksamhet för ”matte för barn”.
Jag måste erkänna att jag aldrig har varit lärare för så pass små barn förut. Att hålla 7 stycken sexåringars intresse för en uppgift samtidigt är inte det lättaste som finns. Lägg på lite språkbarriärer då vissa av barnen inte förstår så mycket ryska. Recept för katastrof, eller? Helt illa har det ändå inte gått och jag vill gärna dela med mig om vilka aktiviteter som har funkat och vilka inte har funkat för barnen och varför.
Så vad har vi gjort på träffarna? Nedan kommer de viktigaste aktiviteterna jag genomförde för de minsta barnen under mina första två träffar med dem.
Barn och grafer
”Barn och grafer” är en bok av Frédérique Papy och Georges Papy som jag hoppas skulle passa mina småttingar. Den handlar om förskolelektioner som genomfördes i Frankrike. Lektionerna gick ut på att barnen skulle bekanta sig med olika sätt att representera objekt och reationer mellan dem (punkter och pilar), ett sätt att rita det hela på är med hjälp av grafer. Jag kommer ihåg att jag själv tyckte om boken som liten, men inte riktigt hur gammal jag var när jag kunde förstå det boken hadlade om.
Hur som helst tänkte jag testa att ha samma sorts lektioner med mina barngrupper. Första lektionen började med att vi pratade om syskon. Jag frågade barnen ifall de hade syskon och hur gamla syskonen var och det hade de flesta av barnen inga problem att svara på. Ett av barnen hade en bror som var 70 år tror jag :)
Sedan lade jag fram en stor bild med punkter och sa att punkterna var barn. Några av barnen hade inga problem med att räkna till femton. Men när jag sedan frågade vilka av barnen var flickor och vilka var pojkar istället för skratt (som det stod i min referenslitteratur) fick jag seriösa förslag på vilken punkt som var vem och av vilket kön.
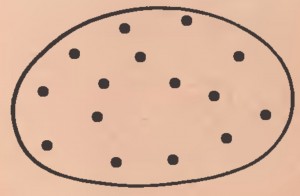
När jag frågade hur man skulle rita att varje barn pekade på sin syster var det bara i en grupp som ett av barnen föreslog pil som notation. Vi ritade lite pilar (många barn kunde rita hyfsade pilar, men inte alla), men bilden jag visade efter gav verkligen inte väntade resultat.
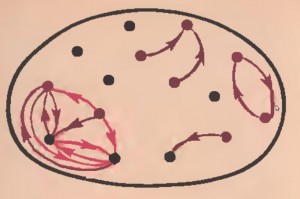
När jag nu frågade vilka barn som var flickor och vilka var pojkar fick jag svar på grund av frägen på punkterna och pilarna verkade ignoreras. Mina förklaringar om hur det egentligen låg till gav inga resultat så jag lade ner projektet. Det var nog alldeles för tidigt för dem att hålla på med grafer och därför inte så kul.
De märkte för övrigt att jag hade kvar muspekaren på en utskriven bild och undrade vad den gjorde där. Kanske är det en bra idé att ha stora bilder som man lägger fram och som alla barnen får peka på och rita i, men just de här uppgifterna var inte passande. Jag lägger boken på hyllan och eventuellt tar fram den senare.
Läsa berättelse
En till ”mattebok” ur min tidiga barndom. De är en rysk bok som egentligen är en saga, som handlar om två vänner: Tomatik och Kubarik. Handlingen är ett spännande äventyr som egentligen passar för barn mellan 3 och 6 år, men boekn är också väldigt pedagogisk. Allt eftersom introducerar begrepp som ”många”, ”ingen”, ”längd”, ”jämförelse” och så vidare som en naturlig del av berättelsen. För de flesta sexåringar är inga av begreppen nya, men just för mina kan det vara bra att de lär sig alla dessa ord på ryska.
När jag läste var det dock svårt att se vilka barn som lyssnade och vilka som tänkte på annat. Under olika träffar har jag försökt göra läsningen mer interaktivt och pekat i boken och ställt frågor, vilka flera av barnen gärna svarar på och då tycker att läsningen blir roligare. Ändå har jag valt att bara fortsätta läsa berättelsen för min grupp med femåringar. De andra har inte saknat berättelsen (jag läste för dem bara första träffen). En av femåringarna hörde jag däremot säga ”Kubarik är rolig” trots att det knappt har hänt nånting i boken hittills. Vännerna har städat och ritat och jämfört vem som haft längst tåg och längst järnväg. Kubarik är för övrigt en häst som Tomatik har byggt av kuber för att han ville ha en kompis.
Färgkoden
I somras köpte jag ett par pussel från Smart Games. Ett av dem heter ”Color code” och går ut på att man ska lösa pussel genom att kombinera olika färgbrickor (brickorna ska läggas på varandra och ovanifrån ska det se ut som på en bild i boken.) Det bästa är att det finns 4 svårghetsnivåer, så de flesta människor, inte vara barn, kan hitta en uppgift som är lite utmanande för dem.
Alla barnen ville göra en uppgift åtminstone en gång, vissa tänkte snabbt och ville verkligen hjälpa de andra. Några av barnen tvärtom sabbade för andra och gömde bitar. Allt som allt var det en lyckad aktivitet som vi återvände till när vi hade gått igenom allt planerat. Alla klarade av de problemen de fick. Jag hade med spelet både första och andra träffen.
Gissa och räkna antalet steg från en vägg till en annan (genomfördes bara med sexåringar)
Precis som det låter, det kändes som att barnen behövde röra på sig, så jag hittade på aktiviteten på plats (egentligen läste jag om någon som har genomfört denna aktivitet och att det har varit lyckat). Barnen tyckte att det var väldigt kul att gå från ena väggen till andra och räkna samtidigt. När jag gick med väldigt stoora steg och fick totalt få steg, förstod de att det blir färre steg då man går stort. Men de kunde inte säga rätt på frågan om vem som har flest steg direkt, eftersom begreppen “större antal” och “större steg” blandades ihop. Kanske berodde det på språkbarriären. Sedan började barnen springa okontrollerat under uppgiften ibland, hitta fler väggar etc. För några tog räkningen slut vid ex. 10 steg, eftersom de helt enkelt inte hade lärt sig räkna till mer.
Pilar
Som sidospår på ”barn och grafer” (se ovan) bad jag dem att rita pilar. Några ville rita många, några ville inte rita någon pil alls (om de fick en dålig (gul) penna). Sedan pratade vi om klockor (visare heter precis som pilar på ryska) och jag bad dem rita klockor. De flesta gjorde bra imitationer och kunde säga hur många visare deras klockor hade, men väldigt många gjorde spegelvända siffror av någon anledning. Det förvånade mig att det var fler som ritade spegelvända än rättvända siffror. Beror det på att de titta på klockan i spegeln eller är det bara en slump? Ofta skriver ju barn bokstäver spegelvänt till exempel.
Vi pratade sedan lite om klockor i allmänhet. Barnen kunde berätta om vad för form deras klockor hade (kvadrat, cirkel och till och med hjärta). Jag bad dem att göra läxa: titta på klockan hemma och rita av den så bra som möjligt. Bara ett barn tog med sig en ritning nästa gång, och då hade bilden alla möjliga klockor på sig. Det var nästan alla de hade hemma, vilket var typ 10 stycken! Kanske ska jag vara mer tydlig med läxan och ge den skriftligt (eller en helt en bild som de ska göra något med, det viktigaste är att de fysiskt får läxan och inte bara verbalt.)
Klockor
Till andra träffen tillverkade jag en klocka med bara timvisaren. Jag ställde in den på olika siffror och frågade varje barn en egen fråga ”vad är klockan?”. Alla kunde svara rätt. När jag sedan ställde in visaren precis mellan 6 och 7 blev det svårare. I en av gruppen tyckte någon att klockan var då 7, men när jag berättade för dem att det var snarare ”6 och lite till” kunde de svara på liknande frågor själva. Det här momenten kräver nogrann förklaring och tålamod när diskussionen sker. Väldigt synd för övrigt att vi inte kan ha så stora disskussioner eftersom många av barnen känner sig osäkra på språket.
Så småningom ska jag introducera minutvisaren, men det är nog för tidigt än. Först borde nog alla barnen lära sig att räkna till tolv.
Minisudoku
Alla barn fick var sin uppgift där de skulle fylla i en figur som saknas. Sådana här uppgifter brukar förekomma på IQ-tester, men egentligen är det bara en minisudoku med 3 siffror (3 sorts objekt). Bäst gick det i sexåringsgruppen där jag tog mig tid att förklara vad mönstret gick ut på. Jag hade färre deltagare då och kunde ha en diskussion om varför de ville rita en eller annan figur. Många föreslog fel figur fler gånger.
Några av barnen fick en liknande uppgift till och sedan en uppgift där 4 figurer av 9 saknades och man skulle komplettera mönstret. Alla de här uppgifterna var intressant nog mycket svårare för femåringar än för sexåringar. De som klarade uppgifterna fort och så att säga ”förstod mönstret” var lite besserwissers mot andra och sade att uppgiften var ”lätt”. Ett av barnen tyckte att det var en stjärna som saknades i rutan och ville absolut rita en varpå ett annat barn började rita ett eget mönster från en tom lapp med stjärnor, ovaler och rektanglar istället för de vanliga figurerna. Tyvärr blev det ett fel i det mönstret.
Mosaik
En stor del av andra träffen gick ut på att bygga bilder med mosaik. Jag har ett stort förråd med bitar som tar upp en halv ruta (trianglar), en ruta (cirklar och kvadrater) och två rutor (rektanglar) i olika färger som man kan fästa vid en platta och få till någon snygg bild eller mönster.
Uppgiften jag gav till de två första grupperna var att i par bygga två likadana figurer. Tanken var att de skulle hitta på något mönster tillsammans, men då de överhuvudtaget gick med på den här ”tävlingen” var det så att ena barnet dominerade och det andra försökte kopiera. I den sista gruppen gav jag istället uppgiften att bygga en symmetrisk bild (spegelsymmetrisk), vilket de flesta klarade någorlunda. Några barn försvann i sin egen värld och byggde helt enkelt det de ville bygga. Jag märker att många av barnen tycker om att rita och bygga med mosaik så det måste vi göra mer.
I överlag så tror jag att aktiviteterna har varit uppskattade, men jag behöver hitta på fler inför varje lektion, då barnen kan tröttna ganska snabbt eller rentav rata en aktivitet direkt. Fler kreativa uppgifter behövs och fler uppgifter då barnen ska röra på sig fysiskt.
Har du tips eller synpunkter, kommentera gärna. Jag försöker inte lära ut något specifikt förutom logiskt tänkande och resonerande egentligen, så alla sorts aktiviteter är välkomna!
Sista dagen för att anmäla dig till matematik-SM!
Nu är det snart igång igen! Sverige väljer sina skarpaste hjärnor bland gymnsieeleverna för att i sommar skicka de 6 bästa till matematik-VM eller IMO, som det egentligen heter. Jag blev imponerad av de senaste resultaten, då Sverige tog hem en silvermedalj! Det händer inte så ofta tyvärr.
Sista anmälningsdagen är 14 september. Jag har för mig att även högstadieelever kan få lov och delta. Jag skulle tro att mattebloggens läsare absolut har en chans att lösa ett par problem (av sex stycken). Dock kräver några av problemen ofta kunskaper som man får i tvåan eller trean på gymnasiet, så tävlingen är mer riktad på de sistnämnda. Men jag tycker att man ska känna på tävlingen även om man är yngre.
Här är lite info från den officiella hemsidan:
Den 27 september tävlar gymnasieskolor runt om i landet i Skolornas matematiktävling (även kallat matematik-SM). Tävlingen har arrangerats av den ideella föreningen Svenska matematikersamfundet sedan 1961 och firar i år 50 årsjubileum. Det är den äldsta tävlingen i matematik och naturvetenskapliga ämnen för gymnasieskolan. Förra året deltog 126 skolor runt om i landet i tävlingen.
Skolornas matematiktävling är ett av flera kvalificerande moment till deltagande i den ansedda Internationella matematikolympiaden (IMO). I juli i år arrangerades IMO 52:a gången 12-24 juli i Amsterdam. Sverige kom på plats 54 av 101 deltagande länder, en klar förbättring mot i fjol då Sverige hamnade på plats 72. Nästa matematikolympiad arrangeras i Argentina i juli 2012.
Uppdatering: Tips om vad man kan ”plugga på” innan tävlingen.
A Mathematician’s Lament och allt som är fel med matematikundervisningen i skolan
Det är inte eleverna som är dålig och inte heller är det lärarnas fel att ”matematiken” inte går in i elevernas hjärnor. Titta istället på kursplanerna för dagens mattekurser och försök att motivera varför vi på 2000-talet ska lära ut andragradsekvationer till samtliga gymnasieelever. Om du använder dig av matte i ditt liv försök att svara ärligt på hur mycket studierna egentligen har förberett dig.
A musician wakes from a terrible nightmare. In his dream he finds himself in a society where
music education has been made mandatory. “We are helping our students become more
competitive in an increasingly sound-filled world.”
Citatet ovan är från texten A Mathematician’s Lament, skriven av Paul Lockhart redan 2002. Jag läste den för bara ett par veckor sedan och den var fortfarande högaktuell och kommer vara det ett långt tag framöver! Jag har hittat texten som jag kommer utgå från när jag förbereder matematiklektioner i framtiden. Läs den! Du kanske håller med eller tycker att den är helt överdriven, men förhoppningsvis kommer den leda dig till nya tankar om matematikundervisningen i Sverige.
Problem om att ta sig över till andra sidan
Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett problem kunde inte de flesta deltagarna lösa:
En familj kommer fram till en bro mitt i natten. Pappan kan gå över bron på 1 minut, mamman – på 2 minuter, barnet – på 5 minuter och mormorn – på 10 minuter. De har bara en lykta. Bron håller bara för två personer åt gången. Hur ska alla ta sig över till andra sidan på 17 minuter? (Om två personer går över samtidigt, går båda lika snabbt som den långsammaste av dem. Man får inte gå på bron utan lyktan. Man får inte lysa långt bortifrån. De får inte bära varandra.)
Ännu tidigare i min matematiska karriär hörde jag talas om problemet om Bonden och hans ägodelar:
En man ska ta sig över en å i en roddbåt. Han medför en varg, en get och ett kålhuvud. Han kan inte ta med sig mer än en av ägodelarna åt gången. Vargen kan inte lämnas ensam med geten och geten kan inte lämnas ensam med kålhuvudet. Hur skall mannen bära sig åt för att klara övergången?
Kanske vet du lösningen, kanske inte. Det är roliga är att numera finns problemet i form av ett spel!
Prova även att få över missionärer och kannibalen till andra sidan. Båten rymmer två, men blir det fler kannibaler än missionärer på någon sida, blir missionärerna uppätna.
Och till slut kan du prova att få över familjen med lyktan på andra sidan. Den här familjen är dock lite större än i problemet i början, och har lite annorlunda tider. Men illustrationen till problemet är suverän.
Alla ni som tyckte om problemen om familjerna, kan försöka lösa det generella fallet. Vilket är den minsta tiden att ta alla över till andra sidan, om familjen har 
