Roligare matematik
Grattis på Pi-dagen!
Talet pi är förstås relaterat till cirklarnas area och radie, men följande uppgift kan du lösa utan att kunna några formler.
Vilken kvadrat har störst orange area?
(Även om du kan använda dig av formler, prova att lösa uppgiften utan dem!)
Uppgiften och bilden är från donsteward.blogspot.com
Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.
Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i förhållande till koordinatsystemet, eftersom mittpunkten ligger i vårt fall antingen i en heltalsnod eller i mitten av en ruta). Men kan vi hitta en cirkel med ett annat antal punkter på periferin, t.ex. 6?
Vi vill alltså ta reda på för vilka n det går att hitta en cirkel som går igenom exakt n heltalspunkter.
Går det att hitta en cirkel med en heltalsnod på periferin? Så klart går det, vi kan t.ex. ta en cirkel med en väldigt liten radie som går igenom en godtycklig punkt.
Två heltalsnoder på periferin då? Ja, vi kan ju skapa cirklar som inte är rotationssymmetriska, men däremot spegelsymmetriska, genom att välja att ha mittpunkten på cirkeln i (0, 0.5) till exempel eller egentligen var som helst mellan två närliggande heltalsnoder. Tar vi radien lika med 0.5 så är vi garanterade att inga andra heltalsnoder än (0,0) och (0,1) kommer med på cirkelns periferi.
Hur gör vi med 3 punkter på periferin? Cirkeln får nu varken vara spegelsymmetrisk eller rotationssymmetrisk med avseende på heltalsnoderna (om två periferipunkter ligger strikt på vänstra/högra halvan av cirkeln). Således måste vi placera mittpunkten varken i en heltalspunkt eller i en ”halvtalspunkt”. Under några antaganden kan vi försöka hitta en cirkel med två heltalspunkter som befinner sig på samma vertikala linje. Vi antar att cirkelns horisontella diameter ligger på linjen y=0.
Koordinaterna för mittpunkten är då (s, 0) och för heltalsperiferipunkterna (0, a), (0, -a) samt (b, 0). Då får vi likhet av två radier (i kvadrat):
s2 + a2 = (b – s)2
s2 + a2 = b2 – 2bs + s2
a2 = b2 – 2bs
Både a och b är positiva heltal, medan s är ett positivt reellt tal (förmodligen större än 1). Därför måste b vara åtminstone 3 och vi prövar b = 3.
Då måste a2 = 9 – 6s. Tar vi a = 1 får vi s = 4/3 vilket ger oss cirkeln:
Denna har exakt 3 punkter på periferin! Men hur gör man i det allmänna fallet? Kan man alltid få relativt snygga cirklar, det vill säga där punkterna ligger i par på respektive vertikallinjer? Det visar sig att man kan det med hjälp av Schinzels sats!
Det existerar en cirkel med exakt n heltalspunkter på periferin för varje naturligt tal n.
För jämna n=2k har Schinzels cirkel ekvationen
Medan för udda n=2k+1 har Schinzels cirkel ekvationen
Testa till exempel hur cirkeln med exakt 7 heltalspunkter på periferin ser ut!
Schinzels cirklar är inte nödvändigtvis de minsta med den egenskapen, men de är i alla fall snygga på sättet beskrivet innan, nämligen att heltalspunkterna på periferin förekommer i par, vilket kan ses från ekvationen (mittpunkten ligger på en horisontell heltalslinje).
Kan du bevisa att Schinzels cirklar uppfyller egenskaperna som det påstås i satsen? Helt trivialt är det ju inte att bevisa.
Tack Sture Sjöstedt för frågeformuleringen, samt länkar och tips!
I föregående del avslöjade vi processen med vilken vi kan förstora koordinatsystem på så sätt att de förstorade ciklarna innehåller icke-primitiva pythagoreiska tripplar.
Om ett heltal kan representeras som en summa av två kvadrater, så kan vi alltid förstora primitiva pythagoreiska tripplar med detta heltal. Till exempel är 5 = 1+4 = 12+22, alltså en summa av två kvadrattal. Rita då nya rutor (gå 1 steg åt ett håll och 2 åt ett annat) i det gamla koordinatsystemet, rutorna kommer ha area 5. Det betyder att alla areor kommer vara exakt 5 gånger större!
Hur är det med andra förstoringen av primitiva pythagoreiska tripplar, till exempel med faktor 3? Låt oss bevisa att trippeln (9,12,15) inte kan uttryckas i form av rektangelareor på en och samma cirkel. Specifikt undersöker vi hur rektangeln med arean 9 kan se ut.
Givetvis kan det vara en vanlig 3×3 eller 1×9 rektangel, där sidorna går längs med rutnätslinjerna. Men kan en rektangel med arean 9 ligga snett i rutsystemet?
Om en rektangelns ena sida ligger snett, så kommer rutnätspunkterna finnas på den med jämna mellanrum. Låt mellanrummets längd vara a. Vinkelrätt mot första sidan går rektangelns andra sida. Där hamnar rutnätspunkterna med exakt samma mellanrum. Eftersom rektangeln har sina hörn i rutnätspunkter, kommer alltså ena sidan består av k antal a:n och andra sidan av m antal a:n. Det vill säga k och m är heltal, medan a är roten ur summan av två heltalskvadrater.
Så arean på en sådan sned rektangel är k*m*a2, alltså en produkt av heltal. Det betyder att om k*m*a2=9, så är a2=1, 3 eller 9. Men varken 1, 3 eller 9 kan skrivas som summa av två positiva heltalskvadrater. Därför finns det inga sneda rektanglar med arean 9.
Överlag måste alltså någon av areans delare kunna uttryckas som en summa av två positiva kvadrattal, för att det ska finnas en sned rektangel med denna area. Det är dessutom ett tillräckligt villkor.
Det betyder att endast två rektanglar har area 9. Rektanglarnas mittpunkt sammanfaller med den omskrivna cirkelns, vi har alltså två varianter.
Men den första cirkeln innehåller bara en enda rektangel, medan den andra innehåller den primitiva pythagoreiska trippeln (9, 40, 41) och inga andra rektangelareor. Så trippeln (9,12,15) går inte att konstruera på det här sättet!
Så vi har hittat minst en trippel som inte är konstruerbar på det här sättet. Jag vet fortfarande inte om det är så att alla icke-primitiva tripplar med en faktor, som inte är en summa av två kvadrater, är okonstruerbara. Kanske kan du hitta ett motexempel?
Men denna fortfarande öppna fråga avslutar vi den här serien inlägg om pythagoreiska tripplar i form av areor. Läs gärna serien från början, kanske upptäcker du nya idéer när du läser för andra gången!
I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).
Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
Nej, det kan dyka upp fler än så, vilket beror på att vi kan hitta cirklar där fler än 8 rutnätspunkter hamnar på cirkeln. Nedan ser ni nio olika rektanglar, med areor utskrivna, som vi kan hitta i en cirkel med 16 rutnätspunkter på randen. (Vad tror du förresten är det största antalet rutnätskpunkter man kan hitta på en cirkel?)
Men hur gör man med icke-primitiva Pythagoreiska tripplar? Konstruktionen från förra delen fungerar inte, eftersom icke-primitiva tripplar kan inte genereras på samma sätt från m och n som primitiva.
En icke-primitiv trippel är däremot lika med en primitiv, multiplicerad med en faktor, som till exempel (6,8,10) är trippeln (3,4,5) multiplicerad med faktorn 2. Om vi på något sätt kunde förstora alla rektanlar med faktorn 2, utan att förlora rutnätsegenskaperna, så skulle problemet vara löst. Men förstorlingen av alla rektanglar med faktorn 2 skulle ske om alla sidor förstorades med faktorn √2.
Detta kan vi göra om vi helt enkelt förstorar hela rutnätet med faktorn √2! Vi gör det genom att rotera koordinataxlarna 45 grader och betrakta fyra punkter som bildar en kvadrat med sidan √2 som en enda ruta. På bilden nedan är det nya rutnätet ritat i rött ovanpå det gamla (eftersom vi trots allt använder det gamla för att rita ut cirklar).
Vi gör samma sak med rutnätscirkeln: rotera och förstora med faktor √2, då bildar från en cirkel med areorna (3,4,5) en annan cirkel med rektangelareorna (6,8,10). Punkterna på cirkeln numreras för det ska gå lättare att se rotationen.
Men såklart kan vi bilda nya rutsystem på andra sätt och med andra rutstorlekar! Bland annat går att att förstora alla areor med 5, med 13 och såklart med produkter av faktorer, som vi redan kan förstora med. (Försök att hitta ett rutsystem med rutlängderna √5). På så vis går det alltså att konstruera alla icke-primitiva taltripplar på formen t.ex. (5*(m2-n2),5*2*m*n,5*(m
Men går att förstora på så sätt med alla faktorer? Går det till exempel att konstruera den icke-primitiva trippeln (9,12,15)? Vi besvarar den här frågan i den sista delen.
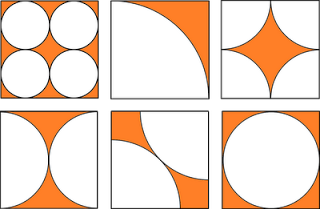
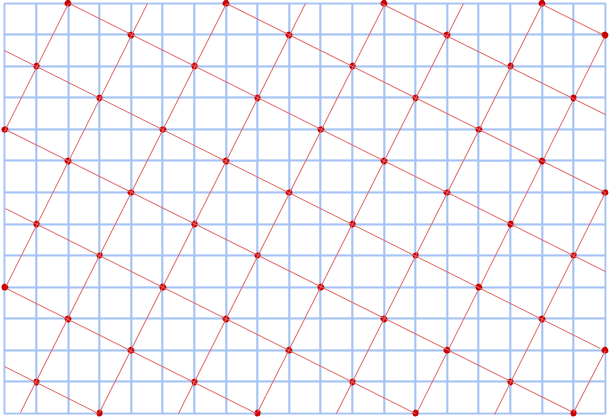
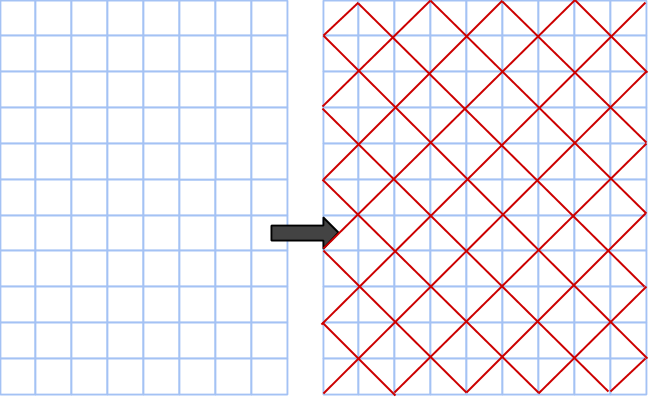
I del 1 såg vi hur vissa pythagoreiska tripplar kunde representeras i form av areor på rektanglar inuti cirklar på rutnät. I den här delen undersöker vi huruvida detta är möjligt för alla primitiva tripplar.
Primitiva pythagoreiska tripplar (a,b,c) är sådana att talen a, b och c inte har några gemensamma delare. Till exempel är (3,4,5) en primitiv pythagoreisk taltrippel, medan (6,8,10) är en icke-primitiv sådan.
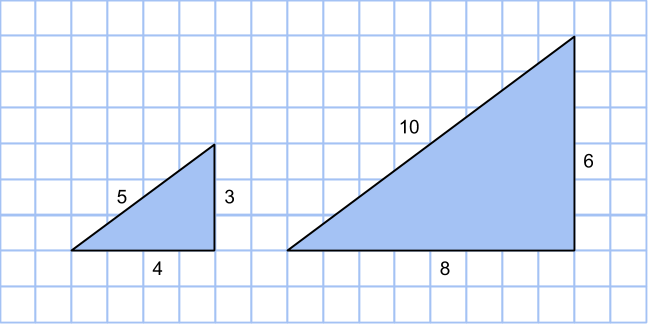
Ur varje icke-primitiv pythagoreisk taltrippel kan vi nämligen få en primitiv: Om de tre talen har största gemensamma delaren d, så kan de skrivas på följande sätt: a = d·r, b = d·s och c = d·t.
Eftersom a2 + b2 = c2, så är även (dr)2 + (ds)2 = (dt)2. Förkortar vi likheten med d2, så får vi r2 + s2 = t2. Således har vi fått en ny pythagoriesk trippel (r,s,t). Den är primitiv, eftersom r, s och t inte kan ha några gemensamma delare (deras gemensamma primfaktorer skulle ha ingått i d).
Ur primitiva taltripplar kan man förstår tvärtom få oändligt många icke-primitiva genom att multiplicera alla tre talen med en och samma faktor.
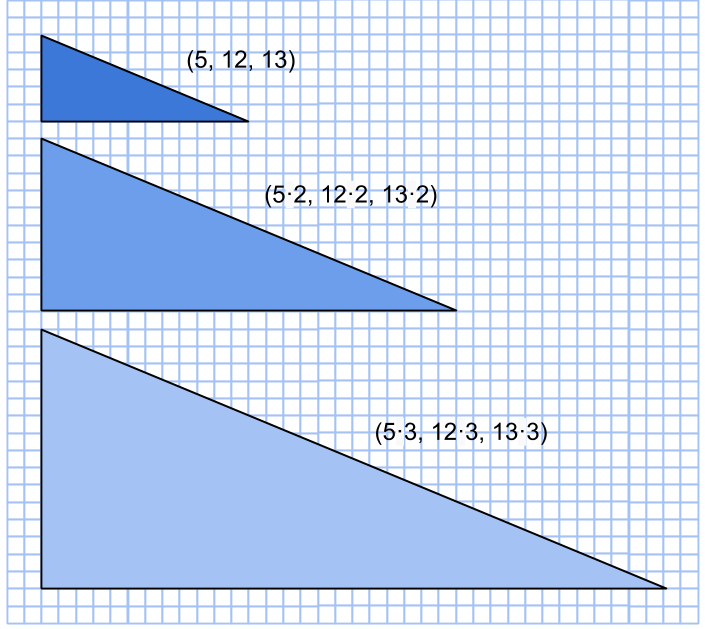
Således finns det oändligt många pythagoreiska taltripplar, men finns det oändligt många primitiva?
Ja, det visar sig att det finns oändligt många sådana och dessutom genereras varje primitiv trippel genom två heltal, som vanligen betecknas m och n. Dessa tal bör vara relativt prima och ett av dem måste vara udda, medan det andra måste vara jämnt. Givet sådana två tal, kommer följande tre tal bilda en pythagoreisk trippel: (m2-n2, 2mn, m2+n2). Kontrollera gärna att oavsett vad m och n är, så kommer Pythagoras likhet gälla för dem.
Till exempel kan trippeln (3,4,5) skrivas som (22-12, 2·2·1, 22+12), det vill säga den genereras av talen 1 och 2.
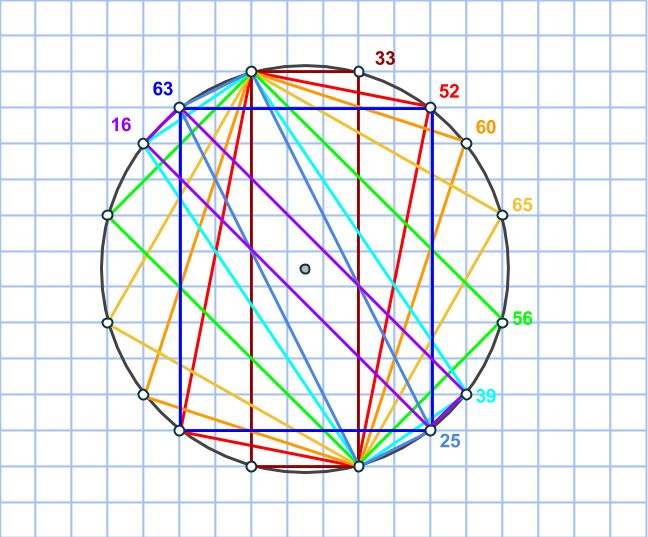
Talen 3 och 8 ger oss trippeln (2·3·8, 82-32, 82+32), det vill säga (48, 55, 73) och just för det exemplet kommer vi rita upp en cirkel som innehåller rektanglar med respektive areor. Men låt oss beskriva hur vi agerar för allmänna m och n, det vill säga för en godtycklig primitiv pythagoreisk taltrippel.
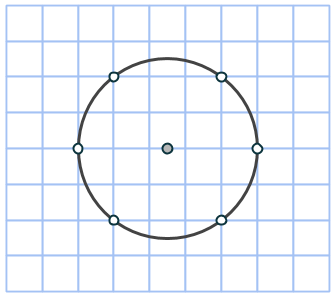
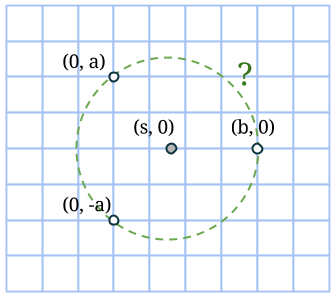
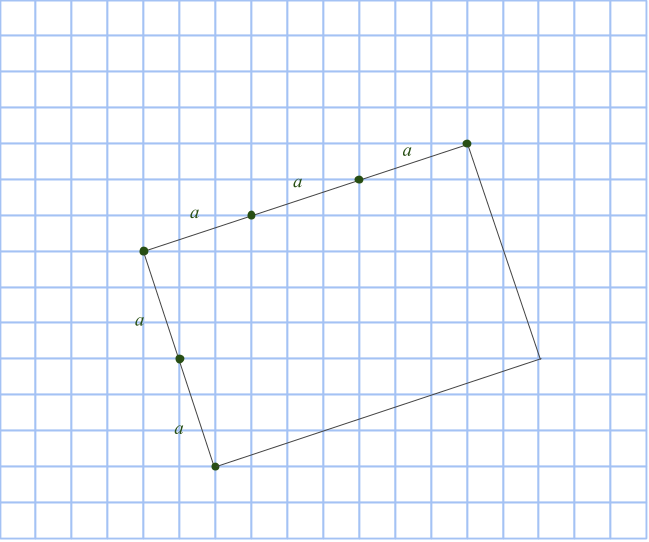
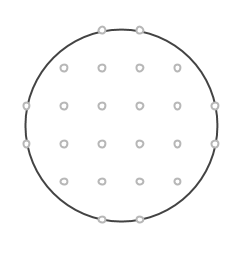
Talen m och n är nämligen till stor hjälp när cirkeln konstrueras. Vi börjar inte i cirkelns mittpunkt, som man skulle kunna tro, utan på en punkt på randen (en heltalspunkt, som kommer vara hörn för åtminstone en rektangel). Markera en punkt m+n steg nedanför startpunkten, samt m-n steg till höger. Komplettera till en rektangel med en fjärde punkt på rutnätet. Rektangelns area är (m+n)(m-n) = m2 – n2 och dess mittpunkt måste sammanfalla med cirkelns. Vi bestämmer den genom att korsa diagonalerna.
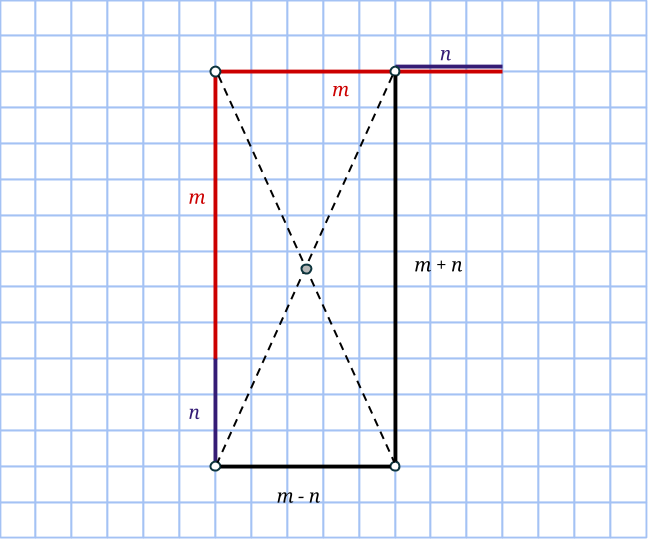
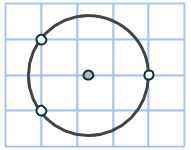
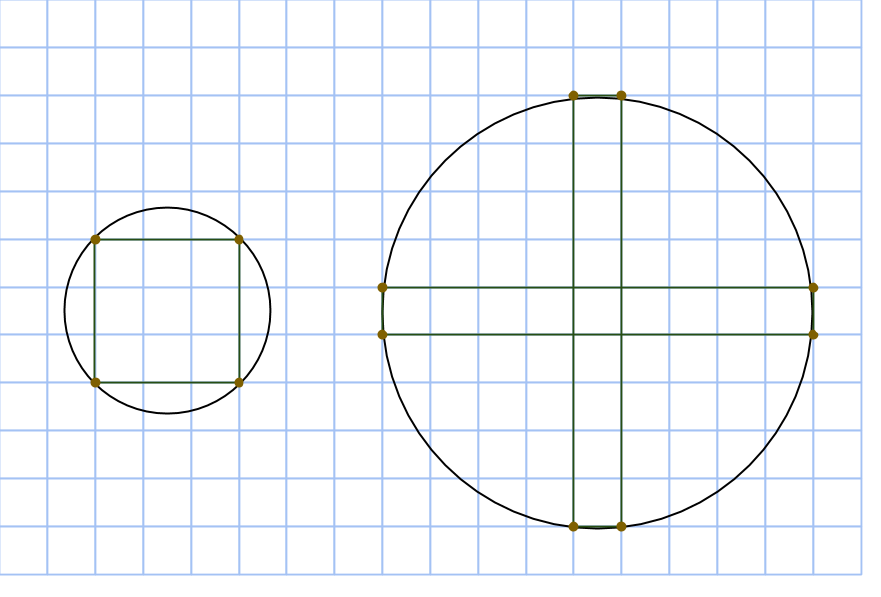
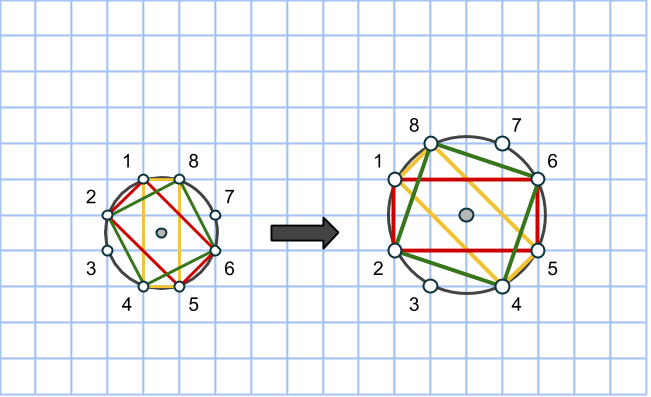
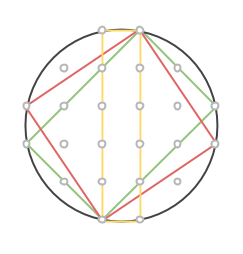
Rektangeln vi har ritat är uppenbarligen inte en kvadrat, så vi får fyra nya rutnätspunkter som också ligger på cirkeln genom att rotera rektangeln 90 grader runt cirkelns mittpunkt:
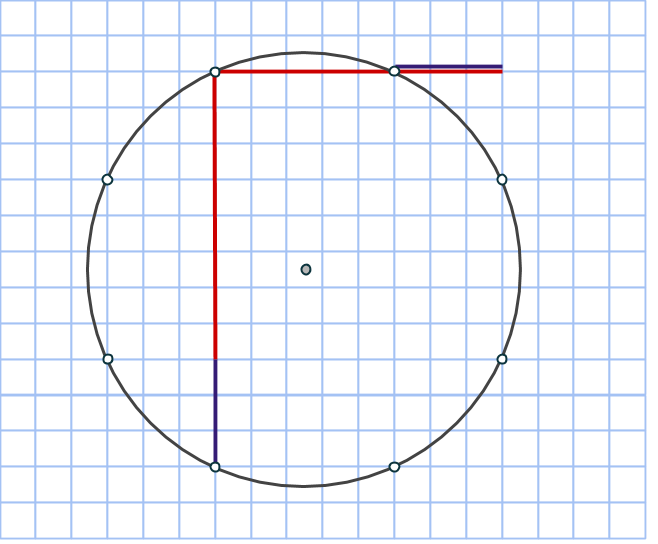
Nu har vi fått en cirkel med åtta rutnätspunkter utsatta och det är faktiskt allt vi behöver! Låt oss bevisa det.
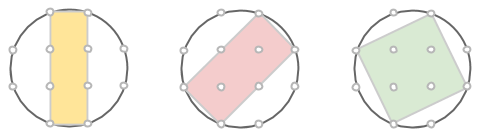
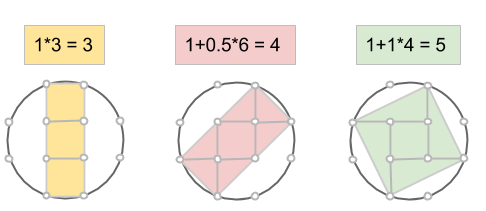
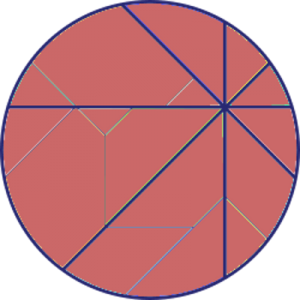
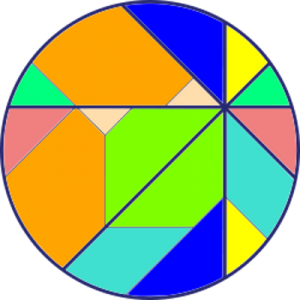
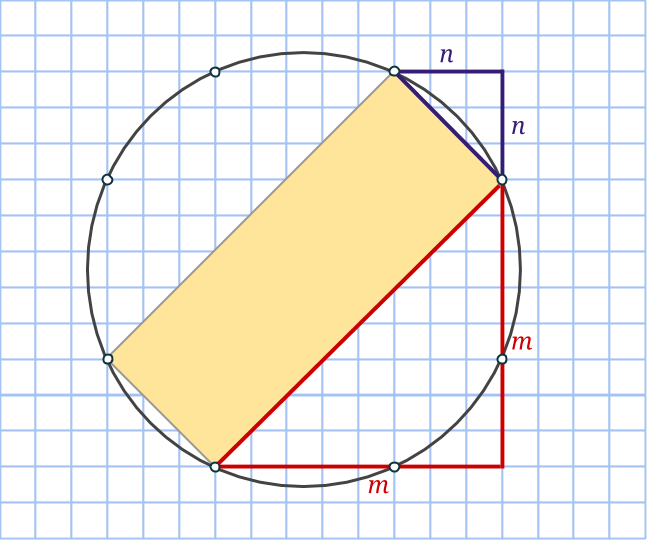
Markera en rektangel som har sina sidor vinklade 45 grader i jämförelse med den första. Kortsidan utgör hypotenusan i en likbent rätvinklig triangel med sida n, medan långsidan är på samma sätt, fast med m. Då kommer alltså arean att vara √(2n2)·√(2m2) = √(4m2n2) = 2mn. Precis som ett av talen i den pythagoreiska trippeln.
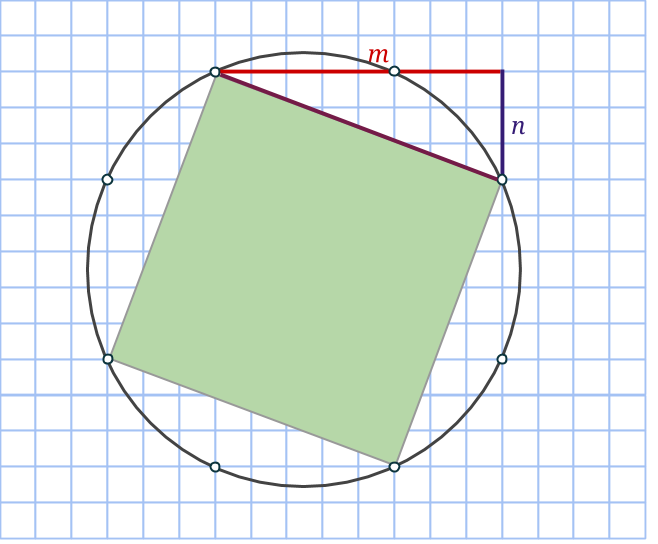
Markera nu en rektangel, som dessutom är en kvadrat genom att ta varannan punkt på cirkeln. Sidan blir lika med √(m2+n2), så arean måste bli lika med just m2+n2. Därmed är den sista arean funnen!
Nu uppstår det fler frågor: Dyker det någonsin upp några extra rektanglar med en annan area vid en sådan konstruktion? Och hur gör man för att konstruera cirklar för icke-primitiva pythagoreiska taltripplar?
Vi försöker besvara dessa frågor i nästa del.
[kkratings]
Föreställ dig ett rutnät av punkter. Det går att hitta massvis med cirklar som går igenom några av punkterna. En av de minsta sådana cirklarna har hela 8 punkter på sin rand:
Det går även att hitta några rektanglar inuti sådana cirklar, som har alla sina hörn i punkterna på cirkelns rand (notera att även kvadraten räknas som en rektangel). Kan du bestämma rektanglarnas areor?
Kan du på samma sätt i cirkeln nedan hitta rektanglar med areorna 5, 12 och 13?
Följande fråga uppstår: går det att hitta vilken Pythagoreisk trippel som helst på samma sätt?
Geometri är inte bara någonting skäggiga greker höll på med, utan den kan vara användbar även för den gemene svensken – till exempel när man ska dela en rund pizza!
Om man får en pizza hemkörd och ska dela den på två personer, så brukar man skära pizzan i två halvor. Problemet är att om man inte skär precis genom mitten, så kommer inte halvorna att bli lika stora.
En metod som garanterar rättvis fördelning av pizzan är följande. Välj en punkt inuti pizzan, vilken som helst, och gör fyra snitt, med 
Då, om ena personen får varannan utav bitarna som bildas, medan den andra får resten, så kommer båda få exakt hälften utav pizzan.
Den generaliserade versionen av pizzasatsen, där man kan dela pizzan i ännu fler delar med lika stor vinkel mellan snitten (12, 16 delar osv.), bevisades av L.J.Upton 1968.
Man kan bevisa satsen på olika sätt, men bland annat finns ett bevis som består av en enda bild.
Nyfiken på beviset? Se ledtrådarna nedan i så fall.
Grattis på pidagen!
[kkratings]
Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer han 30 km. Visa att summan av alla vinklar, som lejonet svängde under springturen, är minst 2998 radianer.
Källa: Kvant magazine
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft en introduktion till vinklar och olika vinkeltyper.
Var hittar vi vinklar i rummet? Det är svårt att hitta spetsiga och trubbiga vinklar, men klockans visare bildar oftast en spetsig eller trubbig vinkel. Vi tar fram en modell av en klocka med två visare och snurrar ena visaren. Barnen säger under tiden vilken vinkel det är mellan visarna (”trubbig, trubbig, trubbig, trubbig, RÄT, spetsig, spetsig, spetsig, jättespetsig…”).
Vad är klockan om visarna bildar en rät vinkel (om minutvisaren är på tolv)? De yngre barnen får experimentera med en klockmodell, medan de äldre får föreställa själva. Hur ofta sammanfaller visarna, kan man fråga de äldre barnen.
Ställer man en spetsig vinkelns ena ben på marken blir det en backe. Vilken backe åker man snabbast nedför? Vilken backe är jobbigast att klättra upp på?
Tänk om vi har varken linjal, gradskiva eller sax med oss! Det enda vi har är ett papper. Hur kan vi få fram en rät vinkel? Vad ska vi göra om pappersbiten är rund och inte triangulär från början?
De äldre barnen får i uppgift att vika ihop vinklar på 180, 90, 45 samt 60 grader.
Vi ska göra den tråkiga klockan lite snygg och färglägga cirklarna med siffror. Går det att måla cirklarna i två färger, så att varannan cirkel har en färg? Kommer det att gå ihop på slutet? Går det med 3 färger? 4 färger? 5 färger?
Tio- och kanske sjuåringarna får hitta tal upp till 100 som går att färga i både 2,3,4,5 och 6-färgsmönster.
I samband med det får de kort där de snabbt ska gissa hur många cirklar det finns av en viss färg.
Till exempel, hur många röda cirklar är det på bilden? Svara utan att räkna dem en efter en!
Vi fortsätter på uppgiften från förra gången. Nu gäller det att inte bygga en cirkel utav vilka bitar som helst, utan av exakt två typer av bitar. Det finns inte så många lösningar till den här uppgiften om man lägger på begränsningar på att varannan bit ska ha samma färg (ett exempel är 
En ny termin är igång och för mig innebär det söndagsträffar med mina matematiksugna 5-, 6-, 7- och 10-åringar! Förra terminen skrev jag om våra 6 träffar, men vi har egentligen haft 11 stycken och i vår ska vi ha ungefär lika många!
Gamla träffar:
Träff 1 och 2
Träff 3 och 4
Träff 5 och 6
Den här våren tänkte jag prova att ha 1-2 övergripande teman på varje lektion, ungefär samma tema för stora som för små barn. Uppgifterna kommer dock variera för olika åldrar. De planerade aktiviteterna ska jag försöka lägga upp här på bloggen i förväg, så ni kan komma med synpunkter och förslag. De riktiga lektionerna blir aldrig i och för sig exakt som planerat, men i alla fall hälften av aktiviteterna hinns med (det gäller att ha aktiviteter med sig med marginal!).
Vi har nämnt vinklar och hörn lite grann förra terminen och svarat på frågor av typen:
– Hur många hörn har rummet? (Svaret var 6 för vårt rum)
– Hur många hörn har bordet? (Svar: 4)
– Bordet består egentligen av två mindre. Hur många hörn blir det om man förskjuter ena halvan? (Svar: 8, eftersom vinklar som är större än 
Här är en kortfattad plan på hur jag ska lägga upp lektionen för barnen (där det inte står något, utgå från att de är 5-7 år gamla):
Jag berättar om spetsiga, räta och trubbiga vinklar, visar exempel och ber dem att hitta olika sorts vinklar i rummet. Finns det andra vinklar än räta i verkligheten? Ja, men man får leta efter dem lite längre (ett exempel är klockans visare).
Barnen får dra kort, ett i taget, och säga vad för sorts vinkel det är på bilden (trubbig, spetsig, rät). Man måste visa att man har rätt också och det kan man göra genom att lägga vinkel inuti en rät t.ex., för att visa att den är spetsig. Sådant kommer jag be om, när en vinkel är väldigt nära en rät, så det är svårt att avgöra vinkelns sort. Jag frågar efteråt om det finns vinklar som är lika stora och även då får barnen bevisa sina hypoteser genom att t.ex. lägga vinklarna på varandra.
Bara den färgade delen (själva vinklarna) ska lamineras för att uppgiften ska gå att genomföra som planerat.
För att associera även det inre med ordet ”vinkel” (se bilden nedan), ska vi måla lite (barn älskar att måla!) och samtidigt träna lite kombinatorik.
Hur många vinklar ser du på bilden? Måla alla möjliga vinklar i olika färger (det finns 6 stycken mindre än 180 grader och barnen får 6 uppsättningar av bilden):
Barnen ritar några egna vinklar. Vissa får i uppgift att rita spetsiga, vissa trubbiga och vissa räta.
Nästa uppgift är att rita två linjer som skär varandra och räkna antalet spetsiga samt trubbiga vinklar på bilden.
Jag har med ett pusselspel, som egentligen är menat till att lära sig bråk. Det är cirkelsektorer i plast i olika färger som är lika stora som 1/3 av cirkeln eller 1/8 till exempel. Sektorer av samma storlek har samma färg, till exempel är alla tredjedelar gula, alla åttondedelar – gröna.
Plastbitarna presenterar jag som vinklar. Barnens uppgift är att bygga ihop en cirkel utan ”vinklar” som inte alla har samma färg. Till exempel, ![\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\](http://l.wordpress.com/latex.php?latex=%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B3%7D%2B%5Cfrac%7B1%7D%7B6%7D%5C%20&bg=FFFFFF&fg=000000&s=0 "\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\")
![\ 180^\circ+120^\circ+60^\circ=360^\circ\](http://l.wordpress.com/latex.php?latex=%5C%20180%5E%5Ccirc%2B120%5E%5Ccirc%2B60%5E%5Ccirc%3D360%5E%5Ccirc%5C%20&bg=FFFFFF&fg=000000&s=0 "\ 180^\circ+120^\circ+60^\circ=360^\circ\")
Dessa ”tårtbitar” återvänder vi till när vi ska prata om bråk.
De äldre barnen (10 år) får göra samma uppgift, men de måste mäta vinklarna med gradskiva och lägga ihop siffrorna, för att komma fram till att summan är 360 grader om vinklarna tillsammans bildar en cirkel.
Andra experiment för de äldre är att rita trianglar, riva bort hörnen och mäta vinkelsumman. Alternativt lägga hörnen bredvid varandra och se att det blir en rät linje (alltså 180 grader). Samma uppgift med fyrhörningar och femhörningar.
Jag visar för de äldre barnen hur man kan rita exakta vinklar med hjälp av en gradskiva. Sedan får de lära sig att rita en femuddig regelbunden stjärna med passare, linjal och gradskiva.
Detta är allt för den första lektionen om vinklar! Notera att jag också hade tänkt med att hinna med ett annat tema, nämligen tal upp till 100 (och med de äldre barnen, delbarhet upp till 100).
© 2009-2024 Mattebloggen
är sträckorna som lejonet springer på, medan 
är vinklarna som han svänger på. Betrakta lejonets bana på följande sätt.
med längden 
. Rotera då arenan kring lejonet, det vill säga punkten 
, med vinkeln 
, på så sätt att sträckan 
blir en fortsättning på sträckan 
, rotera arenan med vinkeln 
, så att 
utgör fortsättningen utav 
, som är 30000 meter lång.
rört sig under tiden? Först roterar 
med vinkeln 
vid första rotationen, 
mäts i radianer). Så 
. Alltså:
.
, slutarenan ger 
. 
, så är 
. Således har vi att:
radianer.