Klassiska bevis: Randvinkelsatsen

Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.

Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar och randvinklar. Annars läs vidare här.

Sats (Randvinkelsatsen)

Markera tre olika punkter A, B och C på en cirkel. Markera även cirkelns mittpunkt O. Då är vinkeln AOC dubblet så stor som vinkeln ABC.

Bevis

Man ska vara väldigt försiktig och rigorös med geometriska bevis. Med det menas att alla möjligheter för bildens utseende ska undersökas, om man nu ska rita någon bild överhuvudtaget.

Så till exempel, kan det se ut så här:

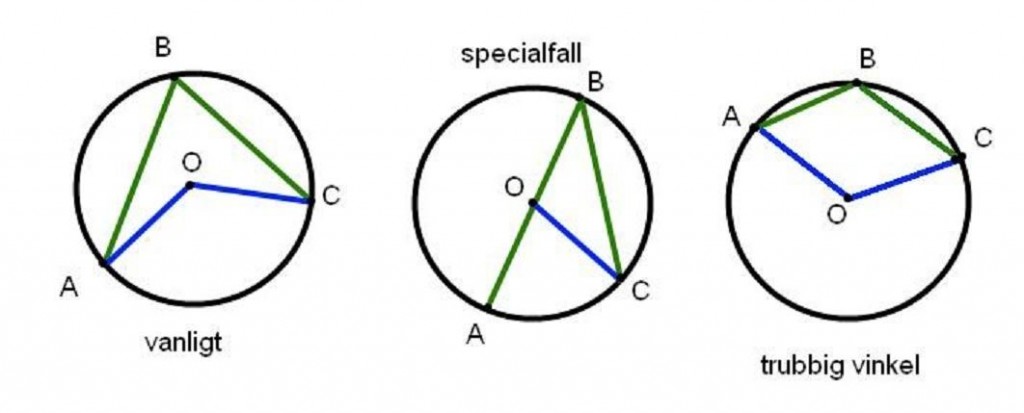Så hur ska man täcka alla möjligheterna på ett bra sätt? Det beror förstås på vad man tänker baser beviset på.

Oftast betraktas bilderna som väsentligen olika om olika skärningar mellan linjerna äger rum. I bevisen grundar vi ofta resonemang på hur olika objekt ligger i förhållande till varandra och inte så mycket på storlekarna på vinklar, cirkelbågarna etc.

Med detta sagt väljer vi således att betrakta tre fall (som täcker alla möjliga situationer):


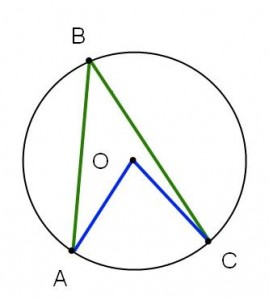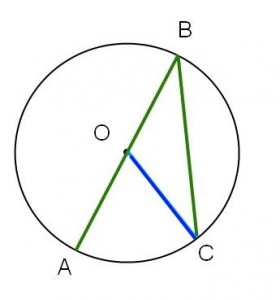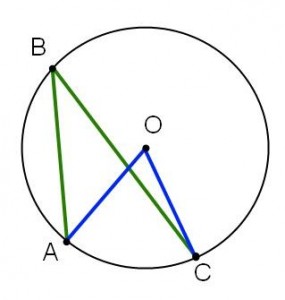Fall I	Fall II	Fall III

Fall I: Vinkel AOC ligger helt inuti vinkeln ABC.
Fall II: Detta är specialfallet då vinkeln AOC delar sida med vinkeln ABC.
Fall III: Två av vinklarnas sidor skär varandra.

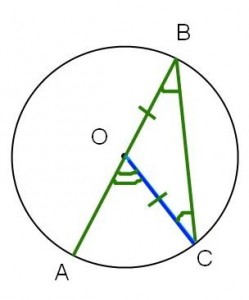
Fall II

Detta fall verkar vara enklast, så vi börjar med det. OB=BC för att de är radier, så $\triangle COB$ är likbent. Alltså gäller $\angle OBC = \angle OCB$ .

$\angle AOC + \angle BOC = 180\textdegree$ men också $\angle OBC + \angle OCB + \angle BOC = 180\textdegree$ .
Då måste $\angle AOC = \angle OBC + \angle OCB = 2\angle OBC$ . Vilket skulle bevisas.

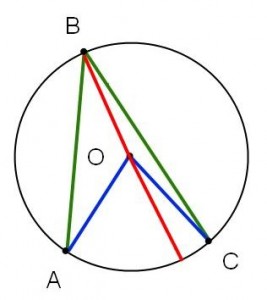
Fall I

Första fallet då? Vi ”fuskar lite” och drar en hjälplinje. Men nu får vi egentligen Fall II igen! Tillämpa det på varje halva av bilden och addera.

Fall III

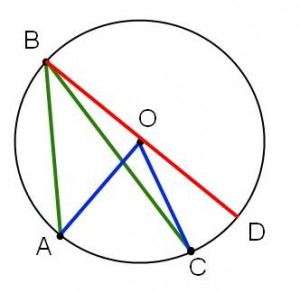Fall III måste väl vara svårare? Inte då! Vi ”fuskar” och drar en hjälplinje igen. Vi får återigen på grund av Fall II att $2\angle DBA=\angle DOA$ och att $2\angle DBC=\angle DOC$ . Subtrahera det andra resultatet från det första och vi är klara!

Relaterade

3 reaktioner till “Klassiska bevis: Randvinkelsatsen”

Hur sluter du dig till att endast dessa tre fall existerar, det vill säga att alla fall är specialfall av något av dessa?

Dessa tre fall är: punkten O ligger inuti vinkeln ABC, på eller utanför. Endast dessa villkor används i bevisen för respektive fall.

Vissa saker förblir obevisade, som till exempel att om vi i första fallet drar linjen BO så korsar den just den bågen AC som B inte ligger på. Sådana små bevis är inte så svåra, och framförallt intuitiva, därför utelämnar man dem oftast.

Ett praktexempel på att principen att något måste antingen vara mindre än, lika med eller större än något annat. Något genant att jag inte såg det.

Jag håller med dig om att man i viss utsträckning skall utelämna vissa små delar av bevis, främst på grund av att man i annat fall riskerar att förstöra en vacker idé med omotiverad formalism. Det kan då uppstår ett sådant scenario att man inte ser skogen på grund av att träden är i vägen. Självklart finns det dock fall då strikt formalism är nödvändig eller då det klargör beviset i stället för att förstöra det.

Denna webbplats använder Akismet för att minska skräppost. Lär dig hur din kommentardata bearbetas.

Toomas skriver:

27 december 2010 kl. 16:47

Hur sluter du dig till att endast dessa tre fall existerar, det vill säga att alla fall är specialfall av något av dessa?
Val skriver:

08 januari 2011 kl. 16:23

Dessa tre fall är: punkten O ligger inuti vinkeln ABC, på eller utanför. Endast dessa villkor används i bevisen för respektive fall.

Vissa saker förblir obevisade, som till exempel att om vi i första fallet drar linjen BO så korsar den just den bågen AC som B inte ligger på. Sådana små bevis är inte så svåra, och framförallt intuitiva, därför utelämnar man dem oftast.
Toomas skriver:

11 januari 2011 kl. 17:41

Ett praktexempel på att principen att något måste antingen vara mindre än, lika med eller större än något annat. Något genant att jag inte såg det.

Jag håller med dig om att man i viss utsträckning skall utelämna vissa små delar av bevis, främst på grund av att man i annat fall riskerar att förstöra en vacker idé med omotiverad formalism. Det kan då uppstår ett sådant scenario att man inte ser skogen på grund av att träden är i vägen. Självklart finns det dock fall då strikt formalism är nödvändig eller då det klargör beviset i stället för att förstöra det.