Två personer anländer oberoende av varandra till en bestämd plats mellan 9.30 och 10.00. De stannar på platsen i exakt tre minuter. Hur stor är sannolikheten att de möts?
Låt oss titta på personen som kom till platsen först. Han var på plats under tre minuter någonstans i tidsintervallet mellan 09.30 och 10.03. Notera att han inte behövde komma ett helt antal minuter efter 09.30, utan vilket tidpunkt som helst skulle kunna fungera som startpunkt. Dessutom vet vi att alla startpunkter mellan 9.30 och 10.00 var exakt lika sannolika.
Personen som kom senare kunde också ha varit på plats från klockan 9.30. Vi kan markera den första personens ankomstpunkt på x-axeln och den andra personens ankomstpunkt på y-axeln. Då kommer varje par (x,y) motsvara en punkt i nedre halvan av kvadraten av format 33×33 och alla punkter har lika stor sannolikhet att motsvara personernas starttider!
Personerna träffas om den som kommer senare kommer inom 3 minuter från den förstas ankomst. Det motsvarar punkterna i det gröna parallelltrapetset:
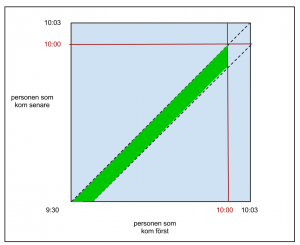
Då kan vi beräkna sannolikheten för att personerna faktiskt möts: den är lika med trapetsets area genom halva kvadratens (alla positiva utfall genom alla möjliga utfall).
Parallellogrammen som kompletterar trapetset har arean 3*30 = 90.
Lilla triangeln som vi måste ta bort för att få trapetsets area har arean 3*3/2 = 4,5.
Halva stora kvadratens area är 30*30/2 = 450.
Totalt är sannolikheten alltså lika med (90-4,5)/450 = 0,19



Hej,
Kan man inte bara ta antalet minuter som personerna kan anlända på (kl 9,30 – 10,00 = 31 min) och dela detta med antalet minuter som de båda vistas på platsen (6 Min), alltså: 6/31 = 0,19354… som motsvarar en sannolikhet på ca 19%.
/K
Nja, i detta fall ger det på ett ungefär rätt svar, men jag ser inte varför detta skulle fungera i allmänhet. Till exempel om det skulle kunna vara på plats mellan 10:30 och 10:37 så är sannolikheten 33/49 (ca 67%) att träffas, samtidigt som din metod ger svaret 75%.
Kristians lösning verkar vara en bra lösning asymptotiskt, om vi antar att tiden då de potentiellt kan anlända är N minuter så borde sannolikheten att de träffas vara ca 6/N+O(1/N^2). Om vi antar att person A anländer vid tid a och person B lämnar platsen vid tid b så måste 0<b-a<6 för att de ska träffas. Dvs, b måste ligga i intervallet a,a+6. Vi har ett 6 minuters intervall på en total tid av N. Vi missar en del i kantfallen då t.ex a anländer vid tiden N så kan inte B lämna vid tid N+5 då intervallet blir avhugget. Detta kan dock begränsas av k/N^2.
Geometriskt sett så är detta uppenbart då din strimma har längd ca N och höjd 3 och alltså area ungefär 3N (där det igen är kanten som ställer till det).