Bollförrådet
I förrådet till gympasalen låg fotbollar och volleybollar, lika många bollar av varje sort. Gympaläraren skulle anordna en volleybollturnering, och när han hade tagit ut några volleybollar, så låg det kvar 7 gånger så många fotbollar som volleybollar i förrådet. Några elever kom för sent och fick leka vad de ville. Efter att de hade hämtat tre bollar till låg det kvar 20 gånger så många fotbollar som volleybollar i förrådet. Hur många bollar låg i förrådet från början?
Ett fotbollslag
Ett fotbollslag
I ett fotbollslag med 11 spelare är genomsnittsåldern 22 år. Under matchen fick en av spelarna en skada och var tvungen att lämna planen. Då blev genomsnittsåldern för spelarna på planen 21 år. Hur gammal var spelaren som fick skadan?
Problem vecka 21
Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3 mål i matchen
Efter matchen visade det sig att exakt tre prognoser stämde. Vad blev matchens resultat?
Dvärgarna (4 poäng).
Draken fångade sex dvärgar, låste in dem i sin grotta och sade till dem: ”Jag har sju hattar som har var sin färg: röd, orange, gul, grön, blå, lila och vit. Imorgon vid gryningen kommer jag att binda för era ögon och sätta var sin hatt på er och en hatt gömmer jag. Efter det kommer ni att kunna se, men ni får inte längre prata med varandra. Sedan får var och en viska till mig, vilken färg det är som saknas. Om åtminstone tre stycken gissar rätt, befrias ni alla. Om färre gissar rätt, äter jag upp er alla.”
Vad ska dvärgarna bestämma innan gryningen, för att rädda sig själva?
Rutnätet (6 poäng).
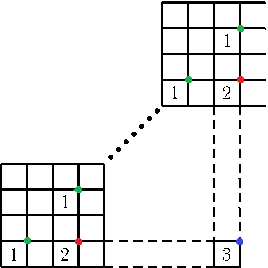
Varje punkt med heltalskoordinater på planet målades i en av tre färger. Visa att det går att hitta en likbent rätvinklig triangel med hörn i punkter med heltalskoordinater, som är målade i samma färg.
Visa lösningar
Lösningen till problemet för de yngre vecka 44
Mattegåta
Fem fotbollslag spelade en turnering, där alla lag mötte alla en gång. För en vinst tilldelades 3 poäng, för oavgjort 1 poäng och för förlust gavs inga poäng.
Fyra av lagen fick 1, 2, 5 och 7 poäng respektive. Hur många poäng fick det femte laget?
Diskussion
I alla för mig blir det lättare att lösa turneringsproblem, om man ritar en graf eller en tabell över resultaten.
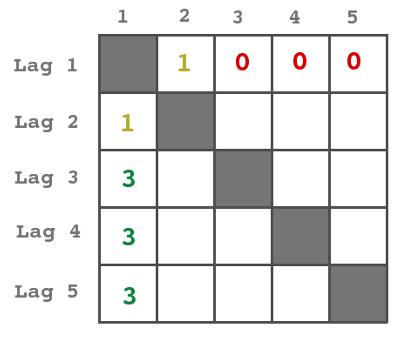
Till exempel vet vi att ett av lagen fick 1 poäng, då kan man utan inskränkning anta att det är Lag 1. Då ser deras rad i tabellen ut som nedan.
Kolonnen är på sätt och vis motsatsen, alla förluster byts mot vinster (Lag 3, 4 och 5 vann ju mot Lag 1). Problemet går ut på att ta reda på sista radens poängsumma!
Lösning (av Nicklas Yttergren, kompletterad)
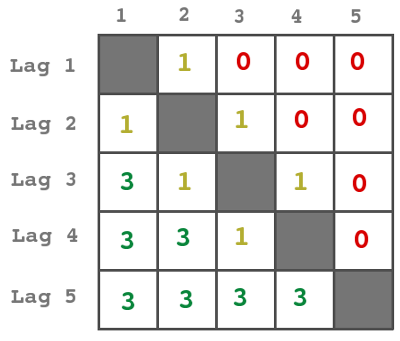
Observera hur många matcher har förlorats och hur många vunnits, de måste ha varit lika många. Totalt var det 7 förluster och 3 vinster utan att man räknat med med det femte laget (det ser man på poängen 1=1+0+0+0, 2=1+1+0+0, 5=3+1+1+0, 7=3+3+1+0).
Då måste det femte laget vunnit alla sina matcher, eftersom de spelade fyra och det är precis så många vinster som saknas. Därför fick de 12 poäng.
Matteproblem för de yngre vecka 44
Mattegåta
Fem fotbollslag spelade en turnering, där alla lag mötte alla en gång. För en vinst tilldelades 3 poäng, för oavgjort 1 poäng och för förlust gavs inga poäng.
Fyra av lagen fick 1, 2, 5 och 7 poäng respektive. Hur många poäng fick det femte laget?
Lösning till problem vecka 19
En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en fotboll?
Man kan anta att Eulerkarakteristiken på fotbollen är 2 och arbeta utifrån det, om man nu vet vad Eulerkarakteristik är för något. Med nedan använder jag mig av Thomas lösning.
Lösning:
Det finns S svarta lappar och V vita lappar. Totalt finns det 32 st, så S + V = 32.
För varje svart lapp finns 5 vita lappar runt den, men varje vit lapp ligger intill 3 svarta, så 5S räknar varje vit lapp 3 gånger och vi får 5S / 3 = V
Och S + 5S/3 = 32, det vill säga 3S + 5S = 96 och då är S = 12, V = 20. Alltså finns 20 vita lappar.
Matteproblem vecka 19
En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en fotboll?