Etikett: motsägelsebevis

Ett tal med åtta siffror

Ett tal med åtta siffror

[kkratings]

Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?

Visa lösningen

Problem vecka 21

Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3 mål i matchen

Efter matchen visade det sig att exakt tre prognoser stämde. Vad blev matchens resultat?

Dvärgarna (4 poäng).
Draken fångade sex dvärgar, låste in dem i sin grotta och sade till dem: ”Jag har sju hattar som har var sin färg: röd, orange, gul, grön, blå, lila och vit. Imorgon vid gryningen kommer jag att binda för era ögon och sätta var sin hatt på er och en hatt gömmer jag. Efter det kommer ni att kunna se, men ni får inte längre prata med varandra. Sedan får var och en viska till mig, vilken färg det är som saknas. Om åtminstone tre stycken gissar rätt, befrias ni alla. Om färre gissar rätt, äter jag upp er alla.”

Vad ska dvärgarna bestämma innan gryningen, för att rädda sig själva?

Rutnätet (6 poäng).
Varje punkt med heltalskoordinater på planet målades i en av tre färger. Visa att det går att hitta en likbent rätvinklig triangel med hörn i punkter med heltalskoordinater, som är målade i samma färg.

Visa lösningar

Lösningen till problemet för de äldre vecka 40

Mattegåta

Det finns fyra positiva heltal: a, b, c, d. Deras minsta gemensamma multipel råkar vara lika med a+b+c+d. Visa att abcd är delbart med 3 eller 5 (eller både 3 och 5).

Diskussion

Typiskt problem som kräver motsägelsebevis. Ett första steg är att inse att inget av talen a, b, c eller d får vara delbara med vare sig 3 eller 5 för att produkten inte ska vara det.

Eftersom problemets formulering inte skiljer på a, b, c och d (vi kan byta plats på två av dess bokstäver och få exakt samma problem), kan vi bestämma storleksordningen mellan dem till exempel.

Lösning

Antag att abcd är delbart med varken 3 eller 5.

Utan inskränkning kan vi anta att a>=b>=c>=d. Då kan a+b+c+d maximalt vara 4a (för a är störst).

Samtidigt vet vi att a+b+c+d är den minsta gemensamma multipeln till a, b, c och d. Så summan är delbar med alla dem var för sig, så bland annat a. Detta tillsammans med förra stycket medför att a+b+c+d är antingen lika med a, 2a, 3a eller 4a.

Fall I. a+b+c+d=4a. Men då är alla talen lika med a för att komma upp i den summan. I så fall skulle MGM(a, a, a, a)=a som inte är lika med 4a. Motsägelse.

Fall II. a+b+c+d=3a. Men då är 3a den minsta gemensamma multipeln till talen, det vill säga faktorn 3 behövs. Så något av talen måste vara delbart med 3.

Fall III (det svåraste fallet). a+b+c+d=2a. Så b+c+d=a, och eftersom b var det näst största talet, så är b minst en tredjedel utav a. Dessutom är b en delare till 2a. Således får vi begränsat med alternativ vad b kan vara.

Nämligen kan b vara lika med a/3 eller 2a/3 eller a/2 eller a (någon delare av större än dess tredjedel eller en dubblerad delare till a). De förstå två varianterna innebär att a är delbart med 3, vilket leder till motsägelse. Det sista fallet innebär c=d=0, vilket inte de får vara.

Vi får kvar att b=a/2. Så c+d=a/2 (för att hela summan ska bli 2a). Och c är störst av c och d, så c måste vara minst a/4. Kom ihåg att c också är delare till 2a, som var MGM för talen. Så c kan vara a/4 eller 2a/4 eller 2a/5 eller 2a/6 eller 2a/7.

Ifall c=a/4 så är d=a/4 (för att hela summan ska bli a). Men då är MGM(a, a/2, a/4, a/4)=a och inte 2a. Ifall c=2a/4=a/2, måste d=0, vilket inte går. Ifall c=2a/5 eller c=2a/6=a/3 medför att a är delbart med 3 eller 5, motsägelse. Så c=2a/7.

Då kan vi räkna ut att d=3a/14. Men då är ju d en multipel av 3.

Fall IV. a+b+c+d=a. Då är b=c=d=0. Det får de inte vara!

Nu är alla fall undersökta. Vi har fått motsägelse varenda gång, alltså var vårt antagande fel från början. Någon utan a, b, c eller d måste vara delbar med 3 eller 5, alltså är abcd delbart med 3 eller 5.

Kommentera gärna om jag glömt något fall.

Lösning till problem vecka 23

En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta sidan vrida sig 90 grader i förhållande till startläget?

Svar:

Nej, det kunde den inte.

Lösning:

Låt oss beteckna kubens hörn med A, B, C, D, A_1, B_1, C_1, D_1 (sidan A_1B_1C_1D_1 ligger precis under sidan ABCD). Föreställ er att finns en liten tetraeder ACB_1D_1 som är gjord av ett annat material. Vi kommer att följa den tetraederns position allt eftersom tärningen rör sig.

Om tärningen rullas över en gång, kommer tetraedern befinna sig i samma läge som BDA_1C_1 hade från början, fast parallellfärflyttad. Och vice versa, BDA_1C_1 avbildas på en parallellförflyttning av tetraedern ACB_1D_1.

För att tärningen ska komma tillbaka tillsamma ruta, måste den rullas ett jämnt antal gånger (föreställ er ett schackbräde på bordet, då byter rutan färg efter varje steg). Det innebär att den annorlunda tetraedern kommer att avbildas på sig själv.

Men om den översta sidan vrids 90 grader, så avbildas sidan AC på sidan BD, men den sistnämnda ligger utanför tetraedern av annorlunda material. Motsägelse.

Klassiska bevis: Cevas sats, del 2

Detta inlägg är fortsättning på del 1 om Cevas sats. Första delen förklarar satsens formulering och ger tips för hur man skulle kunna bevisa den. Den här delen innehåller själva beviset.

Cevas sats

Given är en triangel ABC. Tre cevianer AM, BL och CK skär varandra i samma punkt om och endast om \frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1

Bevis:

Antag först att cevianerna skär varandra i en och samma punkt O. Vi skall visa att värdet av uttrycket verkligen är 1.

Notera till exempel att trianglarna COM och MOB har lika stora höjder utgående från punkten O, eftersom deras baser ligger på samma linje. Låt höjderna ha längden h. Därför kan vi enkelt uttrycka förhållandet mellan dessa två areor:

\frac{S_{COM}}{S_{MOB}}=\frac{\frac{CM\cdot h}{2}}{\frac{MB\cdot h}{2}} = \frac{CM}{MB}

Eftersom trianglarna CAM och MAB också har lika långa höjder, utgående från A, så kommer deras areor också att förhålla sig som  \frac{CM}{MB}.

COM_MOB CAM_MAB

Låt  \frac{CM}{MB} = k (något reellt tal). Men om S_{CAM} är k gånger större än S_{MAB} och S_{COM} är k gånger större än S_{MOB}, så är differensen, S_{COA}, också k gånger större än S_{AOB}

Det vill säga \frac{S_{COA}}{S_{AOB}}=\frac{CM}{MB}

Med analogiska resonemang får vi förhållanden mellan de andra par av de färgade trianglarna:

\frac{S_{AOB}}{S_{BOC}}=\frac{AL}{LC}
\frac{S_{BOC}}{S_{COA}}=\frac{BK}{KA}

Därför kan vi skriva om uttrycket:

\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=\frac{S_{AO B}}{S_{BOC}}\cdot\frac{S_{COA}}{S_{AOB}}\cdot\frac{S_{BOC}}{S_{COA }}=1

eftersom allt förkortas i det omskrivna uttrycket.

Nu har vi kvar att bevisa att värdet på uttrycket inte kan vara 1 utan att cevianerna skär varandra. Vi antar motsatsen, det vill säga att värdet är 1, men cevianerna råkade inte skära varandra i samma punkt:

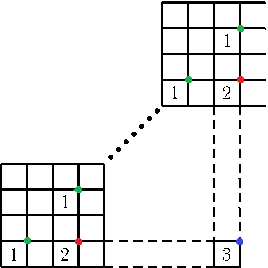
trefulacevianerNu är vi så smarta som möjligt och använder oss av del 1, som vi redan har bevisat. Precis som i följande berättelse:

En matematiker och en fysiker löser praktiska uppgifter. De blev tillsagda att koka upp 1 liter vatten med hjälp av en vattenkran och en vattenkokare. Båda fyller förstås sin vattenkokare med vatten och sätter på den.

Nästa uppgift är annorlunda: de får en vattenkokare full med vatten och ska nu igen koka upp 1 liter vatten.

Vad gör en fysiker? Han ställer vattenkokaren på plattan och sätter på den förstås.

Vad gör en matematiker? Han häller ut vattnet och därmed ska han lösa praktisk uppgift nummer ett, vilket han redan kan.

I detta fall är det förstås inga onödigheter vi sysslar med. Men på samma sätt som i berättelsen ska vi göra någonting, för att kunna använda oss av tidigare kunskaper. Vi drar en ny linje, för att få samma situation som förut. Dra linjen CK’, som går igenom skärningspunkten för cevianerna AM och BL.

fyracevianer

Från del 1 vet vi att följande måste gälla:

\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK'}{K'A}=1

Men enligt antagandet har vi också

\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1

Bland annat är uttrycken lika med varandra och på så sätt får vi  \frac{BK'}{K'A}=\frac{BK}{KA}, vilket i sin tur implicerar att BK'\cdot KA=K'A\cdot BK, vilket är omöjligt, eftersom BK<BK’ och K’A<KA. Motsägelse, alltså var situationen omöjlig!

Således så fort uttrycket är lika med 1, så måste cevianerna skära varandra i en punkt.

Användningar för satsen

På så sätt har vi i princip bevisat flera satser på en gång, till exempel att medianerna i en triangel skär varandra i en och samma punkt. Samma sak gäller för bisektriserna, samma för linjer som förbinder hörn och tangeringspunkter för den inskrivna cirkeln. Det lämnas åt läsaren att komma på hur man ska använda Cevas sats för att visa de egenskaperna.

Spel på en remsa

Rekommenderad från: 15 år

[kkratings]

Det finns en rutig remsa 1xn:

remsa

Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två kryss hamna bredvid varandra och inte heller två ringar. Spelaren, som inte kan göra ett drag när det är hans tur, förlorar.

Anders gör det första draget. Vem har ett vinnarstrategi, det vill säga vem kan alltid vinna oavsett hur motståndaren spelar?

Observera att svaret kan bero på talen n, som säger hur lång remsan är.

Visa lösningen

Mattecirkel: lektion i lådprincipen

Vår mattecirkel tuffar på vidare. Den är fortfarande med Anna, men eftersom jag tänkte skriva lite fiktion här, så skriver jag inte ut det i titeln.

För nyligen läste jag i en klok bok om hur man lär ut induktion. Bland annat fanns en påhittad dialog mellan en elev och en lärare där bådas tankegångar var klara. Man kunde se vanliga tankefel hos eleven och hur man kunde sätta eleven på rätt tankespår genom ledande frågor.

Den senaste gången handlade vår lektion om lådprincipen, som är även känd under namnet Dirichlets princip. Här är några av problemen som löstes:

1. a) Bland 22 elever finns fler pojkar än flickor. De sitter på rad. Visa att de finns minst ett par pojkar som sitter sida vid sida.
b) Bland 21 elever finns fler pojkar än flickor. De sitter på rad. Kan man vara säker på att det finns minst ett par pojkar som sitter sida vid sida?

2. Det finns 15 små hål i en maläten matta 4×4 m. Visa att man kan klippa ut en liten matta  av storlek 1×1 som är utan hål eller med ett hål på kanten.

3. a) Givet 10 positiva heltal, kan det hända att alla möjliga skillnaderna emellan dem är ej delbara med 10?
b) Givet 11 positiva heltal, kan det hända att alla möjliga skillnaderna emellan dem är ej delbara med 10?

Och här är ett (!) utav möjliga scenarion för en genomgång om lådprincipen.

Läraren: Tänk på följande problem. I en kasse ligger vita och svarta strumpor. Hur många strumpor måste man som minst ta upp ur kassen (om man måste dra på måfå) för att garanterat få upp två strumpor av samma färg?

…

Eleven: Det måste ju vara 3 strumpor! Har vi maximalt otur kommer de första två strumporna vara av olika färger. Men då måste den tredje ha samma färg som nån av de första två. Så minsta antalet är 3 strumpor.

Läraren: Helt rätt! Men var försiktig med vad du menar med ”maximal otur”. Till exempel, att först dra upp en vit strumpa och sedan en svart eller lika mycket otur som att först dra upp en svart strumpa och sedan dra upp en vit. Och i uppgiften är det inte viktigt att få upp strumporna så snabbt som möjligt, utan vara säker på att dra upp två lika för ett visst antal.

Nästa fråga: I en studentkorrior på 5 rum bor 6 personer. Visa att det finns ett rum med minst två personer.

Eleven: Enkelt! Sätter man in 1 person i varje rum så blir det 1 över och då måste den personen flytta in i något rum där det redan finns nån!

Läraren: Men varför måste det vara minst 1 person i varje rum, det stod det inget om i villkoren?

Eleven: Nej, ok, men det var det sämsta möjliga fallet.

Läraren: På sätt och vis är väl alla fallen ”sämst” hur vi än gör, det blir ju minst 2 personer i något rum i alla fall? Varför skulle vi inte kunna omplacera personerna på något smart sätt så att det inte behöver vara 2 eller fler i något rum?

Eleven: Men det går ju inte! Om något rum blir tomt, så måste det bli fler med ett annat!

Läraren: Men nu utgår du ändå från att du först placerar in 1 person i varje rum.

Eleven: Ok, jag börjar om från början. Om det är 0 eller 1 personer placerade i varje rum, så räcker inte rummen till för 6 personer.

Läraren: Precis! Nu har du i stort sett bevisat lådprincipen. Om det finns n stycken rum och fler än n personer, och personerna bor i rummen, så måste något rum ha minst 2 personer. Eller, i en mer välkänd version:

Om n lådor innehåller minst n+1 duvor, så innehåller någon låda minst 2 duvor.

Bevis är precis som i problemet. Om varje låda skulle innehålla maximalt 1 duva, skulle n lådor maximalt innehålla n duvor. Motsägelse.

Lektioner fortsätter på liknande sätt och problemen ökar i svårighetsgrad. Problem nummer 2 skulle kunna vara följande:

I en granskog växer en miljon granar. Varje gran har som mest 200000 barr. Visa att det finns två träd i skogen med samma antal barr.

Oftast är det bra att poängtera när man går igenom lösningen vad som är lådor och vad som är duvor. Det är inte så självklart i problemen från utdraget ovan. Notera också att man oftast drar igenom beviset för lådprincipen varje gång istället för att bara citera den. Det är essentiellt för förståelsen av principen.

Klassiska bevis: roten ur 2 irrationellt

Flera av mina bekanta har berättat för mig vad deras första möte med riktiga matematiska bevis var. Och man märker kanske inte först att det man läser eller hör om är så kallade riktiga bevis, förrän man läser ordet ”bevis” explicit. De första sådana för var och en kunde ha varit bevis för Pythagoras sats, något induktionsbevis eller motsägelsebevis.

Här tänkte jag berätta om den mest klassiska klassikern av motsägelsebevis, nämligen att roten ur 2 är ett irrationellt tal.

Vad betyder irrationellt?

Ett irrationellt tal är ett tal som inte går att få med hjälp av naturliga tal 0, 1, 2, 3 …. och de aritmetiska operationerna +, -, * och /. Talen som däremot går att få på det sättet kallas rationella, till exempel \frac{(5-10)}{3}=\frac{-5}{3}. Rationella tal kan alltså skrivas som bråk.

Irrationell och rationell är helt enkelt motsatser. På grund av den här negativa definitionen (det vill säga definiera något genom att använda ett ”inte”), är det naturligt med ett negativt bevis till påståendet (det vill säga motsägelsebevis).

Påstående: \sqrt2 är ett irrationellt tal.

Tankegång: Vi skall alltså bevisa att \sqrt2 inte är ett rationellt tal. Kan verka svårt först, vi kan ju inte riktigt testa alla möjligheter, alla bråk som överhuvudtaget går att få fram. T.ex. (bara ett exempel nu, helt onödigt för beviset!!!):

Är \sqrt2=\frac{3}{2}? Nej, för då skulle deras kvadrater vara lika 2=\frac{9}{4}, vilket absolut inte är sant!

Men det finns oändligt många bråk, vi kan sitta och gissa bråk som är ungefär lika med roten ur 2 och sedan verifiera att de inte är exakt lika. Men bara för att vi inte kan hitta något bevisar inte att det inte finns!

Det är nu vi inser att det faktiskt skulle vara lättare att på något sätt testa alla möjligheter samtidigt. Med det menar jag att vi antar att det finns ett sådant bråk och vi sedan kommer fram till att det aldrig kan bli likhet med roten ur 2. Det är kärnan i alla så kallade motsägelsebevis: antag att det går (antag det positiva påståendet, det utan ”inte”) och kom fram till motsägelse.

Bevis: Antag att roten ur 2 är lika med något bråk. Förkorta bråket så långt det går, så att nämnaren och täljaren inte längre går att dela med samma heltal. Vi har alltså nu:

\sqrt2=\frac{a}{b} och a och b är heltal som inte har någon gemensam delare.

Som förut försöker vi kontrollera likheten genom att kvadrera:

2=\frac{a^2}{b^2},

så

2{b^2}=a^2.

Varför är denna likhet omöjligt då? Vi tar hjälp av talteori, läran om heltal och delbarheter.

Vänsterledet 2b^2 är ett jämnt tal, så högerledet, a^2 måste vara det också. Alltså går a att dela med 2, dvs a=2k, där k är ett heltal. Skriv om likheten:

2{b^2}=(2k)^2=4k^2.

MEN detta innebär ju att b^2=2k^2 så med samma resonemang som förut får vi att b är ett jämnt tal. Men nu kommer vi fram till motsägelse, eftersom i situtationen då både a och b är jämna går det faktiskt att förkorta bråket (med 2). Nu är vi faktiskt klara.

Vi blev klara så fort vi fick motsägelse i vår lösning. Det är därför det heter motsägelsebevis.

© 2009-2024 Mattebloggen