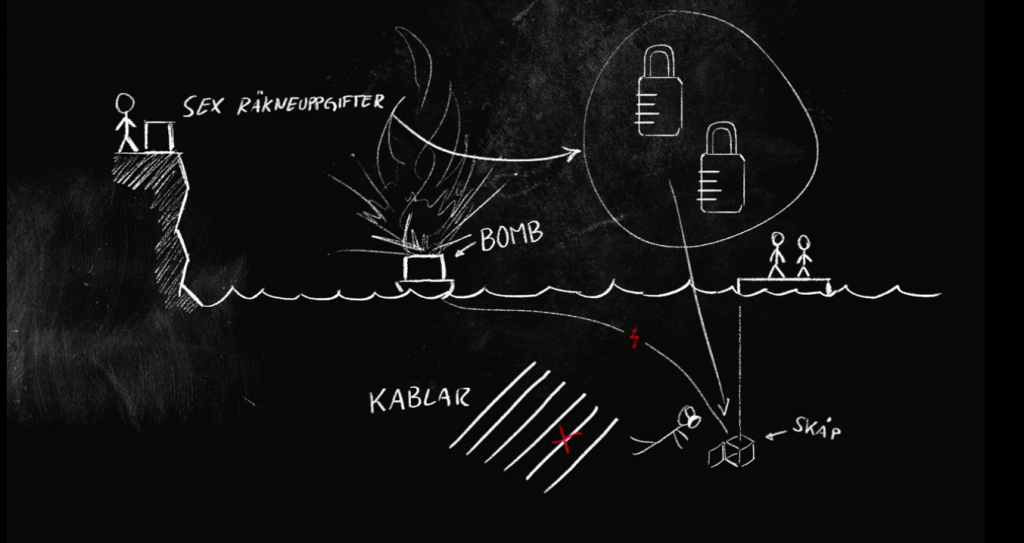
Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de alla.
Kodlås 1 bestod av tre uppgifter, där varje uppgift gav en siffra. Den tresiffriga koden skulle låsa upp det första låset under vatten.
Kodlås 2 gav på samma sätt ett tresiffrigt kod till andra låset.
Kablar 5 uppgifter gav 5 siffersvar, där 0 stod för A, 1 stod för B och så vidare till 9 som stod för J. Bokstäverna var kopplade till kablar som var safe att klippa av.
Kodlås 1
sifferkod 1
Sofie och Maria är syskon. För deras åldrar gäller följande samband: Summan är lika stor som produkten. Hur gamla är Sofia och Maria?
Addera talen.
Det här var enda uppgiften vi först gjorde fel på!
Den går ut på lista ut åldrarna S och M sådana att S+M = S·M.
Ekvationen S·M − S − M = 0 beskriver en hyperbel, som har oändligt många punkter. Men eftersom vi frågas efter heltalslösningar (och det bara ska vara en lösning som funkar), så funkar det bra att gissa.
Vi gissade på 0+0 = 0·0, men 2+2 = 2·2 funkar också. Det senare betraktas troligare som ålder (kanske säger man aldrig att någon är 0 år gammal), så svaret var 4 (och inte 0 som vi först trodde).
Första kodlåssiffran är 4.
sifferkod 2
En tjuv stal en säck med guldmynt i ett slott. För att komma ut ur slottet måste han passera tre vakter. Den första mutade han genom att ge vakten hälften av guldmynten. Vakten gav dock tillbaka 100 guldmynt av ren medkänsla. Den andra vakten fick hälften av tjuvens pengar men gav sedan tillbaka 50 guldmynt. Den tredje vakten fick hälften av pengarna men gav sedan tillbaka 25 guldmynt. Tjuven hade då 100 guldmynt kvar. Hur många mynt hade han från början?
Dividera svaret med 40.
Här är det lättast att gå baklänges. Tjuven hade 100 guldmynt i slutet.
Nu kollar vi hur mycket han hade innan varje händelse:
Innan tredje vakten gav honom 25 mynt hade han alltså 75 mynt (100-25).
Innan tredje vakten fick hälften av pengarna hade tjuven 150 mynt (75*2).
Innan andra vakten gav honom 50 mynt hade han 100 mynt (150-50).
Innan andra vakten gick hälften av pengarna hade han 200 mynt (100*2).
Innan första vakten gav honom 100 mynt hade han 100 mynt (200-100).
Innan första vakten fick hälften av pengarna hade han 200 mynt (100*2).
200/40 = 5.
Andra kodlåssiffran är 5.
sifferkod 3
Ett tåg består av ett lok och fem vagnar (A, B, C, D och E). På hur många sätt kan vagnarna ordnas så att vagn A kommer närmare loket än vagn B kommer?
Dividera svaret med antalet konsonanter i det svenska alfabetet.
Det går att ställa vagnarna på rad på 5! sätt. 5! står för uttrycket 5*4*3*2*1 = 120.
Detta beror på att en av de fem vagnarna kan ställas längst fram, en av de fyra kvarstående kan ställas på andra plats, en av de tre kvarstående på tredje plats, en av de två som är kvar kan ställas näst sist och ett alternativ har vi kvar för den vagnen som ska stå sist.
Exakt hälften av de ordningarna är sådana att A kommer närmare loket än B (och exakt hälften är tvärtom). Det beror på att alla ordningar kan paras ihop: varje ordning är i par med nästan samma ordning, fast där A och B har bytt plats. Till exempel är CADEB i par med CBDEA. Därför ska vi dela svaret med 2.
(Det här är för övrigt i stort sett samma uppgift som 2(a) här: LÄNK http://mattebloggen.com/wp-content/uploads/2014/09/Lektion2Permutationer.pdf)
120 / 2 = 60.
I det svenska alfabetet finns det 20 konsonanter (29 bokstäver totalt, varav 9 är vokaler).
60 / 20 = 3.
Tredje kodlåssiffran är 3.
Kodlås 2
sifferkod 1
Sofie satt på balkongen och gjorde sin matteläxa. Hon hade just skrivit svaret på en uppgift, när en duva kom flygande och lämnade sitt ”visitkort”, så att sista siffran (= entals siffran) i svaret inte syntes. Skillnaden mellan det ursprungliga svaret och det svar som nu syntes var 276. Vilket var det ursprungliga svaret?
Addera svarets siffror.
Om det ursprungliga slutsiffra var A, så kan talet skrivas som 10*X + A (oavsett hur många siffror talet har kan de skrivas som ett visst antal tiotal plus en slutsiffra).
När duvan har varit framme och busat hade Sofie talet X framme (antalet tiotal i det ursprungliga talet).
Det betyder att 10*X + A – X = 276
Det vill säga 9*X + A = 276.
Talet 276 är inte med i nians tabell, utan ger rest 6 när man dividerar med 9. Det betyder att A måste ha varit 6 och X i sin tur måste ha varit 30 (=270/9).
Så talet som stod där från början var 306 (=10*30+6). Detta är det enda svaret.
3+0+6 = 9
Första kodlåssiffran är 9.
sifferkod 2
Tre positiva heltal (naturliga tal) är så beskaffade, att om vart och ett multipliceras med de två övrigas summa, får man produkterna 120, 133 och 169. Bestäm talen.
Addera dessa tre tal och subtrahera det med det tal som kommer efter 13 i Fibonaccis talföljd.
Vi har tre tal som vi kan beteckna med a, b och c. Då vet vi att:
a*(b+c) = 120
b*(a+c) = 133
c*(a+b) = 169
Sen ska man bestämma talen står det, men det struntade vi i! Man skulle nämligen addera dessa tre tal senare, så vi fokuserade på att bestämma a+b+c (så man behöver inte bestämma vart och ett av talen).
c*(a+b) = 169. Eftersom 13*13 = 169 och 13 är ett primtal, går det bara skriva 169 som en produkt av tåv positiva heltal på två sätt:
169 = 13*13
169 = 1*169.
I det första fallet får vi att a+b+c = 13+13 = 26
I det andra fallet får vi att a+b+c = 1+169 = 170
Resan nu inser man att det är det första som är rätt (eftersom vi ska subtrahera 21 och få en siffra, men vi bevisar det korrekta svaret ändå utan att använda det).
133 = 7*19 och 7 och 19 är primtal, därav a+b+c är antingen 7+19=26 eller 1+133=134, så det måste vara 26!
(Detta stämmer även med faktoriseringen av 120 = 20*6 till exempel. Nu kan vi bestämma a, b och c för sig men det är för mycket jobb).
Fibonaccis talföljd är 1,1,2,3,5,8,13,21,34 och så vidare. Varje tal från och med det tredje är lika med summan av de två talen innan. Läs coola grejer om Fibonaccitalen
26 – 21 = 5
Andra kodlåssiffran är 5.
sifferkod 3
((√256 x 20 − 252 + 152 + 34) x 10) / 5 =
Det här är bara en vanlig uträkning. Men man kan ändå räkna ut det lite smart:
Då 256 är 2 upphöjt till 8, så är roten ur det 2 upphöjt till 4, det vill säga 16.
Multiplicerar man den stora parentesen med 10 och sedan dividerar med 5, så är det samma sak som att multiplicera parentesen med 2.
Sedan räknar man ut potenserna.
Då får man följande uttryck och du kan följa lite hur man kan tänka för att räkna snabbare:
(16*20 – 625 + 225 + 81)*2 =
(320 + 225 + 81 – 625)*2 =
(320 + 306 – 625)*2 =
(26 – 25)*2 =
1*2 = 2
Tredje kodlåssiffran är 2.
Kablar
Kabel 1
(6y-7)/4 + (3y-5)/7 = (5y+78)/28
Vad är y?
Detta är en vanlig ekvation, dessutom ser man att 28 är en minsta gemensam multipeln till 4 och 7, så det lättaste är att få bråken till gemensam nämnare:
7*(6y-7)/28 + 4*(3y-5)/28 = (5y+78)/28
Nu kan vi glömma bort 28:
7*(6y-7) + 4*(3y-5) = (5y+78)
Multiplicerar in talen:
42y – 49 + 12y – 20 = 5y + 78
Förenklar:
42y + 12y – 5y = 78 + 49 + 20
49y = 147
7y = 21
y = 3
Första kabeln ska ha bokstaven (3=)D.
Kabel 2
I herrtruppen till VM i cykel hade lagledare Hjulström tagit ut cyklister från enbart två klubbar – lika många från varje klubb. När det var dags för lagtempo, visade ett testlopp att alla åkarna i stort sett var jämngoda.
Hjulström beslöt därför att ta med två cyklister från vardera klubb i lagtempolaget. Ändå gav detta inte mindre än 36 tänkbara lagsammansättningar! Hur många cyklister bestod truppen av?
Den här uppgiften var inte det lättaste att tolka, så vi försökte tolka på ett sätt som skulle ge ett ensiffrigt svar.
Vi vet att det finns n cyklister i var och en av de två klubbarna. Om man ska räkna hur många sätt det finns att välja två stycken ur en klubb får man det från uttrycket n*(n-1)/2 (n sätt att välja den första, n-1 sätt att välja den andra, dela med två för att ordningen på de inte spelar roll, precis samma idé som i vagnuppgiften).
För att få antalet sätt att sätta ihop laget måste man multiplicera sätten att välja två från första klubben och två från andra klubben, vilket ska ge 36. Då n är densamma för båda klubbarna, innebär det att det ska finnas 6 sätt att välja två pers från en av klubbarna (för att 6*6=36).
Nu får vi uppställningen n*(n-1)/2 = 6, vilket betyder att n*(n-1)=12, så n måste vara lika med 4.
Så då är frågan om vi ska svara 8 eller 4. Troligen 8 eftersom det verkar som att man räknar in båda klubbarna i truppen.
Andra kabeln ska ha bokstaven (8=)I
Kabel 3
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
En vanlig uträkning till! Tur att man kan sina tvåpotenser:
210 = 1024
84 = (23)4 = 212 = 4096
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
8*1475 – 6600 – 4096 – 1024 – 79
Egentligen kan man bryta ut 8:an på tre ställen för att slippa räkna en stor multiplikation:
8*1475 – 8*825 – 8*512 – 8*128 – 79 =
= 8*(1475 – 825 – 512 – 128) – 79 =
= 8*(650 – 512 – 128) – 79 =
= 8*(138 – 128) – 79 =
= 8*10 – 79 =
= 80 – 79 =
= 1
Tredje kabeln ska ha bokstaven (1=)B
Kabel 4
Lille Micke sålde två fotbollskort för 21 kronor.
På det ena kortet tjänade han 10 % och på det andra kortet förlorade han 10 %.
Allt som allt tjänade han 5 %. Hur mycket hade varje fotbollskort kostat i inköp?
Svar: Addera dessa två tal och dividera summan med
den fjärde decimalen i pi.
Ett av de (till synes) svårare problemen! Lätt att virra ihop sig med procent. Men precis som i kodlåsproblemet med primtal behöver man inte lösa hela uppgiften. Vi ska ju använda summan av ursprungspriserna sedan, därför behöver vi egentligen inte ta reda på vart och ett av priserna, utan på vad det var tillsammans.
Om korten hade kostat A och B från början kan vi skriva villkoren som
21 = 1,1*A + 0,9*B = 1,05*(A + B).
Men om det är A+B vi är ute efter är uppgiftens andra rad helt onödig! Vi har:
21 = 1,05*(A + B)
A + B = 21/1,05 = 2100/105 = 300/15 = 100/5 = 20.
Och tur att man kan lite pidecimaler! 3,14159… Så svaret ska divideras med 5. 20/5 = 4.
Fjärde kabeln ska ha bokstaven (4=)E
Kabel 5
Då ett visst fyrsiffrigt tal multipliceras med fyra, får man ett nytt fyrsiffrigt
tal, där sifferföljden är omvänd jämfört med det första talet,
dvs. 4*ABCD = DCBA
Vilket är det ursprungliga talet?
Subtrahera svaret med 2004 och dividera den summan
med det tionde primtalet.
Här berättar jag en stor del av lösningen i tv. Men nu har jag chansen att kortfatta lösningen.
A = 1 eller 2, annars blir inte talet DCBA fyrsiffrigt. Då HL är jämnt, måste A = 2.
Då är D = 8 eller 9, annars är HL för litet (VL är minst 4*2000). Då 4*D ska sluta på A måste D = 8.
Vi har då 4*2BC8 = 8CB2.
Om vi fortsätter uträkningen med tiotal måste 4*C + 3 sluta på B. Samtidigt får inte B vara för stort (måste vara mindre än 3) för att multiplikationen 4*B00 inte ska ge ett till tusental.
Vi testar med olika C (i uppgiften är det inte givet att siffrorna A,B,C och D är olika även om det brukar vara så i sådana rebusar):
4*C + 3 = (”slutar på”) B
4*0 + 3 = 3 – för stort
4*1 + 3 = 7 – för stort
4*2 + 3 = 1
4*3 + 3 = 5 – för stort
4*4 + 3 = 9 – för stort
4*5 + 3 = 3 – för stort
4*6 + 3 = 7 – för stort
4*7 + 3 = 1 –
4*8 + 3 = 5 – för stort
4*9 + 3 = 9 – för stort
Då vet vi att B måste vara 1 och C är antingen 2 eller 7. Vi testar med båda:
4*2128 = 8512 – passar inte.
4*2178 = 8712 – passar!
Nu räknar vi ut kabelbokstaven:
2178 – 2004 = 174
Tur att man kan lite primtal: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…
Det tionde primtalet är alltså 29.
174/29 = 6 (egentligen hade man kunnat gå från slutet och testat de tio olika ursprungstalen 2004+0, 2004+29, 2004+29*2 och så vidare, men det är lätt att vara efterklok).
Fjärde kabeln ska ha bokstaven (6=)G
Vi var klara med uppgifterna lite innan motståndarbomben smällde (men höll på att kontrollräkna)!
Gillade du för övrigt sifferrebusen, kan du kolla upp några lite svårare här på bloggen: Granrebus, Sifferrebus, Palindromrebus och Trigonometrisk rebus.
