koordinatsystem – Mattebloggen

Schinzels sats

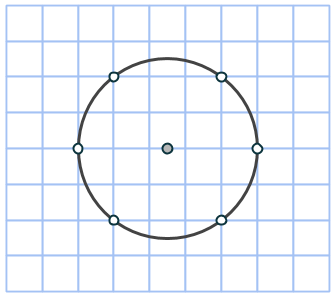
Har du läst om hur man hittar pythagoreiska tripplar i cirklar? I artikelserien träffar vi på många cirklar som har några punkter med heltalskoordinater på periferin.

Men oftast är antalet punkter delbart med 4 (cirkeln är centralsymmetrisk i förhållande till koordinatsystemet, eftersom mittpunkten ligger i vårt fall antingen i en heltalsnod eller i mitten av en ruta). Men kan vi hitta en cirkel med ett annat antal punkter på periferin, t.ex. 6?

Klicka här för svar

Vi vill alltså ta reda på för vilka n det går att hitta en cirkel som går igenom exakt n heltalspunkter.

Går det att hitta en cirkel med en heltalsnod på periferin? Så klart går det, vi kan t.ex. ta en cirkel med en väldigt liten radie som går igenom en godtycklig punkt.

Två heltalsnoder på periferin då? Ja, vi kan ju skapa cirklar som inte är rotationssymmetriska, men däremot spegelsymmetriska, genom att välja att ha mittpunkten på cirkeln i (0, 0.5) till exempel eller egentligen var som helst mellan två närliggande heltalsnoder. Tar vi radien lika med 0.5 så är vi garanterade att inga andra heltalsnoder än (0,0) och (0,1) kommer med på cirkelns periferi.

Hur gör vi med 3 punkter på periferin? Cirkeln får nu varken vara spegelsymmetrisk eller rotationssymmetrisk med avseende på heltalsnoderna (om två periferipunkter ligger strikt på vänstra/högra halvan av cirkeln). Således måste vi placera mittpunkten varken i en heltalspunkt eller i en ”halvtalspunkt”. Under några antaganden kan vi försöka hitta en cirkel med två heltalspunkter som befinner sig på samma vertikala linje. Vi antar att cirkelns horisontella diameter ligger på linjen y=0.

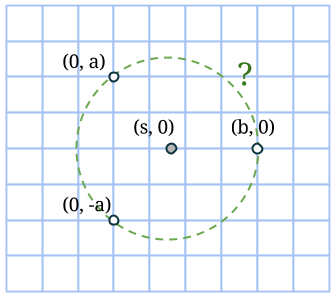
cirkel kanske 3 punkter

Koordinaterna för mittpunkten är då (s, 0) och för heltalsperiferipunkterna (0, a), (0, -a) samt (b, 0). Då får vi likhet av två radier (i kvadrat):

s² + a² = (b – s)²

s² + a² = b² – 2bs + s²

a² = b² – 2bs

Både a och b är positiva heltal, medan s är ett positivt reellt tal (förmodligen större än 1). Därför måste b vara åtminstone 3 och vi prövar b = 3.

Då måste a² = 9 – 6s. Tar vi a = 1 får vi s = 4/3 vilket ger oss cirkeln:

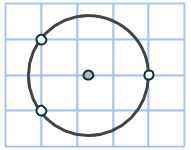
cirkel 3 punkter

Denna har exakt 3 punkter på periferin! Men hur gör man i det allmänna fallet? Kan man alltid få relativt snygga cirklar, det vill säga där punkterna ligger i par på respektive vertikallinjer? Det visar sig att man kan det med hjälp av Schinzels sats!

Schinzels sats

Det existerar en cirkel med exakt n heltalspunkter på periferin för varje naturligt tal n.

För jämna n=2k har Schinzels cirkel ekvationen

$(x-\frac{1}{2})^2 + y^2 = \frac{1}{4}5^{k-1}$

Medan för udda n=2k+1 har Schinzels cirkel ekvationen

$(x-\frac{1}{3})^2 + y^2 = \frac{1}{9}5^{2k}$

Testa till exempel hur cirkeln med exakt 7 heltalspunkter på periferin ser ut!

Schinzels cirklar är inte nödvändigtvis de minsta med den egenskapen, men de är i alla fall snygga på sättet beskrivet innan, nämligen att heltalspunkterna på periferin förekommer i par, vilket kan ses från ekvationen (mittpunkten ligger på en horisontell heltalslinje).

Kan du bevisa att Schinzels cirklar uppfyller egenskaperna som det påstås i satsen? Helt trivialt är det ju inte att bevisa.

Tack Sture Sjöstedt för frågeformuleringen, samt länkar och tips!

Lösningen till problemet för de äldre vecka 38

Mattegåta

En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.

Om S⁺ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S^– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S⁺-S^– lika med?

Diskussion

När problem handlar om att jämföra areor, så är det ofta så att delar av de här areorna är lika, speciellt när delarna har konstiga former (jämför med problemet för de yngre vecka 35).

Börja med att rita den enklare varianten (då cirkelns mitt är i första kvadranten) och försök att ta bort så många lika stora delar från S⁺ och S^– som möjligt och jämför det som blir kvar.

Lösning (av Johan Björklund, något modifierad)

Proof by picture:

Jag tillför två hjälplinjer paralella med koordinataxlarna genom (2a,2b). De är spegelbilder av koordinataxlarna speglade genom linjer (igenom parallella med koordinataxlar) genom (a,b).

Det är lätt att se att flera av områdena har lika area (markerat med bokstäver). De kommer att ta ut varandra när vi beräknar S⁺-S^– (S⁺ är den gula plus den rosa arean, medan S^– är den gula plus den blå). Kvar blir den centrala rektangeln med area 4ab.

Tillägg (av Erik Svensson)

Detta var ifall mittpunkten låg i den första kvadranten. Om den istället ligger i den tredje kvadranten, då är fallet uppenbart det samma efter rotation med ett halvt varv, och ifall mittpunkten ligger i andra eller fjärde kvadranten, då speglar vi i y- respektive x-axeln och får samma fall fast med S+ och S- ombytt, så att den sökta arean byter tecken.

Vi finner emellertid att just 2a * 2b ändå uttrycker arean i samtliga dessa fall.

Matteproblem för de äldre vecka 38

Mattegåta

En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.

Transformationsmatrisen – del 1

De flesta matematik- och ingenjörsstudenter läser någon form av linjär algebra. Det är ett högst rimlig inslag i deras utbildning – vilken vuxen människa räknar inte med matriser :)?

Just beräkningar är dessutom det studenterna måste lära sig först. Efter att de behärskat teknikerna som Gauss-elimination och matrismultiplikation är det dags för nästa steg: räkna med olika baser.

Jag har som lärare på kursen Linjär algebra II fått överlägset mest frågor om avsnittet som handlar om transformationsmatriser. De frågorna var jag också sämst på att besvara, eftersom man alltid är tvungen att hålla tungan rätt i mun med transformationsmatriser. Olika beteckningar i olika böcker förbättrar inte situationen.

Så vad är en transformationsmatris?

Med en transformationsmatris från basen b till basen c menar jag en matris som omvandlar vektorer, uttryckta i basen b, till likadana vektorer, men uttryckta i basen c.

Eller snarare så här: tar man en vektor (föreställ er ett geometriskt objekt) och skriver upp dess koordinater i basen b och sedan multiplicerar med transformationsmatrisen från vänster (det vill säga tar produkten matris $\cdot$ vektor), så kommer resultatet vara samma vektor (exakt samma geometriskt objekt), men koordinaterna kommer ändra sig. De kommer att vara uttryckta i basen c.

Därför kallas transformationsmatrisen också basbytesmatrisen. Det den gör är att byta vilken bas som för tillfället är den aktuella, i vilken bas vi just nu räknar saker.

Vissa begrepp kanske känns oklara i förklaringen ovan. Vi reder ut dem!

Vadå baser?

En bas kan ses som en sorts koordinatsystem. Om vi arbetar på det tvådimensionella planet så kan vi rita flera olika koordinatlinjer:

Som vi ser bestäms hela bilden alltid av två sorts linjer. Det är riktningarna på linjerna som är viktiga.

På samma sätt bestämmer två vektorer en bas i planet. De skall vara riktade åt olika håll (inte parallella). En bas är alltså ett par av vektorer. (Men i rum med högre dimension ska en bas bestå av fler vektorer, antalet är lika med dimensionen.)

Så exempel på baser (som vi ska jobba med) är:

Om vi lägger på koordinater på rutnätet kan vi läsa av vad de här basvektorerna har för koordinater (i standardbasen):

Nämligen $b_1=(2,0)$ , $b_2=(0,2)$ , $c_1=(2,0)$ , $c_2=(1,2)$ , $d_1=(1,-1)$ , $d_2=(1,1)$

Eller, skrivna på kollonform: $b_1=\left(\begin{array}{c}2 \\0\end{array} \right)$ , $b_2=\left(\begin{array}{c}0 \\2\end{array} \right)$ , $c_1=\left(\begin{array}{c}2 \\0\end{array} \right)$ , $c_2=\left(\begin{array}{c}1 \\2\end{array} \right)$ , $d_1=\left(\begin{array}{c}1 \\-1\end{array} \right)$ , $d_2=\left(\begin{array}{c}1 \\1\end{array} \right)$

Det är egentligen ingen väsentlig skillnad mellan radform och kolonnform, men oftast skriver man vektorerna på kolonnform. Om man gör det, så skall matrisen skrivas till vänster om vektorn vid multiplikation.

I nästa del reder vi ut hur man beräknar och skriver vektorer i olika baser.