Det här är fortsättningen på inläggen Transformationsmatrisen – del 1 och Transformationsmatrisen – del 2. I de två första delarna behandlades begreppen bas och vektorernas koordinater i olika baser.
Hur bestämmer man en transformationsmatris?
För att bestämma en matris, vilken som helst matris, är det ett nyttigt första steg att ta reda på matrisens storlek. Det vill säga hur många rader och kolonner den borde ha.
En mxn-matris är en matris med m rader och n kolonner. När en matrismultiplikation sker, händer följande med storlekarna:
mxn-matris gånger nxk-matris resulterar i en mxk-matris
Som ni ser äts det mittersta talet (n) upp, och de andra två kvarstår (m och k) och ger stoleken på resultatmatrisen.
I vårt fall känner vi inte till storleken på vänstraster matrisen (som ska bli transformationsmatrisen), men på de andra två (de är vektorer, kolonnvektorer, som är då kx1-matriser). De är, eftersom vi är i 2 dimensioner, 2×1 matriser.
Alltså: mxn matris gånger 2×1-matris resulterar i en 2×1-matris. Hmm, den siffran som äts upp är i alla fall 2, det vill säga n=2. Och m ska vara samma som den första siffran i resultat, så också 2.
Vi söker en 2×2-matris och en dum men ofta fungerande lösning är att köra brute force, det vill säga ansätta
Transformationsmatrisen=
Nu ska vi faktiskt minnas vad det var vi höll på med från början. Vi ville bestämma en matris som omvandlade vektorer från standardbasen till bas d.
Det ska alltså bland annat funka för själva basvektorerna.
Ett sätt
Som exempel kan vi välja standardbasvektorer, men jag väljer basvektorerna i basen d. Orsaken är att vi känner till koordinaterna för dem både i bas d, nämligen 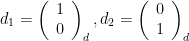 och i standardbasen, nämligen
och i standardbasen, nämligen 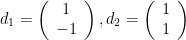 .
.
Vi kan då ställa upp:
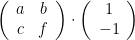 blir
blir 
samt
 blir
blir 
Och utförande matrismultiplikation som vanligt, även om a, b, c och f är okända, får vi:
a-b=1
c-f=0
a+b=0
c+f=1
Det ekvationssystemet kan vi lösa för hand: addera ekvationerna med a och b ledvis, då får vi 2a=1, så a=½, b=-½. På liknande sätt c=½, f=½.
Så transformationsmatrisen= .
.
Men man kan göra samma uppgift på flera olika sätt, detta glöms alldeles för ofta när man läser matematik.
Ett annat sätt
Vad händer till exempel om vi istället väljer standardbasvektorerna? De är vektorerna  och
och  i standardbasen, men vad är de i bas d? Vi kan gissa det eller räkna ut det, ett arbete som kommer löna sig ska det visa sig.
i standardbasen, men vad är de i bas d? Vi kan gissa det eller räkna ut det, ett arbete som kommer löna sig ska det visa sig.


vilket ger ekvationssystemet x+y=1, -x+y=0 (det liknar lite det vi fick i del 2), som i sin tur ger oss 2y=1 och således y=½, x=½ . På liknande sätt med andra standardbasvektorn:

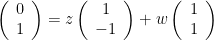 som ger ekvationssystemet z+w=0, -z+w=1, som ger 2w=1 och således w=½, z=-½ .
som ger ekvationssystemet z+w=0, -z+w=1, som ger 2w=1 och således w=½, z=-½ .
Bekanta tal, eller hur?
Vi har alltså  och
och 
Vad är då belöningen för denna möda?
Jo, om vi nu ställer upp matrisekvationen precis som innan, fast med nya vektorer, ser vi följande:
 blir
blir 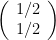
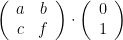 blir
blir 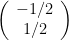
Och utför man matrismultiplikationen med variablerna får man:
a+0=½
c+0=½
0+b=-½
0+f=½
Praktiskt, eller hur? Utan mycket extra möda får vi igen 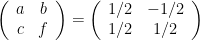
Det är just den här andra metoden man i allmänhet använder för att ta reda på transformationsmatriser generellt. Vi tittar på ett lite mer generellt fall i nästa del.