På ett område 1km x 1km växer en tallskog. Alla tallarna har diametern 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om det finns a) 1200 b) 4200 c) 4500 d) 4600 träd i skogen.
Vi använder oss av lådprincipen.
Försök att dela in hela skogen i ”lådor”, som en första gissning låt de vara 10m x 20m stora. Det får plats 100 * 50 = 5000 sådana gräsplättar i skogen, men de kan innehålla träd. Notera dock att ett träd kan ”sabba” maximalt fyra områden, om trädets mittpunkt finns precis i korsningen av fyra områden till exempel. Således kan 1200 träd sabba maximalt 4800 områden. Men då finns minst 200 osabbade områden. Fältbiologen kan välja och vraka!
Men hur ska man lösa problemet när det finns många fler träd? Vi nöjer oss med att lösa d), eller till och med för 4607 träd i skogen.
Antag att det finns 4607 träd i skogen. Dela upp skogen i områden 10,5 m x 20,5 m på följande sätt: 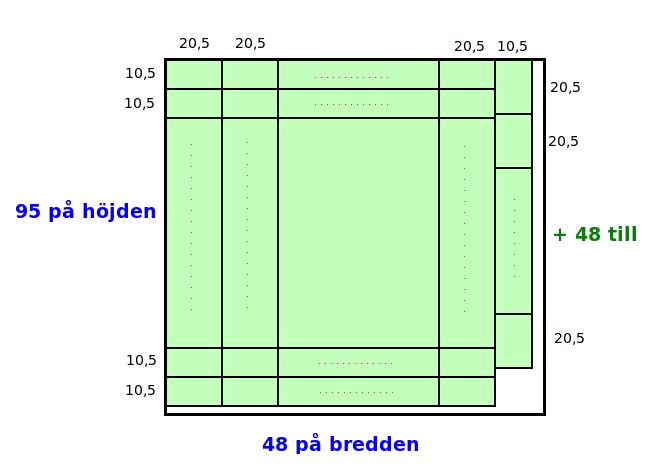
Det får plats med 48 stycken långsidor på bredden och då är det 16 meter kvar också. På höjden finns det plats för 95 stycken kortsidor och då är det 2,5 meter kvar. Det betyder att vi kan få in några fler områden i remsan som är kvar till höger, nämligen 48 stycken. Totalt fås 48 * 95 + 48 = 4608 områden, alla med storlek 10,5 m x 20,5 m. Men det betyder ju inte att det finns områden utan träd, för ett träd kan stå på fler områden samtidigt.
Men det finns åtminstone ett område utan ett trädcentrum uniti det på grund av lådprincipen (det finns 4607 trädcentrum, men 4608 områden). Vi tittar närmare på detta område:
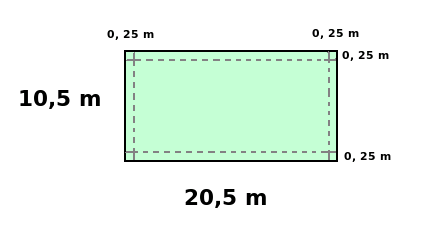
Om ett trädcentrum bara kan befinna sig utanför området, kan det bara ”intränga” på området med 25 cm. Den inträngningen sker från kanten. Alltså, om vi klipper bort 25 cm från varje sida, så är vi garanterade att ha trädfritt på det nya området. Vi har klippt bort 0,5 meter på varje håll, så det området som är kvar är precis 20m x 10m, vilket var precis det som behövdes!



