Mattebloggen

Mattebloggen har en inofficiell tävling i att lösa matematikproblem. Skicka in din lösning med motivering till valentina.chapovalova@gmail.com, så har du chansen att vara med på topplistan. Har du någon fråga om veckans problem, posta den i kommentarerna eller maila mig. Lycka till!

I en triangel ABC så är mitten av sidan AB markerad med punkten M. Även höjderna AH och BL är utritade. Det visade sig att triangeln MHL blev liksidig. Måste det vara så att även triangeln ABC är liksidig?

Om ja, ge ett bevis för varför den måste vara det. Om nej, visa hur ett motexempel konstrueras.

möjlig bild?

Det finns en platt kvadratisk tavla som är 1 dm x 1 dm stor. Vi säger att ett pappersark i form av en rektangel med area 2 dm^2 är ett omslag om man kan slå in tavlan i pappret så att båda sidorna täcks helt.

Både pappersarket 2 dm x 1 dm och papperskvadraten med sidan roten ur 2 dm är omslag.

(a) Hitta något annat omslag

(b) Visa att det finns oändligt många olika omslag

Lösning:

(a) Vi ska visa att rektangeln är ett omslag. Lägg rektangeln på kvadraten på så sätt att två av kvadratens hörn hamnar på långsidorna och ett tredje hörn hamnar i mitten på kortsidan som det ser ut på bilden.

Hur man viker biten vidare för att den ska omsluta kvadraten på båda sidor ser ni nedan:

(b) Dela upp kvadratens lodräta sidor i n delar. Då kan vi hitta en parallellogram, som omsluter kvadrattavlan. På bilden syns parallellogrammen med kortsidan (i detta fall n=5).

Sedan kan man göra om parallellogrammen till en rektangel, så att övertäckningen blir i princip densamma. Arean ändras fortfarande inte.

Notera att kvadraten fås när n=1, rektangeln när n=2, rektangeln när n=3:

n=3

Fredrik står i mitten av en rund gräsmatta, som har radien 100 meter. Varje steg Fredrik tar är 1 meter långt. Varje gång han ska ta ett nytt steg anger han riktningen som han ska gå i. Anna har då möjlighet att ändra Fredriks riktning mot den motsatta.

Kan Fredrik att komma på ett sätt att komma av gräsmattan oavsett vad Anna gör? Eller kan Anna alltid hindra honom?

Cissi klippte ut två likdana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.

Sedan slog Kalle in en spik i mitten av lådans botten. Kunde det bli så att spiken gick igenom ena figuren, men inte den andra?

Lösning

Detta är faktiskt möjligt att göra, på flera olika sätt! Låt oss se hur vi kan tänka för att konstruera ett exempel.

En figur skall täcka mittpunkten, men inte den andra. Samtidigt måste de vara ganska stora, för att tillsammans täcka hela bottnen. Så en lösning vore ju att låta en av figurerna ha ett hål i sig, som hamnar precis på bottnens mittpunkt.

Gör den figuren ganska stor och sedan gör en likadan figur, så att de täcker hela bottnen tillsammans. Så här kan det se ut:

Och här är figurerna ifyllda var för sig, så det syns att de täcker allt:

Spiken går genom den gröna figuren, men inte den rosa!

Låt F₁ vara en godtycklig konvex fyrhörning. För k>1, F_k konstrueras genom att man skär F_k-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs samma diagonal. Bestäm det största möjliga antalet icke-kongruenta fyrhörningar i följden {F_k}.

På ett område 1km x 1km växer en tallskog. Tallarna har alla diameter 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om det finns

a) 1200

b) 4200

c) 4500

d) 4600

träd i skogen.

Som taggen i inlägget antyder, så skall vi använda oss av lådprincipen. Försök att dela in hela skogen i ”lådor”, som en första gissning låt de vara 10m x 20m stora. Det får plats 100 x 50 = 5000 sådana gräsplättar i skogen, men de kan innehålla träd. Notera dock att ett träd kan ”sabba” maximalt fyra områden, om trädcentrumet är precis i korsningen till exempel. Således kan 1200 träd sabba maximalt 4800 områden. Men då finns minst 200 osabbade områden. Fältbiologen kan välja och vraka!

Men hur ska man lösa problemet när det finns många fler träd? Vi nöjer oss med att lösa d), eller till och med för 4607 träd i skogen. Här nedan kommer Johans lösning.

Lösning:

Antag att det finns 4607 träd i skogen. Dela upp skogen i områden 10,5 m x 20,5 m på följande sätt:
Det får plats med 48 stycken långsidor på bredden och då är det 16 meter kvar också. På höjden finns det plats för 95 stycken kortsidor och då är det 2,5 meter kvar. Det betyder att vi kan få in några fler områden i remsan som är kvar till höger, nämligen 48 stycken. Totalt fås 48 x 95 + 48=4608 områden, alla med storlek 10,5 m x 20,5 m. Men det betyder ju inte att det finns områden utan träd, för ett träd kan stå på fler områden samtidigt.

Men det finns åtminstone ett område utan trädcentrum på grund av lådprincipen (det finns 4607 trädcentrum, men 4608 områden). Vi tittar närmare på detta område:

Om ett trädcentrum bara kan befinna sig utanför området, kan det bara ”intränga” på området med 25 cm. Den inträngningen sker från kanten. Alltså, om vi klipper bort 25 cm från varje sida, så är vi garanterade att ha trädfritt på det nya området. Vi ha klippt bort 0,5 meter på varje håll, så det området som är kvar är precis 20m x 10m, vilket var precis det som behövdes!

Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!

Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller tonårsben). Ju längre tid som går, desto mer måste man lära sig för att bli imponerad av något nytt tankesätt. Men som pris får man oftast upptäcka något ännu mer fascinerande än förra gången.

Ett av de här tillfälen var jag med om när jag för första gången besökte Uppsala. Det var någon gång vid årsskiftet 2001/2002 och jag gick i ettan på gymnasiet och kunde förstås inte så mycket om universitetsmatematik. Vilket i och för sig inte behövs för historien. Men snart får ni se hur allt ändå hänger ihop.

Vi fick sitta i ett klassrum och en matematiker berättade följade problem för oss.

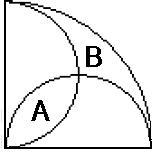
Tre olika cirklar ligger i planet och de skär inte varandra (och ligger inte inuti varandra heller). För varje par av cirklar dra två linjer, som tangerar båda två cirklarna. Om cirklarna är olika stora, kommer dessa två linjer att skära varandra. Frågan är nu: kommer de tre erhållna skärningspunkterna att ligga på samma linje?

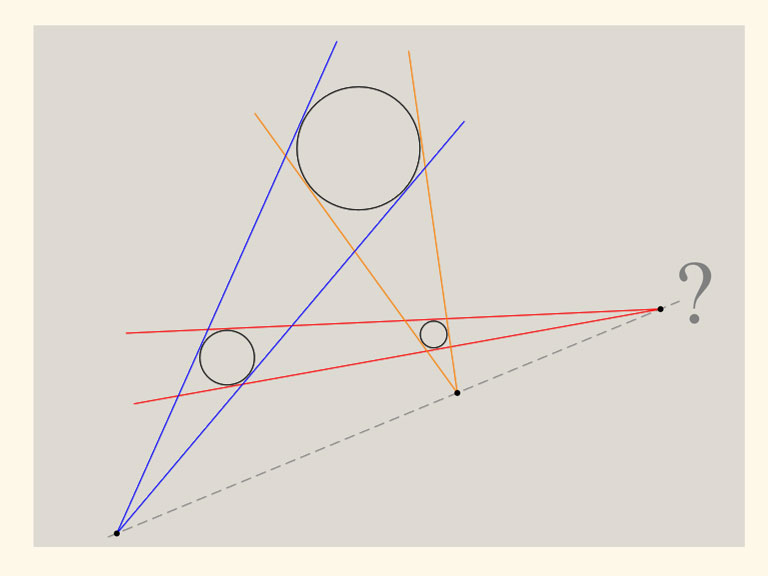
Det visar sig att de måste. Försök att lösa problemet med den geometrin du kan. Det verkar vara svårt att visa, genom att bara rita linjer och bestämma vinklar i planet.

Däremot finns en elegant lösning, som använder sig utav en tredje dimension!

Varför och hur?

Det är en väldigt imponerande idé, att gå högre upp än vad som verkar behövas. Om problemet inte kan lösas, så skall man försöka att titta på det ur en annan synvinkel. Men oftast ligger svårigheten i att välja rätt synvinkel.

Just att gå upp i högre dimensioner visade sig vara nyttigt även i andra vetenskaper. Mycket förklarades av insikten om att jorden är sfärisk, extra dimensioner behövs för att strängteorin skall hålla. Även min forskning handlar om att förstå enklare strukturer genom att titta på de mer kompilcerad. Men hur hjälper den tredje dimensionen i vårt problem?

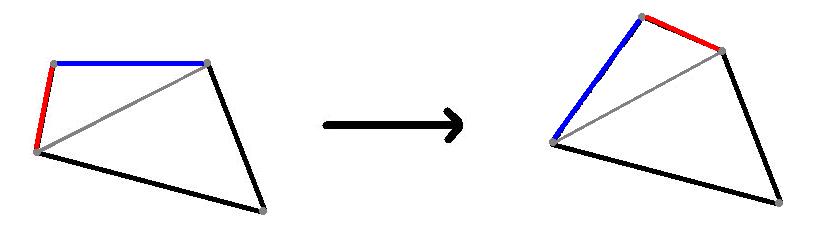
Föreställ er att det inte är cirklar, utan klot som ligger på ett plant papper, då ser det hela precis ut som på bilden om vi kollar uppifrån. Linjerna är fortfarande linjer, men i rymden kan vi faktiskt konstruera oändligt många linjer som är gemensamma tangenter till två av kloten. Alla dessa gemensamma tangenter bildar en kon, som har sin spets i papprets plan. Spetsen är då även skärningspunkten för de ursprungliga två linjerna.

Men om det finns tre kulor, så är det inte bara så att alla kan läggas på ett papper, vi kan lägga ett plant papper ovanpå dem också! Det pappret tangerar alla kloten, och det har lika mycket rätt att innehålla konspetsarna som det undre planet hade.

Således finns konspetsarna, det vill sägga de erhållna tre punkterna i båda planen. Och två plan skär varandra i en linje! Alltså ligger punkterna på en och samma linje.

Nu kan vi alltså glömma bort hela tredje dimensionen-grejen. Vi har visat att de tre punkterna ligger på samma linje i det tvådimensionella planet.

Här kan ni även titta på en film som illustrerar lösningen.

På ett område 1km x 1km växer en tallskog. Tallarna har alla diameter 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om det finns

a) 1200

b) 4200

c) 4500

d) 4600

träd i skogen.

Från början har vi en kvartscirkel med radie 1 (cm om man så vill). Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.

i) Hur förhåller sig areorna A och B?

ii) Vad är areorna A och B lika med?

Lösning:

(i) Notera att areorna A och C tillsammans utgör halva lilla cirkeln, det vill säga halva cirkeln med diameter 1. Den har area pi*((½)^2)/2. Samma gäller A och D, A+D=pi*((½)^2)/2=pi/8.

Å andra sidan utgör A+B+C+D en kvarts stor cirkel, således A+B+C+D=pi*(1^2)/4=pi/4. Vi ser att arean för den stora kvartscirkeln är dubbelt så stor som areorna för de små halvorna.

Således har vi A+B+C+D=(A+C)+(A+B), och subtraher vi A, B och C på båda sidor av likheten, så får vi A=B. Notera att vi nu inte har bestämt själva areorna, utan bara hur A och B förhåller sig.

(ii) Följande är min arbetskamrats Albins lösning:

Om man ritar ut den små (röda) cirklarna, syns det tydligare vad som händer. Den gröna punkten är skärningspunkten mellan tangentlinjer (svarta) till cirklarna, som då måste bilda 90° vid skärningen. Då är vinkeln mellan de två röda cirklarna också 90°.

Då vet vi att också de blåa tangentlinjerna skär varandra i vinkeln 90°. Det kan också ses av symmstriskäl. Från den gröna och från den blåa punktens perspektiv måste allting vara symmetriskt. Alltså bildas en kvadrat rektangel i mitten av bilden (en kvadrat egentligen), eftersom igen, av symmetriskäl så måste återstående två vinklarna vara lika och då måste de vara 90° också.

Nu finns olika sätt att bestämma arean A och jag gör det med liknande metod som i (i).

Här har vi att A+x=pi/16, en kvart av en cirkel med radie ½. A+x+x=1/4, arean av kvadraten. Alltså är x=1/4-pi/16. Och då måste A=pi/16-(1/4-pi/16)=pi/8-1/4.

Svar: 

Detta problem kommer från min arbetskamrat Albin. Eller, rättare sagt, punkten i) kommer från en gymnasiebok, men uppgiften missuppfattades och punkt ii) blev till, som är svårare.

Från början har vi en kvartscirkel med radie 1 (cm om man så vill). Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.
 

 i) Hur förhåller sig areorna A och B?

 ii) Vad är areorna A och B lika med?