Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om det enda som skiljer dem åt är ordningen på termerna.
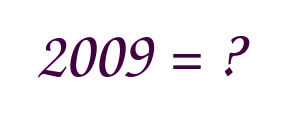
Diskussion:
Först och främst ska man pröva sig fram till lösningar, för att ”känna på” problemet. Det gäller alltså att komma på några sätt att dela 2009 i några nästan lika stora delar. En första tanke är att dela upp det som en summa av lika stora delar. Hur man göra det beror på vilka tal 2009 är delbart med.
2009 = 7*287 = 7*7*41
Så till exempel har vi uppdelningarna i exakt lika termer
2009 = 287 + 287 + 287 + 287 + 287 + 287 + 287
2009 = 1 + 1 + … + 1 (2009 stycken ettor)
2009 = 41 + 41 + … + 41 (49 stycken 41:or)
2009 = 2009
Men vad händer om vi försöker dela upp i ett visst antal termer, där antalet inte är en delare till 2009? Till exempel två termer? Då delar vi på två så gott det går, resultatet blir 1004 med rest. Men uppdelningen
2009 = 1004 + 1005
funkar ju, för att 1004 och 1005 är nästan lika.
Försök på samma sätt med tre termer. 2009 delat på 3 blir 669 och resten är 2. Då kan vi göra såhär:
2009 = 669 + 670 + 670
Den här idén med rester kommer vi att använda i lösningen.
Lösning:
Enligt villkoren måste varje sätt att summera upp till 2009 innehålla maximalt två sortes termer: ena kan uttryckas som x och andra som x+1. Ifall det fanns andra tal, skulle de inte vara nästan lika med x eller x+1.
Notera nu att för varje antal termer (beteckna antalet med n), så finns det ett sätt att dela upp 2009 i just så många nästan lika termer. Nämligen, dela 2009 med n med rest:
2009 = n*k + r
där k är kvoten och r är resten. Man vet att resten alltid är mindre än det man delade med, således mindre än antalet termer.
Likheten kan skrivas om:
2009 = k + k + … + k + r
där termen k förekommer n gånger. Men för att få just n stycken termer, fördelar vi r stycken ettor på r stycken k-termer. Det kan vi göra eftersom k är mindre än n. Således:
2009 = k + k + … + k + (k+1) + (k+1) + … + (k+1)
där termer av typen k förekommer (n-r) gånger och termer av typen (k+1) förekommer r gånger.
Så nu har vi 2009 stycken sätt att dela upp! Ett sätt för varje antal termer. Men finns det inga andra sätt?
Nej, faktiskt inte. Vi sa ju tidigare att termerna måste vara x och x+1. Har vi ett fixerat antal termer i summan
2009 = x + x + … + x + (x+1) + (x+1) + … + (x+1)
så kan vi inte ändra vare sig några x till x+1 eller tvärtom, för då skulle det hela inte summera upp till 2009.
Således är svaret: 2009 sätt.
