Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Former
Topologi handlar om olika slags former hos objekt. Båda barn och vuxna har bra intuition för former och hur de kan förändras, men ibland kan ointuitiva saker också hända:
Denna lektion skall vi experimentera med form hos olika sorts objekt med olika material.
Lera
När man ska förklara ordet topologi för någon som inte vet vad det är, så illustrera man ofta med detta exempel.
Man säger att en munk och en kopp är topologiskt sett samma, eftersom man kan omforma dem till varandra på ett naturligt sätt, om de nu skulle vara gjorda av modellera.

Lera är precis vad vi kommer pyssla med. Alla barn får var sin bit lera (t.ex. får alla var sin färg) och får i uppgift att tillverka en kopp med öra. Kan de göra det utan att riva leran någonstans? (Ńej, det kan de inte, så de får riva den här gången.) Kan de nu göra om koppen till en ring/en munk utan att riva leran? Det är tillåtet att klistra ihop leran, annars blir detta en väldigt opraktisk uppgift. I topologin får man egentligen inte klistra två punkter hur som helst om objektet ska behålla den topologiska formen.
Metalltråd
Även platta objekt kan vara topologiskt ekvivalenta eller inte. Till exempel kan siffrorna 1, 7 och 5 omformas till varandra, medan 9 och 6 tillhör en annan grupp. Skillnaderna är lättast att se om man tillverkar siffrorna i böjbart material, t.ex. snöre eller ståltråd och tydlig markerar platsen där materialet träffar sig självt igen (som i mitten på siffran 8).
Barnen får som första uppgift att på en bit ståltråd göra så många siffror den kan i rad. Början kommer att se ut ungefär så här:

Det viktiga är att tråden ska gå att räta ut igen!
Efter att barnen upptäcker att bara siffror 1,2,3,5 och 7 går att göra på det här sättet diskuterar vi hur det ligger till med andra siffror och sedan också bokstäver. Vilka stora bokstäver är till exempel i samma grupp som A?
(Svar: R)
Detta påminner om en gåta som folk länkar till då och då. Jag tror att det kan stämma att för mycket matematikutbildning skadar om man ska lösa gåtan fort:
8809 = 6
7111 = 0
2172 = 0
6666 = 4
1111 = 0
3213 = 0
7662 = 2
9312 = 1
0000 = 4
2222 = 0
3333 = 0
5555 = 0
8193 = 3
8096 = 5
7777 = 0
9999 = 4
7756 = 1
6855 = 3
9881 = 5
5531 = 0
2581 = ?
Knutar
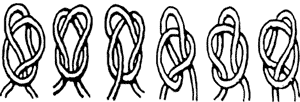
Barnen får två snören var för att experimentera med knutar. Först får de försöka knyta enligt schema, som denna knut:

Sedan gäller det att först gissa utifall bilden ger oss en knut eller inte utan att försöka göra knuten själv. Har man en gissning får man prova att bevisa det med hjälp av sitt snöre.
Flätor
Knutar är ganska enkelt för större barn, så de får gå vidare till flätor. Det finns förstås den vanliga flätan, som man gör med tredelat hår. Men det är inte bara den vi ska experimentera med.
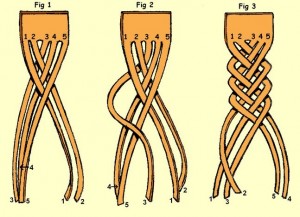
Även fyra delar kan ge en fläta:
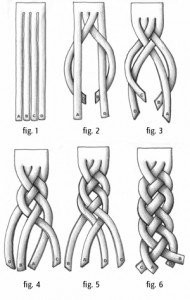
Och fem förstås:
Uppgifter utan ord
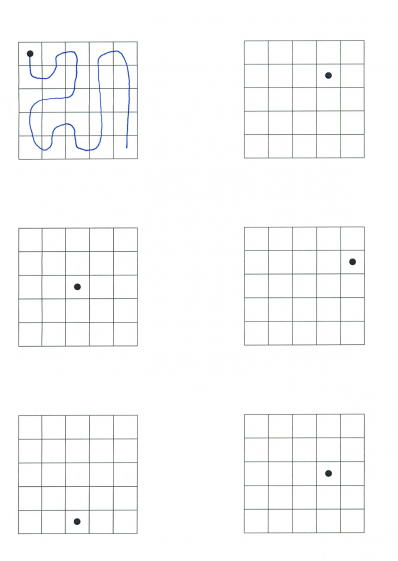
Jag är alltid mycket för den visuella matematiken. En bild säger verkligen mer än tusen ord. Uppgiften nedan som vi avslutar med (den har inte så mycket med topologi att göra) kommer ursprungligen från inläggetMath without Words.

Det ser ut som en väldigt spännande lektion (förutom att det känns fel att ha en topologilektion för barn utan möbiusband att klippa och klistra med :) ).
Att ha mer matematikutbildning är kanske också bra till problemet, om man vet vad Bettital är så går det fort :)
Jag tycker fortfarande att knutar är komplicerade nog att tänka mer på (då jag inte är ett stort barn nog för att det ska kännas lätt) så jag har inte tittat så mycket på flätor, men en ganska trevlig fråga är om man till varje fläta kan skapa en ”antifläta”, dvs kan man skapa för en given fläta hitta en annan fläta att koppla ihop den med så att resultatet bara är (efter omformning) raka ”hårstrån”.
Ett par andra trevliga saker man kan göra är att sätta ihop ändarna på knuten du har på din bild. Då får man en såkallad figur-åtta knut. En övning kan vara att visa att en sådan knut kan omformas till sin egen spegelbild (alla knutar har inte denna egenskap).
Om man tröttnar på de låga dimensionerna på sina objekt så kan man titta på ytor istället som i filmen i början. Det finns ett till liknande problem med en genus-2 yta som ”länkar” sig själv (tror den finns på framsidan till ”basic topology” av armstrong) istället för med ett annat objekt som man sedan ska visa kan ”avlänkas”.
Ett tredje trevligt problem är följande: Om man sticker hål på en badboll så kan man vända den ut och in. Kan man göra samma sak om man sticker hål på en badring?
Jag höll för ett par år sedan ett populärvetenskapligt föredrag om matematik/topologi som jag avslutade med handklovsproblemet (http://mathssquad.questacon.edu.au/the_handcuffs_puzzle.html har en trevlig beskrivning +animation av lösning) för alla som lyssnade. Det är ganska roligt att se folk försöka trixa sig ur det och problemet har en topologisk poäng + att det tvingar folk att samarbeta även om det kanske inte passar de absolut yngsta.
Vad är uppgiften på de sista bilderna? Att ta sig från punkten runt till alla kvadrater utan att besöka varje kvadrat mer än en gång (om/när det går)?
Jag uteslöt medvetet laborationen med möbiusband. Några föräldrar berättade om försöka att visa olika experiment för sina barn, som fick måla och klippa, men barnen var tydligen inte imponerade. Det kan vara så att 5-7-åringar fortfarande är för unga för att se det häftiga. Man ska nog bli van med vanliga ringar och ytor innan de ovanliga introduceras.
Både knutor och flätor var dock avancerat för barnen! Långt ifrån alla lyckades göra en egen knut som det såg ut på bilden. Kanske var inte bilderna tillräckligt tydliga, kanske var det bara ovana. De kunde iofs se när det skulle bli en knut och när det inte skulle bli det. Så det där med antifläta känns överkurs. Men intressant tips i vilket fall!
Vi hann inte hålla på med lera förra lektionen, så 3D-uppgifter kommer jag ta nu på söndag. Vad gäller torusar tänkte jag föreslå det klassiska ”3 hus, 3 personer”-problemet, dvs rita ”planärt” (först på papper, sedan på torus, hur jag nu ska få tag på torusar).
”planärt” (först på papper, sedan på torus, hur jag nu ska få tag på torusar).
Handklovproblemet låter kul, jag har letat efter den faktiskt! (Visst körde du den på Sonja Kovalevsky-dagarna?) Kanske kan mina 10-åringar komma på lösningen efter några tips.
Yes, och man får inte gå diagonalt. Uppgifter är precis som man tror att det är. För övrigt tycker de sjuåriga barnen mycket om sådana pussel.
Det kanske stämmer att man behöver mer erfarenhet innan man ser det häftiga (även om jag skulle vara lockad att ge någon ett möbiusband och be dem måla en sida blå och en sida röd och se vad som händer). Tror du det skulle fungera bättre med 10-åringarna?
Det finns ett väldigt vackert bevis på att det alltid går att konstruera en antifläta. Håll flätan ovanför klart, blankt vatten så att ändarna precis vidrör vattnet. Då ser du en spegelbild av flätan i vattnet. Detta är antiflätan. Man kan se hur den ”löser upp” den ursprungliga flätan genom att långsamt sänka ned den i vattnet.
Det går givetvis också att observera att flätan/flätgruppen generas av korsningar och använda att de är inverterbara (på ett mer eller mindre formellt sätt), men jag gillar vattenbeviset.
Handklovsproblemet är precis det jag använde på SK-dagarna :) Problemet är nog inte så beroende av matematisk vana (jag lyckades få matematikdoktorander/masterstudenter att sitta ihop väldigt länge, medans vissa gymnasieelever kom på det efter 2-3 minuter). På sidan jag refererade till så hade de ett par trevliga tips på hur man kan hjälpa till utan att avslöja hela lösningen. Det kan vara bra att göra handklovarna stora så att det är uppenbart att det finns ledigt utrymme mellan handled och handklov.
Tittade du någonsin på http://www.geometrygames.org? Det finns ett spel där som man kan använda för att introducera torusar (utifrån den planära beskrivningen som R^2 kvotat med Z^2) som kanske sjuåringarna skulle uppskatta om de gillar spel/pussel. Jag tror de flesta går att överföra till papper utan större problem sålänge man indikerar att när man går ut till höger så kommer man tillbaka till vänster osv.
Jo, möbiusbandexperiment tror jag har minst 9-10 år som lämplig ålder. Handklovarna har de dock svårt med, även efter tips. Men kul hade de i processen i alla fall!
Mm, vattenbeviset har du berättat för mig förut, men det är inte riktigt så att man kommer på det själv. Men det skulle kunna gå att exprimentera med snören som du sade förut.
Har tittat lite på geometrygames, framför allt mönsterprogrammet. Men det är lite svårt för mig att arbeta med det, eftersom min dator bara har Linux. Vad går torusspelen ut på?
det finns flera stycken torusspel, (ca 10 st tror jag). Alla spelen utspelar sig på en torus, som representeras av en kvadrat med identifierade sidor. Man kan flytta runt var på torusen man har kvadraten centrerad. Det finns ett par varianter på 3 i rad/5 i rad, billiard, en schackvariant, ett pussel, minröjarspel, och en labyrint där man ska hjälpa en råtta att hitta ost + ett par till som bygger på att man kan engelska. Råttspelet är nog det somk passar flest personer eftersom speliden är uppenbar och det enda man måste hålla reda på är att om man går ut på ena sidan så kommer man in på den andra. Det går också att spela på en kleinflaska om man vill förvirra folk mer.
Curved spaces ”spelet” på samma sida är också ganska fascinerande, man får undersöka olika 3-dimensionella topologiska rum genom att flyga genom dom. Vackert och förvirrande, precis som topologi kan vara :)