Du har 127 enkronorsmynt och 7 tomma plånböcker, och du måste lägga in alla mynten i plånböckerna. Om någon ber dig om
en summa pengar, skall du kunna ge dem några plånböcker, så att det tillsammans i dem finns precis så många kronor som det frågades efter. Hur skall du fördela mynten mellan plånböckerna på så sätt att du kan ge ut vilken summa under 128 kronor som helst utan att öppna dem, om någon ber om det?
Eftersom vi kommer att behöva kunna dela ut exakt 1 krona, måste vi även ha en plånbok med exakt 1 krona i, det går ju inte att dela upp beloppet på flera plånböcker.
För att kunna dela ut 2 kronor, lägger vi i 2 kronor i den andra plånboken. Nu kan vi dela ut både 1, 2 och 3 kronor (3 kronor delas ut genom att man ge bort båda plånböckerna).
I den tredje plånboken lägger vi 4 kronor. Nu kan vi dela ut 1,2,3 kronor som förut, samt dela ut plånböcker som förut, men tillsammans med 4 kronor-plånboken: detta ger summor på 1+4,2+4 och 3+4 kronor. Vi kan också dela ut plåboken ensam, vilket ger beloppet 4 kronor. Totalt kan vi dela ut 1,2,3,4,5,6 eller 7 kronor.
Fortsätt på samma sätt: fjärde plånboken får 8 kronor, femte får 16 kronor, sjätte får 32 kronor och sjunde får 64 kronor i sig (antalet kronor i nästa plånbok är alltid lika med nästa tvåpotens). Varför går det att dela ut alla belopp under 128 kronor?
Ett sätt att motivera det är att vårt belopp antingen är större än eller lika med 64 kronor, eller mindre. I det första fallet kommer vi att ge bort plånboken med 64 kronor, i det andra lägger vi undan den för den kommer inte att användas.
Resten av beloppen som ska delas ut är antingen större än eller lika med 32 eller mindre än 32. Dessutom är vi säkra på att det är mindre än 64 kronor (ty sammanlagt var det från början mindre än 128). I det första fallet kommer vi att ge bort plånboken med 32 kronor och i det andra lägga undan den plånboken, för den kommer inte att användas.
Fortsätt på samma sätt att avgöra huruvida vi skall använda nästa (mindre) plånbok eller inte. I det sista steget kommer vi antingen att ha 1 krona eller 0 kronor kvar att dela ut. Antingen ger vi bort plånboken med 1 krona i då, eller så låter vi bli det.
Det strikta beviset för varför detta fungerar är följande:
Från början hade vi mindre än 
mynt. Vid varje steg har vi mindre än 
mynt att passa ihop med plånböcker och vi har plånböckerna med värden 
,
, 
, …
.
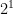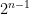Om antalet mynt vi har kvar att dela ut är mindre än 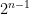, så går vi till nästa steg: nu betraktar vi plånböcker med värden ,, , …
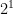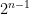och mindre än kronor att dela ut.
Om antalet mynt vi har kvar att dela ut är större än 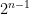, så ger vi bort plånboken med 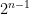mynt i. Då har vi kvar mindre än 
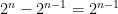kronor att dela ut. Och vi har plånböckerna med värden ,,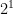 , … återigen.
I båda fallen reducerade vi n med 1 och kom till en motsvarande situation. Då n=0 blir vi klara, för då har vi kvar mindre än 1 krona att dela ut, det vill säga 0.
Ett annat problem i samma härad som jag gillar:
En kung ska bjuda till gästabud om en månad. Han har fått reda på att en av hans tusen flaskor vin innehåller ett oerhört dödligt gift (ospårbart, några molekyler räcker för att döda) som verkar först efter fyra veckor.Han vill inte döda en slumpmässig undersåte genom att låta tusen stycken smaka, men kan tänka sig att offra sina tio dödsdömda fångar.
Hur kan kungen hitta den förgiftade flaskan i tid till gästabudet?
Ja, det är ett jättesnyggt problem! Jag och en kompis håller på att skriva en bok om 40 snygga problem, och ”Det förgiftade vinet” är ett av dem :)
Du råkar inte veta var du först såg problemet?
Det går att ställa ett villkor för att 2^n-1 ska kunna vara ett primtal. Det bygger på den ganska enkla polynomfaktoriseringen x^m-1=(x-1)(x^(m-1)+x^(m-2)+…+x+1),
Ifall vi antar att n inte är ett primtal så kan den skrivas på formen n=ab där både a och b är större än 1. Låt 2^a=x och b=m i vår formel så får vi att
2^n-1=(2^a-1)((2^a)^(m-1)+(2^a)^(m-2)+…+(2^a)+1), Då a,b båda var större än 1 så har vi nu faktoriserat 2^n-1 i två faktorer som är större än 1. Alltså så
r inte 2^n-1 ett primtal om inte n är ett primtal (vilket gör det lätt att generera motexempel). Primtal på denna form kallas Mersenneprimtal.
Tyvärr så är inte alla tal på formen 2^p primtal, det finns motexempel redan på ganska låga primtal.
Det går att ställa ett villkor för att 2^n-1 ska kunna vara ett primtal. Det bygger på den ganska enkla polynomfaktoriseringen x^m-1=(x-1)(x^(m-1)+x^(m-2)+…+x+1),
Ifall vi antar att n inte är ett primtal så kan den skrivas på formen n=ab där både a och b är större än 1. Låt 2^a=x och b=m i vår formel så får vi att
2^n-1=(2^a-1)((2^a)^(m-1)+(2^a)^(m-2)+…+(2^a)+1), Då a,b båda var större än 1 så har vi nu faktoriserat 2^n-1 i två faktorer som är större än 1. Alltså så
r inte 2^n-1 ett primtal om inte n är ett primtal (vilket gör det lätt att generera motexempel). Primtal på denna form kallas Mersenneprimtal.
Tyvärr så är inte alla tal på formen 2^p-1 primtal, det finns motexempel redan på ganska låga primtal.