Phi-växter, pi-växter och e-växter, del 2

I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.

Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144 graders mellanrum. Det innebär att nya blad sprutar ut 144, 288, 432 (det vill säga 72), 216 graders mellanrum i förhållande till det första. Men nästa blad, det sjätte, kommer hamna 360 grader ifrån det första, det vill säga på exakt samma ställe! Detta är väldigt ooptimalt för en växt.

Oavsett vad för rationellt tal vi tar kommer samma elände att hända efter p blad, eftersom då har bladen avlagt 360/(p/q)*p = q*360 grader, alltså ett helt antal varv. Växten vill att det aldrig riktigt ska bli helt.

Så händer det inte med de irrationella talen. Låt oss jämföra vad vi får för irrationella växter. I tabellen ser du en rationell växt, en phi-växt, en pi-växt och en e-växt. Början ser det relativt likt ut emellan alla växterna:

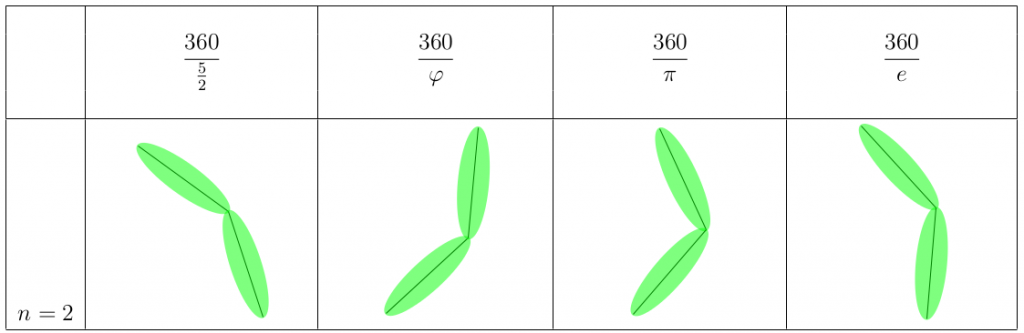
Men efter fem blad har den första växten fördelat sina blad jämnt, medan de andra ser annorlunda ut. Phi-växten har fördelat sina blad ganska bra, medan pi-växten har sina blad onödigt trångt.

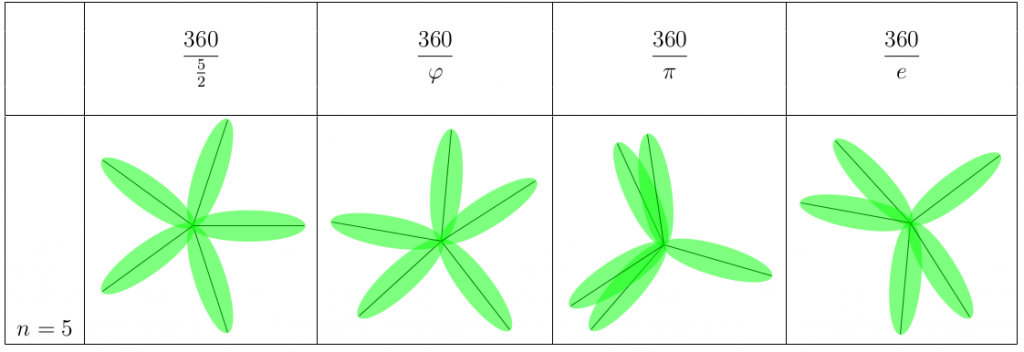
Vad händer vid 12 blad? Oförändrat för den rationella växten – den kan bara ha sina blad på 5 positioner. Phi-växten är jämnfördelad som vanligt, e-växten är också ganska bra. Pi-växten har däremot tre tydliga delar. Kan det ha att göra med att pi på ett ungefär är lika med 3?

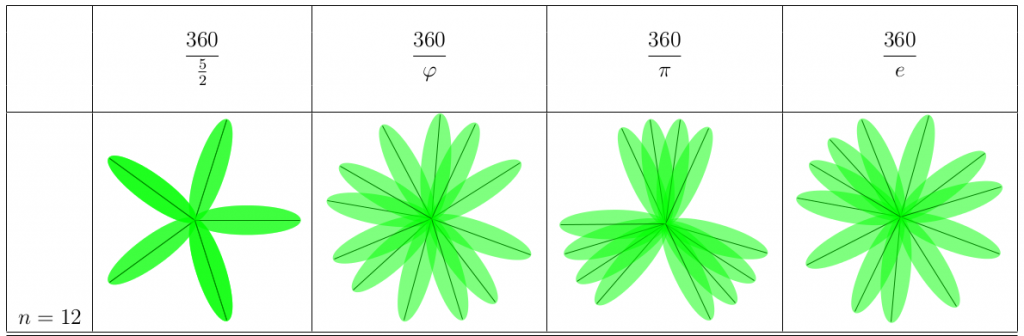
Vi 30 ser vi hur växterna klarar av många blad. De mörkare partierna visar på att bladen överlappar varandra, vilket sker mer och mer på e-växten och pi-växten speciellt. Överlappningen finns hos phi-växten också, men den är mer jämnfördelad. Notera att pi-växten har 22 tydliga delar!

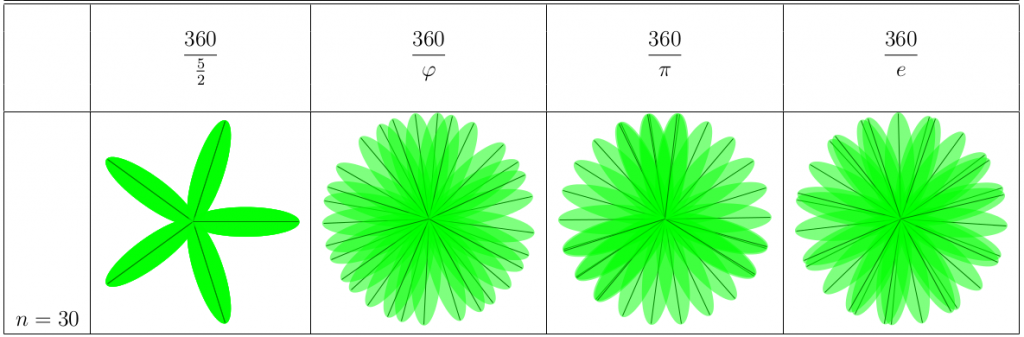
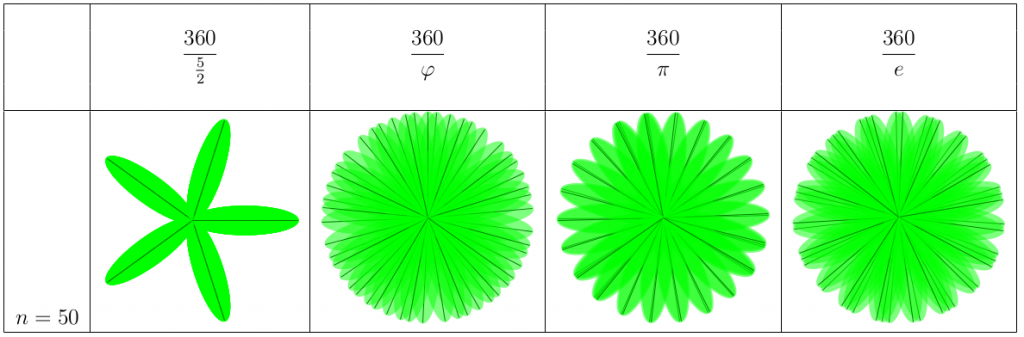
Till sist kollar vi riktigt många blad, 50. Pi-växten har 22 väldigt tydliga delar, e-växten har 19, medan phi-växten aldrig har två blad så pass nära varandra som de andra växterna. Den verkar ha 5 stora delar, vilket tyder på att vi i verkligheten skulle se 5 spiraler för den bladstorleken.

Varför blir det 22 tydliga delar hos pi-växten? Det har att göra med att pi approximeras väldigt bra med talet 22/7 (ca 3,14), vilket får växten att agera som en vanlig rationell växt och överlappa sina egna blad efter 22 stycken. Varför är vissa växter ändå pi-växter, som vi såg i förra delen? Jag gissar på att många verkliga plantor inte har så många blad eller grenar, och därför spelar det inte så stor roll för dem att det blir problem efter 22 stycken. De satsar snarare på 3 eller något sådant.

På samma sätt är 19/7 ett rationellt tal nära talet e (men inte lika när som 22/7 är pi), därför bildas det 19 delar på e-växter. Jag vet inte varför jag inte träffat på e-växter hittills, de verkar ju växa helt ok i början.

Men talet phi är väldigt speciellt. Det finns inte någon rationell approximation av det talet som är i någon mening så bra som 22/7 är för pi. Visst, vi kan använda större nämnare för att få ett rationellt bråk som är så nära phi som vi vill, men då blir nämnarna nästan onaturligt stora. För mer rigorös definition av bra rationella approximationer, se Hurwitz sats. Konstanten i satsen kommer just ifrån phi, det gyllene snittet, och det är det som medför att phi är det mest irrationella talet.

Det innebär att just den konstanten är optimal för växter med stort antal blad, frön, grenar etc. och det är därför vi vanligen finner just 34 och 55 spiraler på solrosor och inte 22 (Klicka på bilden för att räkna själv).