Rekommenderad från: 15 år
Du sitter i en fängelsehåla och en vakt kommer till dig med ett erbjudande. Han säger att han kommer lägga upp mynt (totalt 64 st.) på ett schackbräde, ett mynt i varje ruta och det kommer vara slumpat för varje mynt huruvida det ligger med krona eller klave uppåt. Därefter kommer vakten peka på en ruta. Du får sedan en möjlighet att vända upp-och-ner på exakt ett av mynten, vilket du vill.
Därefter kommer en kompis in i rummet, som får se schackbrädet och får gissa vilken ruta vakten pekade på. Gissar han rätt, får ni båda gå fria. Hur kan du och kompisen komma överens om en strategi som garanterar er frihet, oavsett hur vakten gör?

För enkelhets skull betecknar vi myntet med 1 om det ligger med krona uppåt och med 0 om det ligger med klave uppåt.
Lösning 1 (Krånglig, men Valentinas egna)
Lösningen visar att det går att konstruera en sådan strategi (och hur man konstruerar), men det är inte självklart hur man ska implementera det direkt. Lösningen använder sig av matematisk induktion.
Först löser vi uppgiften då antalet mynt är två (schackbrädet är tvårutigt). Då kan mynten ligga på fyra sätt från början: 00, 01, 10 eller 11. Vi bestämmer att vi gör om bräder till 0* (det vill säga 00 eller 01) om vakten pekar på det vänstra myntet och till 1* (det vill säga 10 eller 11) om vakten pekar på det högra myntet. Vi kan ju alltid vända vänstra myntet om det visar ”fel” eller vända högra myntet om det vänstra visar ”rätt” redan.
Nu gör vi induktionsövergången från n mynt till 2n mynt. Induktionssteget är alltid likadant, så för förståelsen skull gör jag en konkret övergång från 32 till 64 mynt.
Antag alltså att vi har löst problemet för 32 mynt. Det betyder att vi i varje situation kan vända på ett av mynten så att kompisen förstår vilket av de 32 mynten vakten pekade på genom att bara titta på slutpositionen. Vi antar även att varje slutposition (av 2^32) i sin tur betyder att en viss speciell ruta blev pekad på. Så är ju fallet för 2 mynt. Det betyder att vi från varje startposition på 32 mynt kan göra om brädet så att slututseende har ett visst ”värde” (från 1 till 32).
Antag att vakten pekar på ett mynt med ett nummer som ger rest r vid division med 32. Till exempel, om resten är 3 så pekade vakten på mynt nummer 3 eller nummer 35. Då kan vi ändra brädet på två möjliga sätt så att summan av numren som de två halvorna betyder (i 32-systemet) också ger rest r vid division med 32. Det beror på att vi kan fixa vilken rest vi vill i en av halvorna enligt induktionsantagandet. På så vis kan kompisen (som även kan systemet för 32 mynt) lista ut att myntet vakten pekade på var nummer 3 eller 35 (genom att räkna ”summan” av brädhalvornas värden). Men hur ska hen avgöra vilket av de två alternativen gäller i 64-systemet?
För detta använder vi lösningen för 2 mynt. Vi kan räkna antalet kronor (uppåt) i varje brädhalva. Är det ett jämnt antal i båda halvorna betecknar vi brädet 00. Är det jämnt antal kronor i första halvan och ett udda antal i andra, så betecknar vi brädet 01 och så vidare.
Genom att vända upp-och-ner på ett av mynten kommer vi garanterat förändra en av siffrorna. Låt oss då bestämma att vi vänder så att det blir 00 eller 01 (vi kan bestämma i vilken halva vi vänder) utifall kompisen ska säga det lägre alternativet (3 i vårt exempel) och vi vänder så att det blir 10 eller 11 ifall kompisen ska säga det högre alternativet (35 i vårt exempel). Detta kan vi alltid på samma sätt som i lösningen för två rutor!
Det betyder att kompisen kan med säkerhet bestämma vilket mynt som vakten pekade på.
Lösning 2 (Snygg och praktisk, min vän Mikkes lösning)
Här är instruktionerna för hur kompisen listar ut vilket mynt vakten pekade på:
Först kollar du om det finns ett udda antal 1:or (dvs kronor uppåt) i det gröna området. Om det gör det — då letar du efter rutan i det gröna området, annars (om antalet 1:or är jämnt i det gröna) letar du efter rutan i det vita området. Lägg det stora området på minnet.
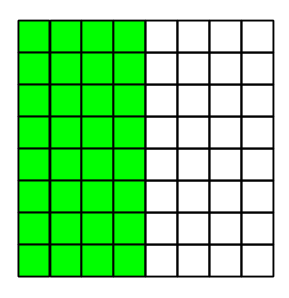
Nu kollar du om det finns ett udda antal 1:or (dvs kronor uppåt) i det nya gröna området. Om det gör det — då letar du efter rutan i det gröna området, annars letar du efter rutan i det vita området. Lägg det andra stora området på minnet (redan nu vet du i vilken ”fjärdedel” myntet bör ligga).
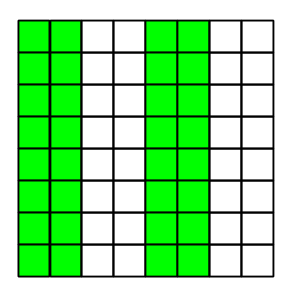
Gör på samma sätt med resterande gröna områden:
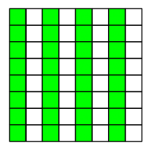
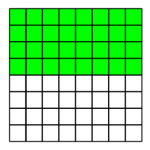
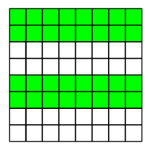
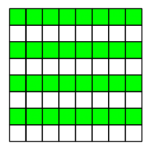
För varje nytt halvgrönt bräde (som du föreställer dig i huvudet) halverar du antalet möjliga svar. Efter sex bräden har du kommit fram ett enda möjliga myntet och det kommer vara myntet som vakten pekade på!
Varför är det då möjligt för dig att fixa myntvädningen så att kompisen kan lista ut det utpekade myntet? Du kan också föreställa dig de halvgröna bräden en i taget och se ifall kompisen kommer komma rätt. Är det så att det utpekade myntet ligger i det gröna området? Då ska du fixa så att det ligger ett udda antal 1:or i det gröna området. Antingen genom att vända i den vita halvan ifall det redan är udda i grönt eller vända i den gröna halvan ifall det är jämnt antal 1:or i grönt. Är det så att det utpekade myntet ligger i det vita området? Då fixar du så att det är ett jämnt antal 1:or i den gröna halvan.
Det här liknar alltså sista biten i Lösning 1.
På samma sätt gör du med de andra fem halvgröna bräden. Detta ger dig exakt ett bestämt mynt som du måste vända på för att fixa de korrekta pariteterna (jämn/udda precis där det behövs)!
Lösning 3 (För datavetare)
Detta är detsamma som Lösning 2, men på datorspråk. Varje myntnummer är ett binärt tal mellan 000000 och 111111 (6 bitar). Skriv upp alla tal vars mynt har krona uppåt. Gör operationen XOR på alla de mynten (med andra ord, kolla pariteten på antalet 1:or på varje bit). Gör XOR på det resultatet och numret på myntet som vakten pekade på. Detta ger numret på myntet som du ska vända på!
Din kompis listar ut resultat på samma sätt, genom att XOR:a alla ettor (kronor uppåt) som hen ser.
Dela inlägget:
- Klicka för att dela på Facebook (Öppnas i ett nytt fönster) Facebook
- Klicka för att dela på X (Öppnas i ett nytt fönster) X
- Klicka för att dela på Reddit (Öppnas i ett nytt fönster) Reddit
- Klicka för att e-posta en länk till en vän (Öppnas i ett nytt fönster) E-post
- Klicka för utskrift (Öppnas i ett nytt fönster) Skriv ut

Vad händer om schackbrädets sida/sidor inte är en 2-potens? Kan man fortfarande lösa problemet?
Hej! Vad jag ser så är det inte möjligt. Oavsett storleken på brädet har vi precis så många alternativ till vändning så att det räcker att särskilja på mynten, det vill säga vi kan inte slösa med information. På grund av symmetri borde lika många utseenden på brädet (dvs upplägg av mynt) ha samma värde för varje värde. Men antalet utseenden på brädet är en tvåpotens, medan antalet värden är inte det, motsägelse.
Hmm, inte helt säker på att jag hänger med på ditt argument.
På det rätt enkla fallet då vi har ett 3×1 bräde (1×1 är ju en tvåpotens…) så går det att lösa, min regel är helt enkelt att den som det bara finns en av är den vi väljer (med exempelvis XOX väljer vi mitten och med OOX den till höger). Detta går att konstruera oberoende av startsituation.
Vet inte
I fallet 1×3 går det t.ex. inte att fixa ifall det ser ut som XOX från början och vakten pekar på mittenmyntet, eftersom man måste vända på något.
Mitt resonemang tillämpat på 1×3-fallet: Det finns 8 lägen som brädet kan vara i. Det betyder att någon myntposition ska klara sig med högst två lägen. Det vill säga hur vi än har mynten från början ska vi kunna komma till de två lägen. Eftersom grafen över lägen (och övergångar dem emellan) är symmetrisk kan vi välja två lägen åt alla andra mynt också, som kan nås var som helst ifrån (det steget är jag inte helt säker på, men känns intuitivt att det stämmer). Då behöver vi bara 6 lägen. Det betyder att vi någonstans förlorar information, vilket vi inte har råd att göra.
”Du får sedan en möjlighet att vända upp-och-ner på exakt ett av mynten, om du vill. ” Tolkade jag som att det var frivilligt att vända på mynt.
Om det inte är frivilligt så håller jag jag nog med.
Det enda intressanta är antalet rutor (så MNx1=MxN rutor), jag antar N rutor.
Vi kan se en given position (utdelade krona/klave) som en nod i hyperkubsgrafen K={0,1}^N. Vi vill då hitta N disjunkta nodmängder X_i så att varje sådan mängd X_i har egenskapen att för varje given nod g så finns det en granne till g i X_i (dvs genom att ”flippa” ett mynt kan vi hitta till en konfiguration som bestämmer rutan i).
Vi noterar också att varje nod har precis N grannar, så varje granne måste tillhöra någon X_i, alltså måste vi fylla upp vår graf helt (då varje nod måste tillhöra något X_i). Dvs den disjunkta unionen av alla våra X_i är K. Antag att vi har hittat en sådan konfiguration av mängder. Vi ser också att varje nod har precis 1 granne i varje X_i.
Låt oss ta en sådan mängd X. Vi summerar antalet grannar tillhörande X över varje nod i hyperkuben. Detta blir trivialt 2^N (då varje nod hade exakt en sådan granne). Vi kan också räkna ut summan genom att ta varje nod i X och summera antal grannar den har. Detta blir då |X|*N (då varje nod har exakt N grannar, så speciellt har varje nod i X det). Alltså så har vi |X|*N=2^N.
Då följer att N|2^N!
Ja, så kan man också göra! Det blev ju nästan lite ”Lagrange sats”-känsla över beviset :)
Du har rätt, jag publicerade en gammal formulering av problemet, ska ändra på det. Först var jag nämligen osäker på om man var tvungen att ändra, men sedan utgick jag från att man var tvungen (tänkte att man ändå inte tjänade så mycket på att inte vara tvungen att vända). Men i den svagare versionen vet jag inte vilka N som lösningen existerar för. Skulle gissa att det går för 3, men inte för 5 eller högre.