Det här roliga problemet har jag fått av min kompis Fredrik från Genikampen-2015!
Rekommenderad från: 15 år
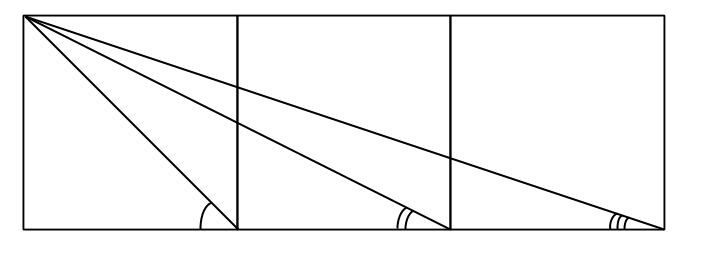
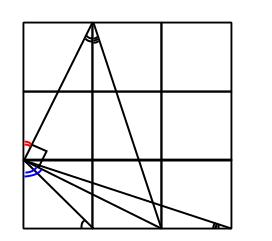
Tre kvadrater är ritade bredvid varandra. Tre linjer dras från ett hörn som bilden visar. Bestäm summan av de tre utsatta vinklarna (i exakt antal grader eller radianer):
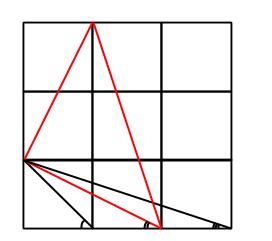
En av möjliga lösningar lyder så här. Vi ritar några rutor till och markerar en röd triangel på följande sätt:
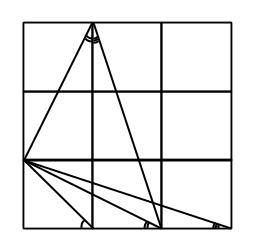
Nu vill vi bevisa att triangeln är lekbent och rätvinklig, det vill säga en 90-45-45-triangel.
Varför vill vi det? Jo, notera att ena hörnet består av två vinklar: en tvåa och en trea, det vill säga två av de minsta vinklarna som problemet handlar om.
Detta stämmer, eftersom vinkelns ena del ingår i en rätvinklig triangel med kateterna 1 och 2, medan vinkelns andra del ingår i en rätvinklig triangel med kateterna 1 och 3. Det är precis sådana rätvinkliga trianglar som innehåller de ursprungliga tvåan och trean.
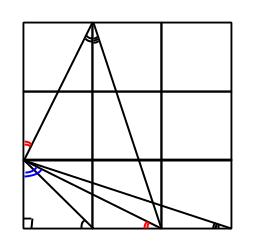
Vi kan även hitta en till rätvinklig triangel med kateterna 1 och 2, som då innehåller en tvåa (den nya röda vinkeln på bilden). Den blå vinkeln är den som tillsammans med en röd ger 90 grader, eftersom de är just de två spetsiga vinklarna i triangeln med den ursprungliga tvåan.
Det betyder att även vinkeln mellan den nya röda och den blå vinkeln också är 90 grader, eftersom alla de tre tillsammans ska ge 180 grader.
Men den stora röda triangeln är även likbent, eftersom de röda kateterna i själva verket hypotenusorna i de små trianglarna med kateterna 1 och 2, och dessa hypotenusor måste vara lika!
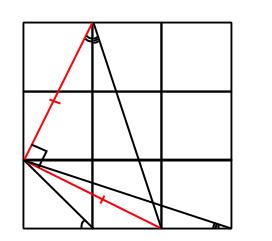
Men om den stora röda triangeln har vinklarna 90-45-45 betyder att summan av tvåan och trean är 45 grader. Ettan är lika med 45 grader, ty den ingår i en liten 90-45-45-triangel från början. Alltså är summan av de tre angivna vinklarna lika med 90 grader!
Notera att vi inte bestämde vad varje vinkel var lika med (bara ettan), men vi vet ändå att summan av de alla är 90 grader.
Man kan även lösa problemet på flera andra sätt, se kommentarerna till inlägget.
Dela inlägget:
- Klicka för att dela på Facebook (Öppnas i ett nytt fönster) Facebook
- Klicka för att dela på X (Öppnas i ett nytt fönster) X
- Klicka för att dela på Reddit (Öppnas i ett nytt fönster) Reddit
- Klicka för att e-posta en länk till en vän (Öppnas i ett nytt fönster) E-post
- Klicka för utskrift (Öppnas i ett nytt fönster) Skriv ut

45/22,5/15
Summan av de tre vinklarna är 90 grader. tan ( =1, tan (( = 1/2 och tan ((( = 1/3. Fördubblar man figuren och ritar lämpliga trianglar kan man visa att (( + ((( = 45 grader.
Jag fick 45/27/18. Stämmer det?
45/30/15
Jag tror inte att alla dessa vinklar kan uttryckas i ett rationellt antal grader. Men i uppgiften behöver ni hitta summan och då behöver man inte hitta de enskilda vinklarna.
Hej Val! A=45 grader, tan B = 1/2 och tan C = 1/3 .Tan(B+C)=(5/6)/(1-1/6)=1 så (B+C) = 45 grader och därför får man att (A+B+C) = 90 grader. En annan lösning/bevis som du kan lägga ut har jag skickat som mail till dig och några kända problemlösare. Tyvärr får detta problem inte många kommentarer i gruppen Matematikundervisning på Facebook.
Ah, coolt, Sture! Jag kunde inte formeln för tangens summa. Själv löste jag med likformighet, men den snygga lösningen är via en likbent triangel, som jag kommer lägga upp senare. Såg att du startade en diskussion på Matematikundervisningsgruppen, kul att det fanns en hel video om problemet!
Man kan också använda Diofantos metod för att med hjälp av två rätvinkliga trianglar ta fram en större rätvinklig triangel. Han gjorde precis som vi gör när vi multiplicerar ihop komplexa tal. Här har vi binomem
(2+i) och (3+i) och multiplicerar ihop dem. i*i=-1. (2+i)*(3+i)=6+3i+2i + i*i=6+5i-1=5+5i som kan ses som en rätvinklig triangel där kateterna är 5 och hypotenusan är sqrt(50) , dvs en halv kvadrat
90+45+30=165grad
90 degrees, see http://tinyurl.com/oun7bjf
Very elegant problem :)
If we number the squares (starting from the left) whose corners the straight lines extend to (the ones to build angles from), we can define this problem as 1,2,3
Extending the idea of adding more than three squares in a row and drawing lines from the upper left corner, we can get new problems with the same solution with more lines.
For example with four angles:
1,2,5,8
1,2,4,13
Hur hittar man tan 45/2? Jag fick att tan 45/2 =(sqrt(2)-1)
There are a lot of good ways to find tan(45/2)
One easy way would be to use the half angle formulas for sine and cosine and go back to the definition of tan as sin/cos. Then you have a formula with sin(45) and cos(45) to simplify.
There are other methods as well.
Denis, your solution is really beautiful!
DMT, thanks for the generalisation ideas!
Mer om summan av olika arctan: https://www.maa.org/…/files/Fibonacci_Numbers55908.pdf