Rekommenderad från: 10 år
[kkratings]
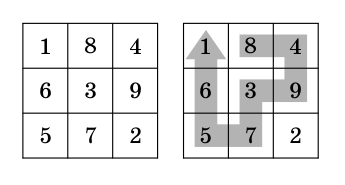
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.
Katarina gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).
Mattekorsord 2011
Jag behåller traditionen och presenterar ett sifferkorsord även i år. Denna är lite svårare än förra året, men också lite mindre. Utmana dina nära och kära eller lös korstalet tillsammans.
God Jul önskar mattebloggen!
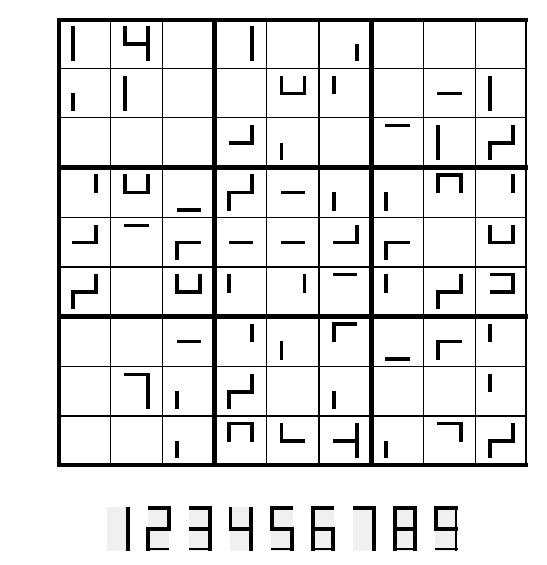
Mattekorsord 2011
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.
Vågrätt:
1. Fibonaccital
3. Delbart med 11
6. Summan av talen från 1 till 1000
7. Närmaste heltalet till
9. Ett tal vars siffersumma delar sifferprodukten
10. En kub
11. Delbart med 9
13. Det sista talet som stryks när man utför Eratosthenes såll på tal upp till 100
Lodrätt:
1. En kvadrat
2. Det minsta femsiffriga talet med alla siffror olika
3. Fibonaccital
4. Ett tal med exakt 12 delare
5. En tvåpotens
8. Ett kvadrattal med siffrorna i stigande ordning
9. Summan av fyra på varandra följande primtal
10. Minsta talet med exakt 8 delare
12. En kub
Ett väldigt delbart tal
Ett väldigt delbart tal
[kkratings]
Talet 310 är delbart med både 31 och 10. Hitta på ett så stort tal som möjligt, som är delbart med alla tvåsiffriga tal som grannsiffrorna i talet utgör. Det är inte tillåtet att ha nollor inuti talet eller upprepade tvåsiffriga segment.
Ovanlig sudoku
Försök att lösa! Som vanligt ska varje stor ruta, varje rad och varje kolumn innehålla alla 9 siffrorna en gång var.
Problem vecka 8. Tävlingsstart!
Kuben (1 poäng). En träkub har sidlängden 1 m. Vi sågar upp kuben i små kuber som alla har sidlängden 1 cm och lägger alla småkuberna på en rad. Hur lång blir raden?
Siffertriangeln (3 poäng). Går det att fylla de gula cirklarna med siffrorna från 0 till 9, så att summan längs med valfri av de 6 sträckorna blir densamma?
Visa lösningar
Lösning till problem vecka 21
På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir fyrsiffrigt?
Lösning:
Jadå, det kan han, till och med på flera olika sätt. Det här är Jonnes sätt, varje pil betyder att Daniel byter plats på siffror i talet:
123 -> 132
234 -> 243
345 -> 354
456 -> 465
567 -> 576
678 -> 687
789 -> 798
900 -> 009
111
213 -> 123
Följden är periodisk, det vill säga vi kan varje gång komma tillbaka till startsituationen. Därför kommer talet aldrig bli fyrsiffrigt.
Matteproblem vecka 21
På dataskärmen står ett tal, som varje minut ökar med 102. Från början står det 123. Programmeraren Daniel kan när som helst ändra ordningen på siffrorna i talet på dataskärmen. Kan han garantera att talet aldrig blir fyrsiffrigt?
Lösning till problem vecka 16
Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112… Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av exakt lika många siffror. Kan den första dagen vara oövermålad eller måste den vara övermålad?
För andra gången på kort tid använder jag mig av Erik R.’s lösning :)
Lösning:
Antag att den första dagen är omålad.
Det finns ett ojämnt antal ensiffriga dagar. Det innebär att om den första övermålade dagen är en tvåsiffrig dag, så måste det omålade området vänster om den ha ett ojämnt antal siffror.
Men det går inte, därför då måste även de andra omålade områdena, som består av tvåsiffriga tal, ha ett ojämnt antal siffror. Således måste den första övermålade dagen vara ensiffrig.
Men om den första övermålade dagen är ensiffrig, så har det omålade området vänster om den maximalt 8 siffror. Eftersom tre målade dagar som mest kan dela in sifferraden i fyra omålade områden kan det totala antalet siffror då max vara 8*4+1+2+2=37.
Men den kortaste månaden (februari i ett vanligt år) ger 9*1+19*2=47 siffror. Därmed kan ingen månad täckas in på detta vis.
Den första dagen måste därmed vara övermålad.
Matteproblem vecka 16
Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112… Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av exakt lika många siffror. Kan den första dagen vara oövermålad eller måste den vara övermålad?
Okänd sifferkod
Rekommenderad från: 12 år
[kkratings]
En sifferkod, som består av 7 olika siffror kallas för godkänd sifferkod. Man vet att ett kassaskåp har en viss okänd godkänd sifferkod.
Om man slår in någon godkänd kod och åtminstone en rätt siffra kommer på rätt plats, så öppnas kassaskåpet.
Kan man öppna kassaskåpet på färre än 7 försök?
