Fibonaccitalen och gyllene snittet

Ett välkänt trick är att man kan klippa en triangel i bitar, arrangera om bitarna, sätta ihop dem till en triangel igen och få en extra ruta!

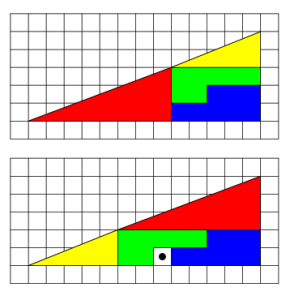
Hur kan det stämma? Nedan kommer förklaringen, men fundera själv först!

.

.

.

.

.

.

.

.

De stora figurerna är egentligen inte trianglar, det ser bara ut som det. Vore de riktiga trianglar, skulle den gula och den röda triangeln vara likformiga, det vill säga ha samma förhållande på kateterna. Men $\frac{5}{2}\neq\frac{8}{3}$ (eftersom $\frac{3}{2}\neq\frac{8}{5}$ ).
Så att den första figuren är en inåtböjd ”triangel” och den andra är en utåtböjd. Därifrån kommer den extra rutan.

Låt oss jämföra liknande, men annorlunda bråk: $\frac{3}{2}$ och $\frac{8}{5}$ .
$\frac{3}{2}=1,5$

$\frac{8}{5}=1,6$
Ganska nära värden! Därför har även $\frac{5}{2}$ och $\frac{8}{3}$ ganska nära värden. Förhållanden mellan sidorna är så pass lika att trianglarna är nästan likformiga och har nästan likadana vinklar. Det innebär att deras hypotenusor bildar nästan en linje (och för oss ser det ut som att de bildar en linje).

Låt oss studera fler förhållanden:

$\frac{13}{8}=1,625$

$\frac{21}{13}=1,61538462\ldots$

$\frac{34}{21}=1,61904762\ldots$

$\frac{55}{34}=1,61764706\ldots$

$\frac{89}{55}=1,61818182\ldots$

Den noggranna läsaren kanske har upptäckt att de nya täljarna får man genom att addera de föregående två:

$21=13+8$

$34=21+13$

$55=34+21$

$89=55+34$

Och några känner igen Fibonaccitalen i nämnarna och täljarna:

$1,1,2,3,5,8,13,21,34,55,89\ldots$

Fibonaccitalen startar med 1 och 1, sedan får man nästa tal genom att lägga ihop de två föregående.

Låt oss se om bråken (som är lika med förhållanden mellan två Fibonacci-granntal)

$\frac{2}{1},\frac{3}{2},\frac{5}{3},\frac{8}{5},\frac{13}{8},\frac{21}{13},\frac{34}{21},\frac{55}{34},\frac{89}{55},\ldots$

i slutändan blir lika med något värde. Vi har ju sett på de tidigare att värdet verkar vara nära $1,6$ .

Man kan skriva om bråken till så kallade kedjebråk:

$\frac{2}{1}=1+\frac{1}{1}$

$\frac{3}{2}=1+\frac{2}{1}=1+\frac{1}{\frac{2}{1}}=1+\frac{1}{1+\frac{1}{1}}$

$\frac{5}{3}=1+\frac{2}{3}=1+\frac{1}{\frac{3}{2}}=1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}$

Varje bråk blir lika med 1+1/(föregående bråk) och därför ser alla de bråken ut på ett och samma sätt. Det är bara antalet ettor i kedjebråket som ökar för varje steg.

Låt oss anta att vi får något reellt tal $\varphi$ , om vi utför operationen oändligt många gånger:

$\varphi=1+\frac{1}{1+\frac{1}{1+\ldots}}$

Då måste

$1+\frac{1}{\varphi}=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ldots}}}=\varphi$

$\varphi=1+\frac{1}{\varphi} \iff \varphi^2-\varphi-1=0$

Ekvationen har exakt en positiv lösning:

$\varphi=\frac{1+\sqrt{5}}{2}\approx 1,61803399$

Detta tal kallas gyllene snittet och är lika med vissa proportioner i Da Vincis målning ”Den vitruvianske mannen”. Många andra saker i naturen har den proportionen också, just på grund av att mycket i naturen beter sig som Fibonaccital (se början på videon):

Om du tyckte om Fibonaccitalen försök att lösa följande två problem:

1. Klipp upp en kvadrat med sida 1 i tre eller fyra delar och sätt ihop delarna till en rektangel med sidorna $\varphi$ och $\varphi-1$ .

2. Klipp upp en kvadrat med sida 8 i tre eller fyra delar och sätt ihop delarna till en nästan rektangel med sidorna 5 och 13. (Du kan öka Fibonaccitalen i problemet och se ”felet försvinna”.)

(Bonusproblem. Bråken
$\frac{5}{2},\frac{8}{3},\frac{13}{5},\frac{21}{8},\frac{34}{13},\ldots$
närmar sig ett värde. Vilket?)

Jag tackar Djalal för tipset om ovanstående problem och diskussion.

Relaterade

8 reaktioner till “Fibonaccitalen och gyllene snittet”

Henrik Valentin skriver:

09 augusti 2011 kl. 14:37

Snygg och intressant blogg. Det går att göra matte roligt. I min roman Ödelagd jobbar huvudpersonen, en svensk- och engelsklärare tillsammans med bl a en mattelärare. De drar igång ”Mattesvenska” för att förbättre läsförståelse och mattekunskaperna. http://www.odelagd.se/2011/07/underkant-for-matte-2/
Val skriver:

12 augusti 2011 kl. 8:34

Tackar! Vore spännande att se hur nätresurser verkligen tillämpas i matteundervisningen i Sverige.
Filiz skriver:

19 augusti 2011 kl. 18:43

Verkligen ett udda trick, det är så svårt att se skillnaden mellan de två figurerna men om man sätter sig ner och räknar på areorna går dem ju inte ihop. Men ändå, en kul grej…XD
Val skriver:

20 augusti 2011 kl. 9:44

Jag, det är svårt att se med blotta ögat. Jag har försökt markera den arean som tillkommer med svart. Det ser ut som ett streck, men det är egentligen en parallellogram.
Anonym skriver:

12 januari 2014 kl. 22:24

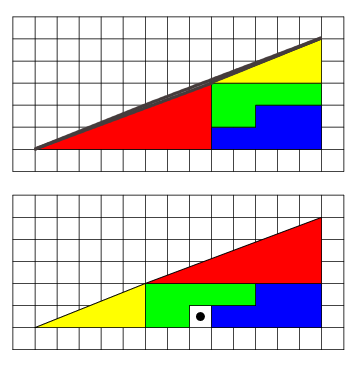
har de olika figurerna samma area?
Val skriver:

12 januari 2014 kl. 22:28

Figurer med samma färg är exakt likadana och har samma area.
Anonym skriver:

13 januari 2014 kl. 15:57

det jag undrar är om den övre triangeln och den undre triangeln har samma area
Val skriver:

13 januari 2014 kl. 17:49

Trianglarna har samma area. Basen för båda är 13 och höjden är 5. Men är du säker på att de är trianglar? ;)