algoritm – Mattebloggen

Två bokhögar

Rekommenderad från: 12 år

[kkratings]

På ett bord ligger en boksamling av barnböcker i 10 delar, uppdelade i två högar. Du får ta tag i en stapel (några av de översta böckerna i en hög, som minst en, som mest hela högen) och placera den överst på den andra högen.

Hur kan man på 19 sådana operationer eller färre se till att alla böckerna ligger i en hög och delarna är ordnare (det vill säga, del 1 ligger underst, del 2 ligger näst underst och så vidare)?

bokhog

Visa lösningen

Böcker kan ligga hur som helst i början, men vi vet att de ligger i två högar på något sätt, och del 1 måste vara i en utav högarna. Låt oss först se till att just del 1 hamnar underst i en hög.

Ta då tag i högen som inte innehåller del 1 och lägg det överst på den andra högen. Allt ligger nu i en hög. Ta sedan tag i stapeln som har del 1 som understa bok och lyft över allting till den tomma platsen. Nu har vi en hög med del 1 underst och en annan hög, vilket ha tagit oss 2 operationer. Högst 2 egentligen, om del 1 redan låg på rätt plats från början.

Oavsett var del 2 ligger nu gör vi följande process. Lyfta bort alla eventuella böcker som ligger på del 1 och placera den stapeln på andra högen. Eftersom del 2 nu finns i den högen, lyft stapeln som har den delen underst och placera alltihop på del 1. Detta tog oss (högst) 2 operationer.

Gör samma sak med del 3: lämna först del 1 & del 2 ensamma och sedan lyft över stapeln med del 3 underst dit. Igen (högst) 2 operationer.

Fortsätter man på samma sätt kommer del 4, del 5, del 6, del 7, del 8 ta högst 2 operationer var. Vi har nu förbrukat 16 operationer, så det är 3 kvar.

Hur kan högarna se ut nu? I en hög ligger del 1 till del 8 i rätt ordning och på dem ligger eventuellt några böcker.

Om del 9 och del 10 råkar ligga ovanpå dem i rätt ordning, så är vi klara. Om de råkar ligga i fel ordning, lyft bort de båda och sedan lägg dem tillbaka en i taget (del 9 kommer vara först med att läggas på den stora stapeln, sist kommer del 10), det kommer ta (högst) 3 operationer.

Om både del 9 och del 10 ligger i den andra högen, lägg dem över antingen båda på en gång (om del 9 är underst), eller en i taget (om del 10 är underst), detta kommer ta (högst) 3 operationer.

Om den lilla högen bara innehåller del 10, så tar det 1 operation att lägga över den och få sorterad stapel. Om den lilla högen bara innehåller del 9, är det lite svårare. Då lägger vi över del 10 till den lilla högen, och sedan lägger tillbaka del 9 & del 10 tillsammans, och får en sorterad stapel. Detta tog alltså (högst) 2 operationer.

Oavsett hur det ser ut på slutet, tar det alltså högst 3 operationer. Vi klarade således att sortera bokhögen på högst 19 operationer!

Aladdin och grottan

Rekommenderad från: 12 år

[kkratings]

Aladdin vill komma in i grottan, men dörren än stängd. Innanför grottan finns en tunna med fyra hål (hålen är likadana och är placerade som hörnen på en kvadrat). I varje hål finns en karaff med en fisk inuti. Varje fisk kan antingen ligga med huvudet eller stjärten upp. Aladdin kan stoppa in händerna i två av hålen, känna efter hur fiskarna ligger där och vända på ingen fisk eller en fisk eller båda om han vill. Efter det snurrar tunnan och när den stannat kan han inte avgöra vilka hål han stoppade händerna i förra gången. Dörren till grottan öppnas när alla 4 fiskar ligger likadant. Aladdin har 5 försök på sig. Kommer han att kunna komma in?

Visa lösningen

Kamelen och bananerna

En kamel odlar bananer. Det här året fick han bästa skörden någonsin: 3000 bananer! Men tyvärr ligger den närmaste platsen där han kan sälja bananerna 1000 km bort. Kamelen kan bara bära 1000 bananer i taget och på vägen måste han äta 1 banan per kilometer.

Vad är det största antalet bananer kamelen kan sälja?

Visa lösningen

Komma över till andra sidan

Kanske har du hört problemet om bonden och hans ägodelar. Det här är en annan variant på problemet!

Komma över till andra sidan

Det finns en båt med plats för tre och en av platserna är reserverad åt bonden. Bonden måste komma över till andra sidan floden tillsammans med en get, ett kålhuvud, två vargar och en hund. Men hunden bråkar alltid med en varg, geten vill äta upp kålhuvudet och varken en varg eller hunden kan vara ensamma med geten (detta sker om bonden inte håller ett vakande öga på dem).

Hur ska de alla ta sig över till andra sidan utan problem?

Visa lösningen

Problem om att ta sig över till andra sidan

Året var 1997. Det var då jag började ha matematiska framgångar och blev därmed skickad på en resa till den stora staden Moskva. Där skulle jag och andra 6:or och 7:or tävla i problemlösning. Som jag minns det gick det hyfsat ok för mig, men ett problem kunde inte de flesta deltagarna lösa:

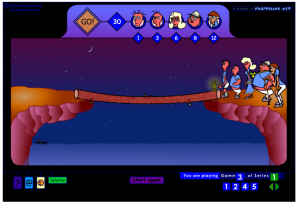
En familj kommer fram till en bro mitt i natten. Pappan kan gå över bron på 1 minut, mamman – på 2 minuter, barnet – på 5 minuter och mormorn – på 10 minuter. De har bara en lykta. Bron håller bara för två personer åt gången. Hur ska alla ta sig över till andra sidan på 17 minuter? (Om två personer går över samtidigt, går båda lika snabbt som den långsammaste av dem. Man får inte gå på bron utan lyktan. Man får inte lysa långt bortifrån. De får inte bära varandra.)

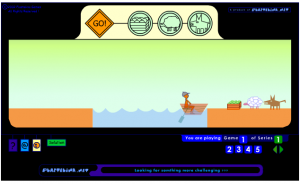
Ännu tidigare i min matematiska karriär hörde jag talas om problemet om Bonden och hans ägodelar:

En man ska ta sig över en å i en roddbåt. Han medför en varg, en get och ett kålhuvud. Han kan inte ta med sig mer än en av ägodelarna åt gången. Vargen kan inte lämnas ensam med geten och geten kan inte lämnas ensam med kålhuvudet. Hur skall mannen bära sig åt för att klara övergången?

Kanske vet du lösningen, kanske inte. Det är roliga är att numera finns problemet i form av ett spel!

Prova även att få över missionärer och kannibalen till andra sidan. Båten rymmer två, men blir det fler kannibaler än missionärer på någon sida, blir missionärerna uppätna.

Och till slut kan du prova att få över familjen med lyktan på andra sidan. Den här familjen är dock lite större än i problemet i början, och har lite annorlunda tider. Men illustrationen till problemet är suverän.

Alla ni som tyckte om problemen om familjerna, kan försöka lösa det generella fallet. Vilket är den minsta tiden att ta alla över till andra sidan, om familjen har $n$ medlemmar som tar sig över på $a_1, a_2, \ldots, a_n$ minuter där $a_1\leq a_2\leq\ldots\leq a_n$ ?

Lösningen till problemet för de äldre vecka 47

Mattegåta

I tio likadana kannor finns lite mjölk: varje kanna är full till max 10%. En tillåten operation är att ta en valfri kanna och hälla av en del av mjölken till de andra kannorna (lika mycket till varje övrig kanna).

Visa att 10 operationer räcker för att få kannorna att innehålla exakt lika mycket mjölk.

Diskussion

För det första kan kannorna innehålla väldigt ojämna mängder av mjölk, så det, att kannorna är fulla till max 10%, säger är att vi alltid kan hälla över mjölk, det blir alltså aldrig för fullt i någon kanna.

Vi ska få till lika mycket mjölk i varje kanna. Det känns inte som om vi kan hoppas på den sista överhällningen. Om det är ojämnt i många kannor, kan inte en enda överhällning (som ju häller lika mycket i varje icke-vald kanna) få alla kannorna att innehålla lika mycket. Alltså måste vi börja fixa kannor med lika mycket mjölk redan i början.

Börjar man på ett smart sätt får man att 9 operationer räcker.

Lösning (av Erik Svensson)

För att fördela mjölken jämnt mellan kannorna, låt oss använda följande algoritm:

Om alla kannorna har lika mycket mjölk i sig, då är vi klara. Annars kommer någon kanna ha mest mjölk och någon annan ha minst mjölk (om flera har mest eller minst väljer vi godtyckligt bland dessa), och mellan dem finns en viss skillnad i hur mycket mjölk de innehåller. Från den med mest mjölk häller vi till varje annan kanna en tiondel av denna skillnad. På det viset kommer den mest mest mjölk förlora nio tiondelar av skillnaden, och den med minst mjölk ökar med en tiondel av skillnaden, och således kommer de efteråt att innehålla lika mycket mjölk. Alla kannor, utom den vi häller ifrån, ökar sitt mjölkinnehåll lika mycket, vilket innebär att den kanna som hade minst mjölk innan operationen fortfarande kommer ha minst mjölk, tillsammans med den som nyss hade mest mjölk.

Sedan upprepar vi detta. För varje iterering tar vi den kanna som har mest mjölk och ser till att den jämnställs med alla kannor som har minst mjölk. Dessa kannor ändras inte i förhållande till varandra, och alltså kommer vår algoritm på detta vis att öka antalet såna jämnställda kannor med ett vid varje iterering. Efter högst tio itereringar kommer således alla kannor innehålla minst mjölk, det vill säga, de innehåller alla lika mycket mjölk.