fyrhörning – Mattebloggen

Fyrhörningens diagonal

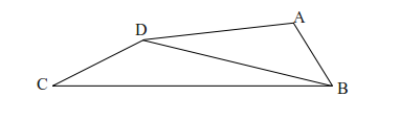
I fyrhörningen ABCD är AB = 5 cm, BC = 17 cm, CD = 5 cm, DA = 9 cm och sträckan BD är ett helt antal cm. Hur lång är sträckan BD?

Bilden är inte exakt, utan endast schematisk

Visa lösningen

Feta streck

[kkratings]

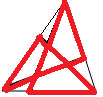
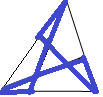
Triangeln på bilden är uppdelad i fyra trianglar och tre fyrhörningar med de feta strecken.
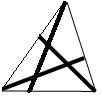
feta_streck

Fyrhörningarnas omkretser tillsammans är 25 cm. Summan av omkretsarna för de fyra trianglarna är 20 cm. Den stora ursprungliga triangelns omkrets är 19 cm. Bestäm summan av längderna av de feta strecken.

Visa lösningen

Klurig fyrhörning

Rekommenderad från: 17 år

[kkratings]

En konvex fyrhörning ABCD har kända sidlängder: AB = 5, BC = 10, CD = 14, DA = 11. Fyrhörningens diagonaler skär varandra med en viss vinkel. Hur stor är den vinkeln?

Visa lösningen

En lektion för små barn om kvadrater (och andra fyrhörningar)

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.

Här kan du se vad vi tidigare har gått igenom.

Fyrhörningar

Vad är en fyrhörning? Hur många sidor har den och hur många hörn? Kan alla rita en fyrhörning?

Vad är en rektangel? Varför heter den så (på ryska heter det något i stil med ”rätvinkling”)? Om du ska bygga en rektangel av pinnar, vad väljer du då för längder på pinnarna?

Vad är en kvadrat? Är en kvadrat en rektangel? Är en kvadrat en fyrhörning?

Vad kallas en fyrhörning där alla sidor är lika långa? Är en romb alltid en kvadrat? Är en kvadrat alltid en romb?

Rita en romb

Alla får ett rutat papper. Börja med att sätta ut en punkt någonstans (helst i korsningen mellan två linjer). Sedan sätt ut två punkter, en till höger och en till vänster, på samma avstånd från startpunkten. Det vill säga, räkna samma antal rutor till vänster respektive till höger och sätt ut nya punkter. Gör samma sak uppåt och neråt från startpunkten, men nu kan det vara ett annat avstånd. Rita sidorna i den fyrhörningen som alla nya punkterna bildar. Du får en romb!

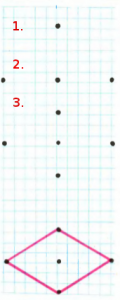
Fråga: kan man rita en kvadrat på det här sättet?

Bevisa vilken form det är

Barnen får titta på olika figurer: godtyckliga fyrhörningar som är konvexa eller konkava, rektanglar, romber, kvadrater. De måste säga alla namn som figuren kan kallas och bevisa det också, men hjälp av linjal och ett bord (med linjalen kan de mäta ifall sidorna är lika långa och medelelst bordet kan de visa att en speciell vinkel är rät).

Till exempel denna figur än en fyrhörning och en romb:

Varför fyrhörning?
– Den har fyra sidor och fyra vinklar.

Varför romb?
– Alla sidorna är lika långa (verifieras mha linjal, eller så viker man den och sätter sidorna mot varandra)

Denna figur än en fyrhörning:

Varför fyrhörning?
– Fyra sidor, fyra hörn

Varför inte rektangel?
– Två av vinklarna är räta, men inte alla fyra (rät vinkel ”bevisas” genom att sätta figuren mot bordshörnet). Eller, en annan motivering: de två motstående sidorna är inte lika långa.

Ett närmare titt på kvadrater

Alla aktiviteterna nedan handlar om kvadrater, men de är egentligen väldigt olika. En del går ut på kombinatoriskt tänkande, en del på geometriskt. Det är viktigt att tänka antal, storlek, symmetri, mönster. Och det viktigaste av allt är att vara kreativ!

Kvadratuppdelning

Hur kan man dela upp en kvadrat i fyra likadana figurer? Nedan ser ni några exempel, men egentligen finns det oändligt många sätt.

Tändsticksproblem

Tändstickorna är en klassiker!

På bilden nedan finns fem kvadrater.
Hur ska man kunna ta bort två tänkstickor, så att det blir tre kvadrater kvar? Och två kvadrater?

Kvadrattal

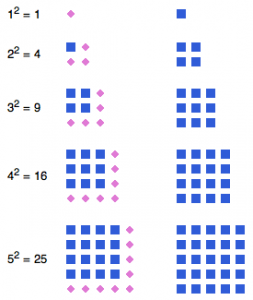
Med de äldre barnen kan vi undersöka kvadrattal. Av små kvadratiska leksakstorn får de bygga de olika stora kvadraterna en i taget. Hur mycket bygger man på i varje steg (svar: de udda talen 1,3,5,7 och så vidare).

Vika transitivt

De flesta vuxna kan få en kvadrat utav ett rektangulärt papper: man viker ihop ena hörnet så att det bildas en rätvinklig triangel (som är två lager av papper). Sedan är det bara att klippa bort/vika in den överflödiga lilla rektangeln.

Men hur gör man för att få en kvadrat av en rätvinklig triangel med inga hjälpmedel?

Och hur får man en kvadrat ut en godtycklig triangel?

Det här problemet löses i flera steg och bygga på transitivetetsprincipen. Om vi kan göra om en rektangel till en kvadrat och sedan lär oss att göra om en rätvinklig triangel till en rektangel, kan vi alltså alltid göra om en rätvinklig triangel till en kvadrat.

Godtycklig triangel -> rätvinklig triangel
Hitta en höjd inuti triangeln. Vik längs med den (det vill säga, vik ihop hörnet så att den motsatta sidans delar läggs på varandra). Voila! En rätvinklig triangel.

Rätvinklig triangel -> rektangel
Vik båda kateterna på mitten, det vill säga vik in de spetsiga hörnen. Vi har en rektangel (pga topptriangelsatsen).

Rektangel -> kvadrat
Om ena av rektangeln sidor inte är dubbel så lång eller längre som den andra, gör som ovan. Annars, vik som ovan flera gånger, tills ”restrektangeln” är tillräckligt liten. Eller klipp bort efter första steget, om sax är tillåtet.

Vika boxar

Nu när vi kan göra kvadrater av lite vad som helst, kan vi lära oss att vika ihop boxar. Fördelen med de här boxarna är att man inte behöver vara supernoggrann, för att det ska bli ett hyfsat resultat. Problemet med de små barnen och origami är att de oftast inte har precision nog att vika en vinkel exakt på hälften. Äsch, inte ens alla vuxna har den precisionen!

Problem vecka 18

Cirkelkonstruktion (2 poäng).
Du har en passare, som du kan rita cirklar med (så länge du känner till cirkelns mittpunkt och dess radie) samt en ograderad linjal, som du inte kan mäta något med, men som du kan rita en linje med genom två valfria punkter.

Du har fått ett papper där en cirkel c är ritad (och dess mittpunkt är markerad) och där en punkt A utanför cirkeln är markerad.

Hur kan du med hjälp av dina verktyg rita en ny cirkel, som har A som mittpunkt och som precis tangerar den redan ritade cirkeln c? Bevisa att din konstruktion ger korrekt resultat.

Cosinussumman (5 poäng).
Visa att ifall summan av cosinusar på vinklarna hos en fyrhörning är lika med 0, så måste fyrhörningen antingen vara cyklisk, en parallellogram eller ett parallelltrapets.

Visa lösningar

Cirkelkonstruktion (Davids lösning):
Låt B vara mittpunkten i cirkeln c. Drag sträckan AB. Låt X vara punkten där AB skär c. Rita en cirkel med mittpunkt i A och som går genom X. Jag vill visa att denna cirkel tangerar c. De har ju en gemensam punkt X, så jag vill visa att de inte har någon annan gemensam punkt.

Antag att de har en annan gemensam punkt Y. Då finns det två sätt att gå från A till B: via X (vägens längd är |AX|+|XB|) eller via Y (vägens längd är |AY|+|YB|). AX och AY är radier i vår konstruerade cirkel, alltså |AX|=|AY|. XB och YB är radier i c, alltså |XB|=|YB|. Alltså |AX|+|XB|=|AY|+|YB|. Men när vi går via X följer vi en rät linje enligt vår konstruktion, så ingen annan väg från A till B kan vara lika kort. Vilket motsäger att vägen via Y är lika kort. En motsägelse som visar att vår cirkel och c har en och endast en gemensam punkt, alltså tangerar de varandra.

Cosinussumman (Skäggets lösning):
Vi börjar med att konstatera att ett parallellogram är ett specialfall av en parallelltrapets, så vi visar bara att en fyrhörning är antingen cyklisk eller en parallelltraptes om summan av cosinus av vinklarna är 0.

Låt oss kalla vinklarna i vår fyrhörning för A, B, C och D (med ordningen än så länge godtycklig).

Vi vet att summan av vinklarna i en fyrhörning är 360 grader, och vi kommer använda följande identitet för cosinus:

$cos X + cos Y = 2\ cos(\frac{X+Y}{2})\cdot cos(\frac{X-Y}{2})$

Vi antar nu att summan av cosinus av alla vinklar är noll, det vill säga:

$cos A + cos B + cos C + cos D = 0$

$\iff 2\ cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})+2\ cos(\frac{C+D}{2})\cdot cos(\frac{C-D}{2})=0$

$\iff cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=-cos(\frac{C+D}{2})\cdot cos(\frac{C-D}{2})=0$

Vi vet att D = 360 – A – B – C, samt att cos (180 – X) = – cos X. Detta ger oss:

$cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=-cos(\frac{360-A-B}{2})\cdot cos(\frac{C-D}{2})$

$\iff cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=cos(\frac{A+B}{2})\cdot cos(\frac{C-D}{2})$

Lås oss anta att cos (A + B)/2 är skiljt från 0. Då får vi:

$cos(\frac{A-B}{2})=cos(\frac{C-D}{2})$

$\Rightarrow cos(A-B)=cos(C-D)$

$\Rightarrow A-B=\pm(C-D)$

Eftersom C och D är godtyckliga kan vi ignorera vårt +/- i högerledet, och vi får:

$A-B=C-D \iff A+D=B+C$

Vi får alltså att ifall cos (A + B)/2 är nollskiljt så kommer A,D och B,C vara par av supplementära vinklar.

Vi noterar att cos (A + B)/2 = 0 implicerar att (A + B)/2 = 90 eller 180, och alltså att A + B = 180 (ty A + B + C + D = 360, och alla vinklar är positiva, så A + B = 360 är ingen möjlighet).

Med andra ord, tar vi två godtyckliga vinklar i vår fyrhörning och kallar dem A och B, då gäller att A + B = 180 eller så är A + D = 180, där D är någon annan vinkel. Alltså är vi garanterade att vinklarna i vår fyrhörning är parvis supplementära.

Vi får två möjligheter, att intilliggande vinklarna är supplementära eller att motstående vinklar är det. Ifall de är intilliggande får vi att två sidor i vår figur är parallella, och vi har alltså en paralleltrapets. Och ifall motstående vinklar i en fyrhörning är supplementära, då är fyrhörningen cyklisk.

Sammanfattningsvis har vi alltså funnit att om summan av cosinus av alla vinklar är 0, då gäller att antingen så är varje vinkel supplementär till en intilliggande vinkel (och då är fyrhörningen en parallelltraptes) eller så är motstående vinklar supplementära (och där är fyrhörningen cyklisk), vilket skulle bevisas.

En följd av fyrhörningar

Rekommenderad från: 15 år

[kkratings]

Låt F₁ vara en godtycklig konvex fyrhörning. För k>1, F_k konstrueras genom att man skär F_k-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs samma diagonal. Bestäm det största möjliga antalet icke-kongruenta fyrhörningar i följden {F_k}.

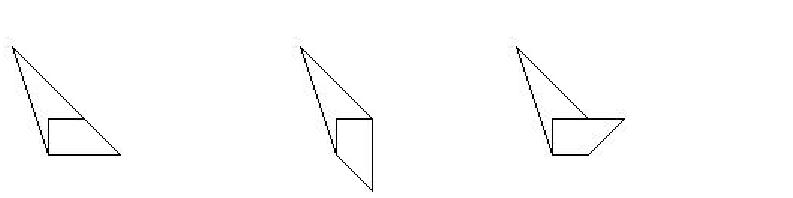
Exempel:

För att förtydliga, en tillåten operation är följande:

lv25_1

Visa lösningen

Notera att om sidlängderna hos fyrhörningen är a, b, c, d, så finns exempel, där följden av fyrhörningar innehåller 6 icke-kongruenta: de med olika ordning på sidorna. Tag nämligenen fyrhörning med alla sidor olika, men som ändå påminner om en kvadrat (detta för att fyrhörningarna som bildas inte ska bli icke-konvexa). Men tillåtna operationer byt sedan plats på sidorna på alla möjliga sätt (trianglar med den gråa symbolen flippas):

l25

Ritningen är inte exakt, men vi kan se att alla olika sidordningar verkligen förekommer. Eftersom fyrhörningar kan roteras, valde vi fixera sidan med längden a, den kommer ändå alltid finnas.

Så nu är frågan varför det inte går att konstruera fler fyrhörningar? Notera att det finns en sak som aldrig förändras och det är summan av två motsatta vinklar i fyrhörningen. Vid varje flipp är det ett par av motsatta vinklar som inte ändras, således kommer vinkelsumman i det andra paret inte heller förändras.

Men notera också att sidlängderna kvarstår. Tag nu någon ordning på sidorna, vi skall nu bevisa att det går att bygga exakt en fyrhörning med den ordningen ur den ursprungliga. Utan inskränkning kan vi anta att sidordning är (medurs) a, b, c, d och a är den vänstra sidan.

Kalla vinkeln mellan a och d för x. Då är vinkeln mellan b och c också bestämd, nämligen S-x, där S var vinkelsumman av den ”nedre vänstra” och den ”övre högra” vinkeln. Men då har vi två trianglar, beståndsdelarna i fyrhörningen, som kan sättas ihop endast på ett sätt och det endast när de okända sidorna är lika (de ska bli en diagonal).

l25_2

De okända sidorna är lika endast för en vinkel x (den som det går att konstruera bilden för). Det beror på att om vinkeln minskas, så minskas också den motstående sidan. Men då ökar S-x och dess motstående sida, och då kan de sidorna inte längre vara lika. Samma sak händer om vinkeln x ökas.

På så sätt har vi uttömt alla fallen och visat att antalet olika fyrhörningar är 6, en för varje sidordning.

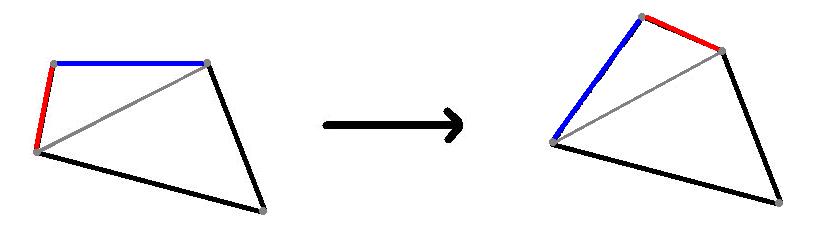
Två fyrkanter

Rekommenderad från: 12 år

[kkratings]

Rita två fyrkanter, som tillsammans kan läggas ihop till

(i) En triangel, men också en femkant

(ii) Både en triangel, en fyrkant och en femkant.

Med ”läggas ihop” menas att fyrkanterna inte får överlappa varandra, inte heller får det bildas hål.

Visa lösningen

Fyrhörningens diagonal

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Feta streck

Rekommenderad från: 17 år

Fyrhörningar

Rita en romb

Bevisa vilken form det är

Ett närmare titt på kvadrater

Kvadratuppdelning

Tändsticksproblem

Kvadrattal

Vika transitivt

Vika boxar

Visa lösningar

Rekommenderad från: 15 år

Exempel:

Rekommenderad från: 12 år