Kubkonstruktion
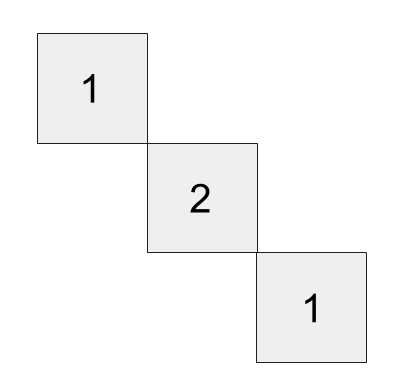
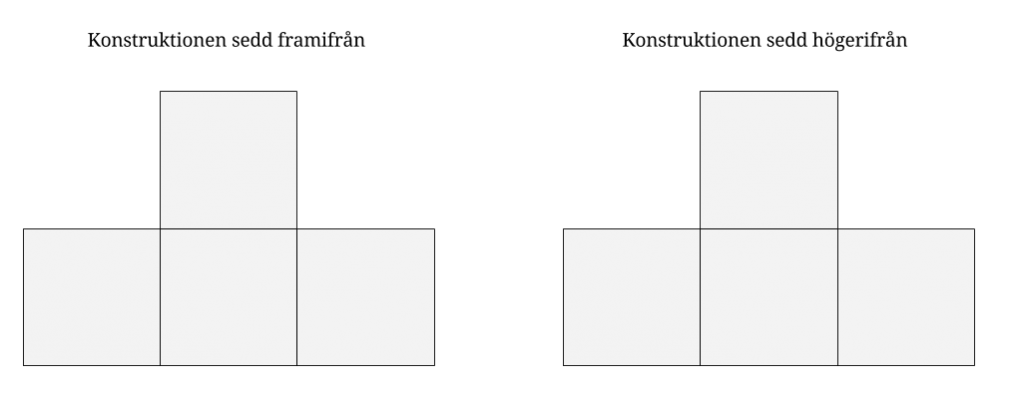
En konstruktion som är byggd av likadana kuber ser ut på samma sätt både framifrån och högerifrån. Vilket är det minsta antal kuber som konstruktionen kan bestå av? (Konstruktionen följer fysikens lagar.)
Tjocka och tunna hårband
Tjocka och tunna hårband
[kkratings]
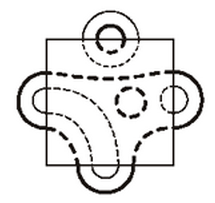
På bordet ligger sex hårband som inte nuddar varandra. Ovanpå dem ligger ett papper som delvis täcker dem (se bild). Man vet att tre av hårbanden är tunna, medan tre är tjocka och att banden kan vara olika långa. Fem av hårbanden syns lite, medan det sjätte är helt täckt.
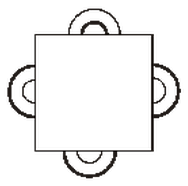
Vilken sorts hårband är helt täckt: ett tunt eller ett tjockt? Och hur kan det se ut under pappret?
Som svar räcker det att skicka in en bild där det tydligt framgår hur hårbanden ligger under pappret.
Världens mest matematiska flagga
Fråga: Vilket land har längsta matematiska texten i sin konstitution?
Svar: Nepal, som har inkluderat den geometriska konstruktionen av sin flagga i konstitutionen. Landet är dessutom den enda i världen vars flagga inte är rektangulär.
Spänd tråd
[kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.

Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla spikarna. Hur gör du?
Problem vecka 18
Cirkelkonstruktion (2 poäng).
Du har en passare, som du kan rita cirklar med (så länge du känner till cirkelns mittpunkt och dess radie) samt en ograderad linjal, som du inte kan mäta något med, men som du kan rita en linje med genom två valfria punkter.
Du har fått ett papper där en cirkel c är ritad (och dess mittpunkt är markerad) och där en punkt A utanför cirkeln är markerad.
Hur kan du med hjälp av dina verktyg rita en ny cirkel, som har A som mittpunkt och som precis tangerar den redan ritade cirkeln c? Bevisa att din konstruktion ger korrekt resultat.
Cosinussumman (5 poäng).
Visa att ifall summan av cosinusar på vinklarna hos en fyrhörning är lika med 0, så måste fyrhörningen antingen vara cyklisk, en parallellogram eller ett parallelltrapets.
Visa lösningar
Parkering
Rekommenderad från: 10 år
[kkratings]
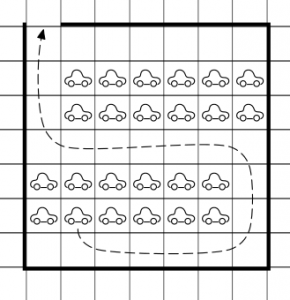
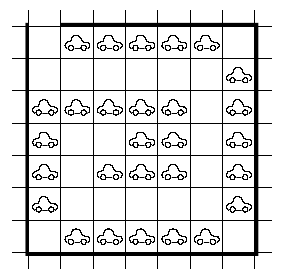
I staden Bilköping finns en parkering med plats för 7×7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som möjligt, men så att varje bil kan komma ut samtidigt som alla de andra står stilla. På bilden lyckades han göra så med 24 bilar.
Försök att placera ut så många bilar som möjligt!