dimension – Mattebloggen

Måla kubens yta

[kkratings]

För att måla ytan på en kub av storleken 2x2x2 krävs det 2 gram färg. Hur mycket färg krävs det för att måla ytan på en kub av storleken 6x6x6?

Visa lösningen

Det är lätt att med experiment uppskatta volymer av olika tredimensionella kroppar: Exempelvis kan ett akvarium i from av en rätblock fyllas med vatten och sedan kan man mäta hur mycket vatten som gick åt. Samma kan göras med (ungefär) sfäriska behållare. Med matematik kan man bevisa att formeln för volymen av en tredimensionell boll är $\frac{4}{3}\pi R^3$ , vilket redan Arkimedes visade på den gamla goda tiden.

vatten_boll

Svårare är det när objekt har 4 eller fler dimensioner. Vi har inte längre några fysiska experiment vi kan göra, men för matematiken spelar det mindre roll hur många dimensioner det handlar om. Bollar i olika dimensioner är nämligen väldigt lika varandra om man tittar på dem med hjälp av ekvationer. Men låt oss börja från början.

Vad är en 1-dimensionell boll? Det är ju alla punkter på en linje, som ligger på ett givet avstånd från en given punkt eller närmare. Med andra ord, ett intervall. Om det givna avståndet, det vill säga radien, är lika med $R$ , så är intervallets längd lika med $2R$ . Det kan vi kalla formeln för volymen av en 1-dimensionell boll (väldigt fancy sätt att säga ”längd”).

En 2-dimensionell boll, som du säkert redan gissat, är en cirkel. På högstadiet (hoppas jag) lär man sig att cirkelns area är $\pi R^2$ om cirkelns radie är lika med $R$ . Volymen av en 2-dimensionell boll är således fastställd.

cirkel_area

Men hur räknar vi ut (hyper)volymen av en 4-dimensionell boll och hur definieras en sådan ens? Om vi ska fortsätta på samma sätt så måste vi definiera en $n$ -dimensionell boll på följande vis:

En $n$ -dimensionell boll med radie $R$ är ett område i $\mathbb{R}^n$ som innehåller alla punkter med koordinater $(x_1, x_2, \ldots, x_n)$ som uppfyller $x_1^2+x_2^2+\ldots+x_n^2\leq R^2$ .

Men hur ska vi ta reda på bollens volym? Genom att uttrycka den via de föregående volymerna! Volymen av bollen med radien $R$ i $n$ dimensioner, $V_n(R)$ , hänger nämligen ihop med volymen av bollen i $n-2$ dimensioner, $V_{n-2}(R)$ , på följande sätt:

$V_n(R)=\frac{2\pi R^2}{n}V_{n-2}(R)$

Detta bevisas genom att man ”delar upp” $n$ -bollen i $(n-2)$ -bollar (exempelvis den vanliga tredimensionella bollen kan ses som en massa vertikala streck) och sedan beräknar en dubbelintegral.

Formeln räcker, eftersom vi känner till volymerna för $n=1$ och $n=2$ , alltså kan vi konstruera formlerna för alla högre $n$ också.

$V_3(R)=\frac{2\pi R^2}{3}V_1(R) = \frac{2\pi R^2}{3}2R = \frac{4\pi R^3}{3}$ , som vi har sett tidigare.

Hyperbollen då?

$V_4(R)=\frac{2\pi R^2}{4}V_2(R) = \frac{2\pi R^2}{4}\pi R^2 = \frac{{\pi}^2 R^4}{2}$

Fler dimensioner? Från rekursionen deducerar vi en formel för udda dimensioner och en för jämna:

$V_n(R) = \frac{2^{\frac{n-1}{2}}\pi^{\frac{n-1}{2}}R^n}{1\cdot 3\cdot\ldots\cdot n}$ om $n$ är udda och

$V_n(R) = \frac{2^{\frac{n}{2}}\pi^{\frac{n}{2}}R^n}{2\cdot 4\cdot\ldots\cdot n}$ om $n$ är jämnt.

Vad beräknas volymen till då om radien antas vara 1? Vi får följande tabell:

$n$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Volym, ca	2	3,14	4,19	4,93	5,26	5,17	4,72	4,06	3,30	2,55	1,88	1,34	0,91	0,60	0,38

Volymen går upp först men sedan verkar den gå det mot noll! Det intressanta är att trots att den 5-dimensionella bollen har störst volym av alla här, så är den egentligen inte så speciell. Om vi ändrar radien blir det någon annan dimension som ger en boll med störst volym (testa själv med hjälp av formeln, vid radie 1,29 är det istället den 9-dimensionella bollen som har störst volym.)

Det verkar lite skumt att volymerna går mot 0, men om man ser på formeln, så innehåller den exponentiella funktioner i täljaren, men i princip fakulteter i nämnaren. För stora tal dominerar fakulteterna alltid, alltså går kvoten mot 0 (och växer i början, för små $n$ , då fakulteterna inte än börjat ”ta fart”).

Ett annat sätt att tänka på det är att för att ekvationen $x_1^2+x_2^2+\ldots+x_n^2 = R^2$ ska vara uppfylld för stora $n$ måste många av talen $x_i$ vara nära 0. Exempelvis ligger punkten $(\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}}\ldots,\frac{1}{\sqrt{n}})$ på bollens yta och alla de koordinaterna närmar sig 0 när $n$ växer.

Texten ovan är baserad på följande artikel på engelska, som även innehåller beviset för rekursionsformeln. Stort tack!

Klassiska bevis: Monges sats

Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!

Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller tonårsben). Ju längre tid som går, desto mer måste man lära sig för att bli imponerad av något nytt tankesätt. Men som pris får man oftast upptäcka något ännu mer fascinerande än förra gången.

Ett av de här tillfälen var jag med om när jag för första gången besökte Uppsala. Det var någon gång vid årsskiftet 2001/2002 och jag gick i ettan på gymnasiet och kunde förstås inte så mycket om universitetsmatematik. Vilket i och för sig inte behövs för historien. Men snart får ni se hur allt ändå hänger ihop.

Vi fick sitta i ett klassrum och en matematiker berättade följade problem för oss.

Tre olika cirklar ligger i planet och de skär inte varandra (och ligger inte inuti varandra heller). För varje par av cirklar dra två linjer, som tangerar båda två cirklarna. Om cirklarna är olika stora, kommer dessa två linjer att skära varandra. Frågan är nu: kommer de tre erhållna skärningspunkterna att ligga på samma linje?

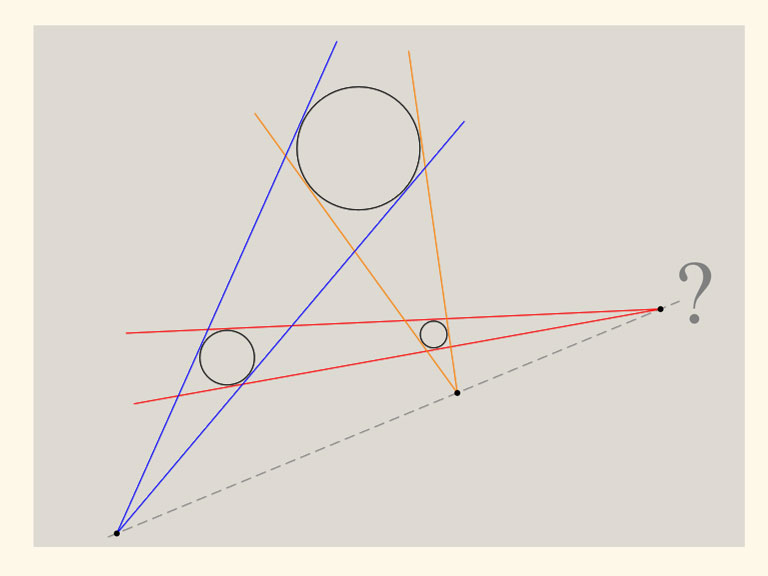
monge

Det visar sig att de måste. Försök att lösa problemet med den geometrin du kan. Det verkar vara svårt att visa, genom att bara rita linjer och bestämma vinklar i planet.

Däremot finns en elegant lösning, som använder sig utav en tredje dimension!

Varför och hur?

Det är en väldigt imponerande idé, att gå högre upp än vad som verkar behövas. Om problemet inte kan lösas, så skall man försöka att titta på det ur en annan synvinkel. Men oftast ligger svårigheten i att välja rätt synvinkel.

Just att gå upp i högre dimensioner visade sig vara nyttigt även i andra vetenskaper. Mycket förklarades av insikten om att jorden är sfärisk, extra dimensioner behövs för att strängteorin skall hålla. Även min forskning handlar om att förstå enklare strukturer genom att titta på de mer kompilcerade. Men hur hjälper den tredje dimensionen i vårt problem?

Föreställ er att det inte är cirklar, utan klot som ligger på ett plant papper, då ser det hela precis ut som på bilden om vi kollar uppifrån. Linjerna är fortfarande linjer, men i rymden kan vi faktiskt konstruera oändligt många linjer som är gemensamma tangenter till två av kloten. Alla dessa gemensamma tangenter bildar en kon, som har sin spets i papprets plan. Spetsen är då även skärningspunkten för de ursprungliga två linjerna.

Men om det finns tre kulor, så är det inte bara så att alla kan läggas på ett papper, vi kan lägga ett plant papper ovanpå dem också! Det pappret tangerar alla kloten, och det har lika mycket rätt att innehålla konspetsarna som det undre planet hade.

Således finns konspetsarna, det vill sägga de erhållna tre punkterna i båda planen. Och två plan skär varandra i en linje! Alltså ligger punkterna på en och samma linje.

Nu kan vi alltså glömma bort hela tredje dimensionen-grejen. Vi har visat att de tre punkterna ligger på samma linje i det tvådimensionella planet.

Här kan ni även titta på en film som illustrerar lösningen.

Etikett: dimension

Måla kubens yta

Måla kubens yta

Bollvolymer i n dimensioner

Klassiska bevis: Monges sats