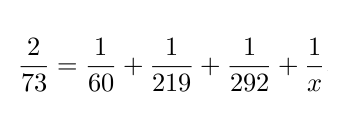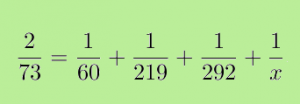Det är sällan som nya matematiska upptäckter handlar om någonting enkelt. All matematik som lärs ut i grundskolan upptäcktes för länge sedan av gamla greker, araber, kineser och indier. Gymnasiematematiken baserar sig på upptäckter som är minst 300 år gamla. Den nyaste forskningen är även för svår för universitetsmatten: algebrakurser har exempelvis varit ungefär likadana sedan 1920-talet.
Just därför är det så imponerande när nya enkla samband hittas. Calkin och Wilf publicerade en artikel om följande struktur så sent som 2000. Likt Pascals oändliga triangel, introducerar de ett oändligt träd, med nu är noderna bråktal.
Börja med att skriva 1/1 högst upp.
Sedan upprepa samma process om och om igen: om ett tal a/b är med i trädet, rita ut två grenar från det och skriv bråket a/(a+b) i den vänstra grenen och (a+b)/b i den högra. Till exempel, så kommer 1/1 att förgrenas i 1/2 samt 2/1.
1/2 kommer att förgrenas i 1/3 samt 3/2, och så vidare. Vi får följande struktur, som bär namnet Calkin Wilf-trädet:
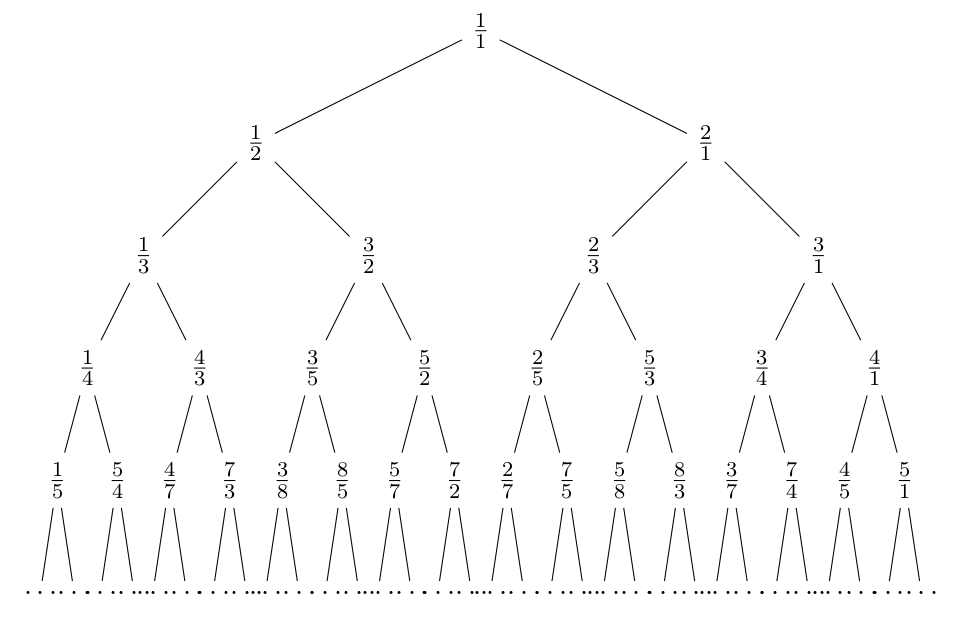
Låt oss skriva ner bråken genom att läsa av en rad i trädet i taget. Vi får listan:
Notera att varje bråks nämnare sammanfaller med nästa bråks täljare. Varför är det alltid så?
För två grannar i trädet är egenskapen inte alls konstig, eftersom båda talen sammanfaller med a+b. Men om två tal är bredvid varandra i trädet utan att vara omedelbara grannar, så är det ena någons högergranne, medan det andra någons vänstergranne. Notera att högergrannar alltid ärver nämnaren, medan vänstergrannar ärver täljaren. Om vi följer arvet upp i trädet från våra två tal, kommer vi till slut fram till två tal, som faktiskt är omedelbara grannar, och därför är det första talets nämnare lika med andra talet täljare.
I den allra sista situationen är två tal grannar i raden, men i trädet skedde en radbrytningen mellan det första och det andra talet. Men vi ser att alla tal i slutet av raderna har nämnare 1, medan alla i början av raderna har täljare 1, så egenskapen bevaras här också.
Bråkraden har även andra egenskaper. Kan du komma på några?