Mattegåta
En springare hoppar alltid på schackbrädet antingen två rutor vågrätt och en ruta lodrätt eller tvärtom.
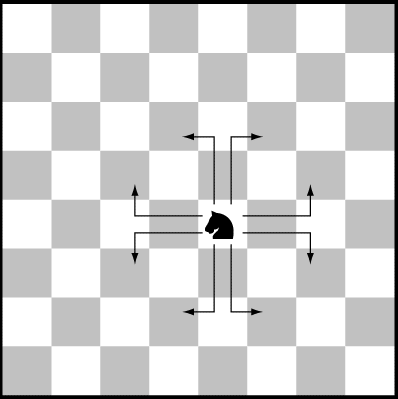
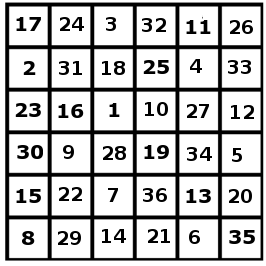
Plötsligt kom en ond schackspelare och placerade springaren på ett litet 6×6-bräde. Då började springaren hoppa frenetiskt mellan rutorna. Här syns spåren efter hoppandet.
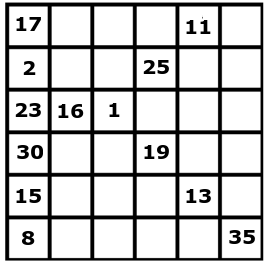
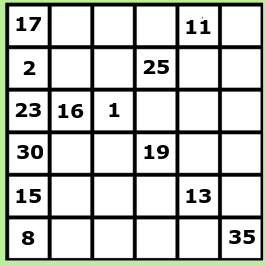
Det visade sig, att springaren var på varje ruta exakt en gång. Den började på ruta nummer 1. Återställ alla nummer upp till 36 som saknas.
Diskussion
För att bestämma lösningen kan man börja med hörnen. Till exempel så står det 17 i övre vänstra hörnet, vilket betyder att de enda rutorna som springaren når därifrån är 16 och 18. Därför kan man sätta ut 18 redan nu.
Resten av siffrorna kan vi inte vara säkra på direkt. Det man kan göra är att skriva in alla möjliga versioner på var till exempel siffran 3 kan vara. Efter det skirver vi in alla möjliga versionen på siffran 4 (från alla möjligheter för siffran 3). Vi fortsätter att sätta ut möjligheter för 5, 6 och 7. När vi senare kommer till en siffra som redan finns (som 8), kan vi sudda bort några av möjligheterna.
Ibland blir det för många möjligheter och då får man göra observationer på några andra tal (var kan talen 34 och 36 finnas?) På slutet är det faktiskt bara en möjlig väg som är kvar och det är den här.
Lösning