Finalresultat
För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla uppgifter!
På delad andraplats kom två Lundabor också, nämligen Anna-Lisa Rathsman och Hugo Eberhard. Hela resultatlistan kan du se på HMT:s hemsida.

Finalproblemen
Prova att lösa uppgifterna själv!
1. Lotta väljer slumpmässigt två olika tal bland talen 1, 2, 3, 4, 5, 6, 7, 8 och 9. Hon beräknar därefter deras produkt. Hur stor är sannolikheten att produkten är ett ensiffrigt tal?
2. Parken Parc des Mathématiques är formad som ett kvadratiskt rutnät med 5×5 trädgårdar. Två trädgårdar anses vara grannar om de har en gemensam sida (men inte om de bara har ett gemensamt hörn). Om man placerar en vakt i en trädgård så kan den vakta den parterren samt alla grannar.
a) Placera ut sju vakter i parken så att alla 25 trädgårdarna är vaktade.
b) Visa att det inte går att vakta hela parken med fem vakter.
3. I kvadraten ABCD dras fyra linjer: från hörnet A dras en linje till mitten av sidan CD, från B till mitten av sidan AD, från C till mitten av sidan AB och från D till mitten av sidan BC. Hur stor är fyrhörningen som bildas i mitten i förhållande till hela kvadraten?
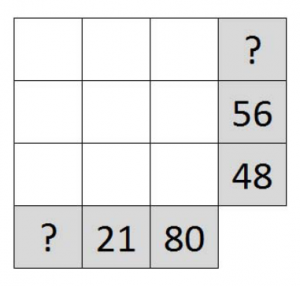
4. I 3×3-rutnätet är vissa radprodukter och kolumnprodukter utsatta. Finn alla möjliga sätt att placera samtliga siffror från 0 till 8 i rutnätet så att produkterna blir korrekta.
5. En oändlig talföljd a1, a2, a3,… har egenskapen att för alla positiva heltal m och n gäller
Vidare vet vi att a3 = 2015. Bestäm a2015.
6. Aladdin önskar sig tre böcker med sagor. Varje bok skall ha två tusen och fjorton sagor. Var och en av sagorna kan vara antingen spännande eller romantisk. Dock kommer hans käresta att ta en av böckerna eftersom hon också vill läsa sagor.
Aladdin förklarar för anden att han kommer läsa två sagor varje natt, en från varje bok som han har kvar. Självklart läser han dem i den ordning de står i böckerna. ”Men”, förklarar Aladdin, ”jag vill ha omväxling, så ibland vill jag ha två olika typer av sagor och ibland två lika typer, och jag kräver att vid precis hälften av nätterna få en romantisk och en spännande saga”.
Kan anden ge Aladdin tre böcker så att alla Aladdins önskemål är uppfyllda, oavsett vilken bok hans käresta tar bort?
Statistik
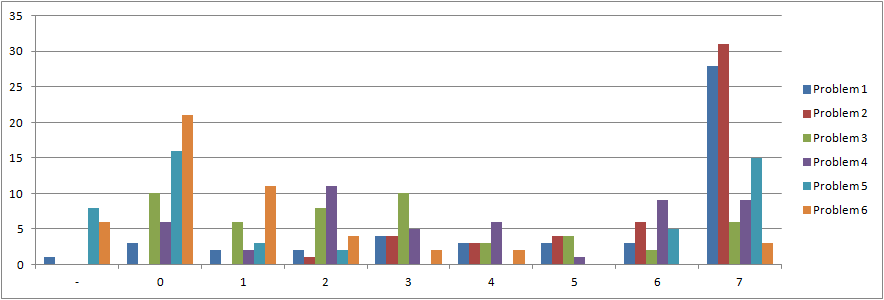
Tävlingen innehöll flera svåra problem. Som mest kan man få 7 poäng på ett problem, men man kan också få delpoäng. Snittresultaten blev sådana:
* Problem 1: 5.18
* Problem 2: 5.98
* Problem 3: 2.76
* Problem 4: 3.70
* Problem 5: 2.64
* Problem 6: 1.08
Så det var problem 2 som var lättast och inte problem 1 som vi i juryn trodde.
På graden kan du också se hur många finalister (y-axeln) som fick ett visst antal poäng på respektive problem.
Arbetet i jurygruppen
I år var jag en av medlemmarna i jurygruppen och hjälpte till att ta fram problemen. Jag tror att juryn kan vara stolta över resultatet, då vi fick en tävling med roliga varierande problem. De flesta av dem innehöll någon twist och det var inte självklart hur man skulle lösa dem. Ändå är de möjliga att lösa eller vad tycker du? Är det något speciellt problem som du tycker är extra snyggt?
Själv gillar jag problem nummer 6 väldigt mycket. Från början hade den en annan formulering:
”Aladdin önskar sig ett rutnät med 2014 rader och 3 kolumner, där varje ruta är färgad antingen turkos eller gredelin. Han önskar sig specifikt ett rutnät som är sådant att vilka två kolumner han än väljer så är antalet rader där rutorna i de två kolumnerna har samma färg lika stort som antalet rader där rutorna har olika färg. Går det att uppfylla Aladdins alla önskningar?”
Vi valde att formulera om det till en mer konkret situation med sagoböcker. Olika människor föredrar olika formuleringar, men i slutändan ska det ju inte spela någon roll. Välj vilken formulering du vill och försök lösa Aladdin-problemet!

