Roligare matematik
Nu har alla decembergåtor fått svar!
Jag vill tacka alla läsarna som påpekat oklarheter och felaktigheter i svar. Fortsätt gärna att göra så!
Här är alla adventsgåtorna:
Pappersark
Sifferrebus
Myntpåsar
Läskig sjukdom
Klurigt uttryck
Tom och Jerry
Tändstickor
Påståenden
Defekt pixel
Fisken
Möjliga kuber
Kannibalernas tidspress
Annorlunda luffarschack
Finurligt tal
Möbelfabriken
Ett parti schack
Magiska cirklar
Ett meddelande
Mattekorsord
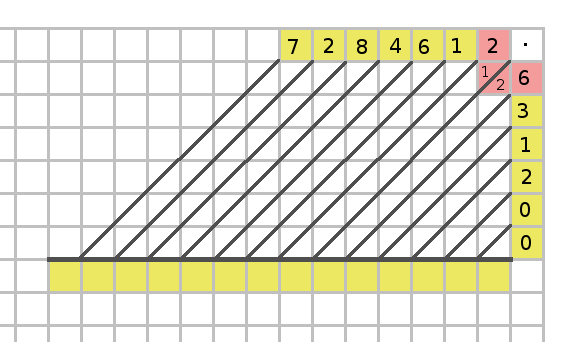
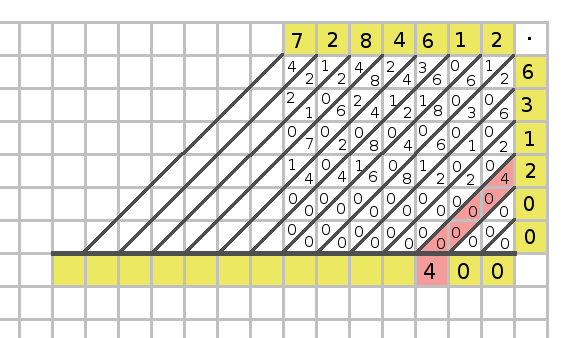
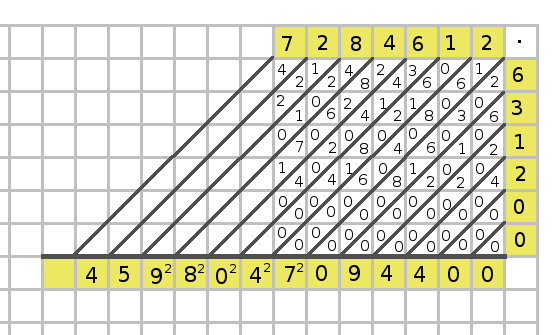
I lördags genomfördes den årliga finalen av Högstadiets Matematiktävling, där Sveriges 44 bästa högstadieelever deltog. Jag var på plats i min gamla gymnasieskola (Danderyds Gymnasium) och såg bl.a. på prisutdelningen.
Jag vill säga ett stort grattis till vinnarna Emma Johansen, Lars Åström och Lisa Lokteva från Linköping, Limhamn och Borås respektive, som allihopa fick fullpoäng! Ett extra grattis till bloggtävlingens vinnare Toomas Liiv, som kom sjua!
Vanligtvis är jag med och rättar deltagarnas lösningar, men i år förberedde jag och genomförde en presentation som var ”pausunderhållning”. Presentationen handlar om den matematiska idén ”reduktion”, som går ut på att man reducerar svårare problem till enkla. Det är ganska mycket humor i föredraget samt förklaringar på vad som skiljer en matematiker från andra vetenskapsmän. Lite som i historien om en matematiker och en fysiker i detta inlägg.
Presentationen tar circa 25 minuter och ni som är lärare kan använda den på förslagvis någon lektion i diskret matematik. Låt gärna eleverna diskutera uppgiften om målaren först, innan lösningen avslöjs.
Bläddra genom filen med piltangenterna efter att ha tryckt F5.
En vän tipsade mig om den här fina sagan:
Historian kommer från användaren Vihart på Youtube, som har andra underbara videor. Jag har sett serien ”Doodling in Math” och känt igen mig väldigt mycket :)
Ett nytt år innebär för mig nya sysselsättningar. Vårterminen 2011 blev jag nämligen för första gången en gymnasielärare!
Jag undervisar en grupp elever i matte C på ett gymnasium i Uppsala och det är då andra halvan av kurser som gäller för min del. Men de första veckorna har vi bara repetitionstillfällen, det vill säga vi repeterar den första halvan av kursen.
Till förra lektionen skapade jag min första power point-presentation någonsin (en beamer-presentation egentligen, dvs gjord i LaTeX). Den använde jag dock inte på lektionen, utan planerar istället att modifiera och utöka den lite och använda på det andra repetitionstillfället.
Kika gärna på min lektion nummer 1, som handlade om förenklingar. För att visa filen som en power point-presentation, öppna pdf-filen, tryck på F5 och bläddra medelst mellanslag eller piltangenterna. Skriv gärna vad ni tycker!
En julklapp till er, kära läsare! Ett korsord!
Korstalet hittade jag och min kompisar på när vi gjorde tävlingen Mattekvadraten år 2002. Det var en lagtävling, så tanken är att 4 personer hjälps åt att lösa uppgiften. Skriv gärna ut och lös uppgiften med din familj, eller själv om du tror att det går snabbare så :) GOD JUL!
Fyll i precis som ett vanligt korsord. En siffra finns med från början. Obs! Inga tal börjar med noll.
Vågrätt:
2. Identiskt med lodrätt-3
4. En tvåpotens
6. Ett minsta tvåsiffriga tal som är lika med hälften av en kvadrattal
8. Största femsiffriga talet som har alla siffror olika
9. Vågrätt-6 multiplicerat med lodrätt-12
10. Ett tal som är en kub men inte en kvadrat
11. En trepotens
13. 1112
15. Ett kvadrattal
16. Ett tal som består av siffror 0,1,2,3 och 4 och är delbart med 8
Lodrätt:
1. Arean av en kvadrat med sida 12.
2. Multipel på 22
3. Palindrom (ett tal som ser likadant ut bak och fram)
5. Största tresiffriga talet
7. Palindrom
12. Ett primtal
13. Ett antal timmar på ett helt antal dygn
14. En sjupotens
Ni kanske har hört talats om magiska kvadrater, men nu är det magiska cirklar som gäller.
Fyll i talen 1 till 10 i de små cirklarna, så att summan av talen i varje stor cirkel blir samma.
När Julen närmar sig är det dags att plocka fram brädspelen … Varför inte schack?
Svart gjorde ett drag och efter det såg det ut så här på brädet:
Vad gjorde svart för drag och vad gjort vitt för drag innan dess?
Tre kandidater till jobbet på en möbelfabrik fick en uppgift på intervjun. De fick beskriva hur man avgör huruvida en bordskiva är formad som en kvadrat eller inte.
Den första kandidaten föreslog att man skulle jämföra bordskivans sidor med varandra, den andra tyckte att man skulle mäta diagonalerna och se ifall de var lika, den tredje tyckte däremot att man skulle jämföra de fyra strecken som bildas då diagonalerna skär varandra.
Vem av kandidaterna har störst chans att få jobbet?
Min elev Erik har lärt mig hur man multiplicerade stora tal på medeltiden. Uppställningen påminner om hur vi gör nu, men talens enskilda siffror multipliceras i en tabell.
Skriv upp två tal som du vill multiplicera, ena som vanligt från vänster till höger, det andra uppifrån och ned, och gör diagonala streck som på bilden. Produkten ska skrivas in i rutorna längst ner.
Varje siffra i första talet ska multipliceras med varje siffra i det andra talet. Resultatet skrivs in i rutan som motsvarar kolonnen för första siffran och raden för andra.
Om resultatet är till exempel 2*3=6 så skrivs 0 in i vänstra halvan av rutan och 6 i högra. Man behöver egentligen inte skriva in nollor.
Nu är alla multiplikationer gjorda och det är dags att addera!
Det är därför vi hade sneda linjer, det är längs med dem vi ska addera! Till exempel blir den tredje sneda summan lika med 4.
Vi fortsätter att addera från höger till vänster och ibland blir det minnessiffror (i det här exemplet råkade alla minnessiffror vara lika med 2).
Min elev tyckte att det här var det bästa sättet att multiplicera och att han framöver bara skulle utföra sådana här multiplikation!
Vilken multiplikationssätt tycker du bäst om?
© 2009-2024 Mattebloggen
.