Denna höst har jag börjat jobba på ett helt nytt sätt. Jag undervisar fem- och sexåringar i matte i ryska klubben ”Kolobok” i Stockholm! En gång i veckan träffar jag fyra grupper med barn mellan (en med femåringar, två med sexåringar och en med tioåringar) och håller ungefär 40 minuter långa lektioner med dem på ryska (lektionerna ska delvis stimulera hemspråksinlärning).
Egentligen kallas våra lektioner för ”logiskt tänkande” och de flesta skulle inte kalla det vi gör för ”matte”. Men uppgifterna och aktiviteterna jag hittar kommer direkt från pedagoger som kallat sin verksamhet för ”matte för barn”.
Jag måste erkänna att jag aldrig har varit lärare för så pass små barn förut. Att hålla 7 stycken sexåringars intresse för en uppgift samtidigt är inte det lättaste som finns. Lägg på lite språkbarriärer då vissa av barnen inte förstår så mycket ryska. Recept för katastrof, eller? Helt illa har det ändå inte gått och jag vill gärna dela med mig om vilka aktiviteter som har funkat och vilka inte har funkat för barnen och varför.
Så vad har vi gjort på träffarna? Nedan kommer de viktigaste aktiviteterna jag genomförde för de minsta barnen under mina första två träffar med dem.
Barn och grafer
”Barn och grafer” är en bok av Frédérique Papy och Georges Papy som jag hoppas skulle passa mina småttingar. Den handlar om förskolelektioner som genomfördes i Frankrike. Lektionerna gick ut på att barnen skulle bekanta sig med olika sätt att representera objekt och reationer mellan dem (punkter och pilar), ett sätt att rita det hela på är med hjälp av grafer. Jag kommer ihåg att jag själv tyckte om boken som liten, men inte riktigt hur gammal jag var när jag kunde förstå det boken hadlade om.
Hur som helst tänkte jag testa att ha samma sorts lektioner med mina barngrupper. Första lektionen började med att vi pratade om syskon. Jag frågade barnen ifall de hade syskon och hur gamla syskonen var och det hade de flesta av barnen inga problem att svara på. Ett av barnen hade en bror som var 70 år tror jag :)
Sedan lade jag fram en stor bild med punkter och sa att punkterna var barn. Några av barnen hade inga problem med att räkna till femton. Men när jag sedan frågade vilka av barnen var flickor och vilka var pojkar istället för skratt (som det stod i min referenslitteratur) fick jag seriösa förslag på vilken punkt som var vem och av vilket kön.
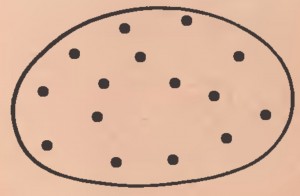
När jag frågade hur man skulle rita att varje barn pekade på sin syster var det bara i en grupp som ett av barnen föreslog pil som notation. Vi ritade lite pilar (många barn kunde rita hyfsade pilar, men inte alla), men bilden jag visade efter gav verkligen inte väntade resultat.
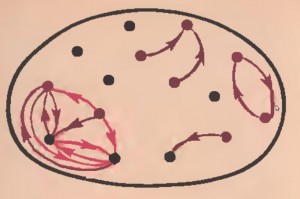
När jag nu frågade vilka barn som var flickor och vilka var pojkar fick jag svar på grund av frägen på punkterna och pilarna verkade ignoreras. Mina förklaringar om hur det egentligen låg till gav inga resultat så jag lade ner projektet. Det var nog alldeles för tidigt för dem att hålla på med grafer och därför inte så kul.
De märkte för övrigt att jag hade kvar muspekaren på en utskriven bild och undrade vad den gjorde där. Kanske är det en bra idé att ha stora bilder som man lägger fram och som alla barnen får peka på och rita i, men just de här uppgifterna var inte passande. Jag lägger boken på hyllan och eventuellt tar fram den senare.
Läsa berättelse
En till ”mattebok” ur min tidiga barndom. De är en rysk bok som egentligen är en saga, som handlar om två vänner: Tomatik och Kubarik. Handlingen är ett spännande äventyr som egentligen passar för barn mellan 3 och 6 år, men boekn är också väldigt pedagogisk. Allt eftersom introducerar begrepp som ”många”, ”ingen”, ”längd”, ”jämförelse” och så vidare som en naturlig del av berättelsen. För de flesta sexåringar är inga av begreppen nya, men just för mina kan det vara bra att de lär sig alla dessa ord på ryska.
När jag läste var det dock svårt att se vilka barn som lyssnade och vilka som tänkte på annat. Under olika träffar har jag försökt göra läsningen mer interaktivt och pekat i boken och ställt frågor, vilka flera av barnen gärna svarar på och då tycker att läsningen blir roligare. Ändå har jag valt att bara fortsätta läsa berättelsen för min grupp med femåringar. De andra har inte saknat berättelsen (jag läste för dem bara första träffen). En av femåringarna hörde jag däremot säga ”Kubarik är rolig” trots att det knappt har hänt nånting i boken hittills. Vännerna har städat och ritat och jämfört vem som haft längst tåg och längst järnväg. Kubarik är för övrigt en häst som Tomatik har byggt av kuber för att han ville ha en kompis.
Färgkoden
I somras köpte jag ett par pussel från Smart Games. Ett av dem heter ”Color code” och går ut på att man ska lösa pussel genom att kombinera olika färgbrickor (brickorna ska läggas på varandra och ovanifrån ska det se ut som på en bild i boken.) Det bästa är att det finns 4 svårghetsnivåer, så de flesta människor, inte vara barn, kan hitta en uppgift som är lite utmanande för dem.
Alla barnen ville göra en uppgift åtminstone en gång, vissa tänkte snabbt och ville verkligen hjälpa de andra. Några av barnen tvärtom sabbade för andra och gömde bitar. Allt som allt var det en lyckad aktivitet som vi återvände till när vi hade gått igenom allt planerat. Alla klarade av de problemen de fick. Jag hade med spelet både första och andra träffen.
Gissa och räkna antalet steg från en vägg till en annan (genomfördes bara med sexåringar)
Precis som det låter, det kändes som att barnen behövde röra på sig, så jag hittade på aktiviteten på plats (egentligen läste jag om någon som har genomfört denna aktivitet och att det har varit lyckat). Barnen tyckte att det var väldigt kul att gå från ena väggen till andra och räkna samtidigt. När jag gick med väldigt stoora steg och fick totalt få steg, förstod de att det blir färre steg då man går stort. Men de kunde inte säga rätt på frågan om vem som har flest steg direkt, eftersom begreppen “större antal” och “större steg” blandades ihop. Kanske berodde det på språkbarriären. Sedan började barnen springa okontrollerat under uppgiften ibland, hitta fler väggar etc. För några tog räkningen slut vid ex. 10 steg, eftersom de helt enkelt inte hade lärt sig räkna till mer.
Pilar
Som sidospår på ”barn och grafer” (se ovan) bad jag dem att rita pilar. Några ville rita många, några ville inte rita någon pil alls (om de fick en dålig (gul) penna). Sedan pratade vi om klockor (visare heter precis som pilar på ryska) och jag bad dem rita klockor. De flesta gjorde bra imitationer och kunde säga hur många visare deras klockor hade, men väldigt många gjorde spegelvända siffror av någon anledning. Det förvånade mig att det var fler som ritade spegelvända än rättvända siffror. Beror det på att de titta på klockan i spegeln eller är det bara en slump? Ofta skriver ju barn bokstäver spegelvänt till exempel.
Vi pratade sedan lite om klockor i allmänhet. Barnen kunde berätta om vad för form deras klockor hade (kvadrat, cirkel och till och med hjärta). Jag bad dem att göra läxa: titta på klockan hemma och rita av den så bra som möjligt. Bara ett barn tog med sig en ritning nästa gång, och då hade bilden alla möjliga klockor på sig. Det var nästan alla de hade hemma, vilket var typ 10 stycken! Kanske ska jag vara mer tydlig med läxan och ge den skriftligt (eller en helt en bild som de ska göra något med, det viktigaste är att de fysiskt får läxan och inte bara verbalt.)
Klockor
Till andra träffen tillverkade jag en klocka med bara timvisaren. Jag ställde in den på olika siffror och frågade varje barn en egen fråga ”vad är klockan?”. Alla kunde svara rätt. När jag sedan ställde in visaren precis mellan 6 och 7 blev det svårare. I en av gruppen tyckte någon att klockan var då 7, men när jag berättade för dem att det var snarare ”6 och lite till” kunde de svara på liknande frågor själva. Det här momenten kräver nogrann förklaring och tålamod när diskussionen sker. Väldigt synd för övrigt att vi inte kan ha så stora disskussioner eftersom många av barnen känner sig osäkra på språket.
Så småningom ska jag introducera minutvisaren, men det är nog för tidigt än. Först borde nog alla barnen lära sig att räkna till tolv.
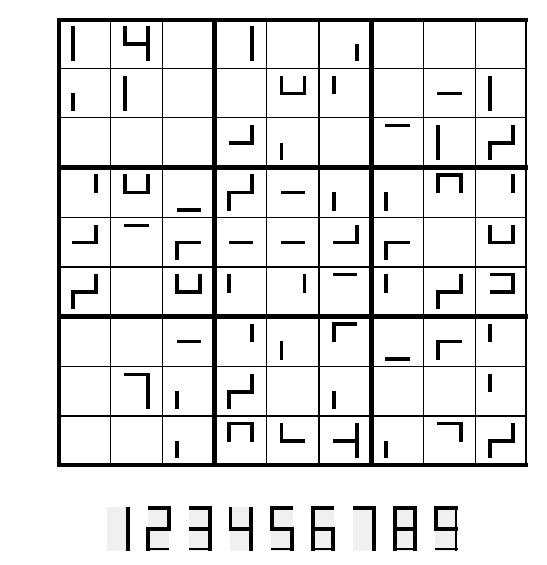
Minisudoku
Alla barn fick var sin uppgift där de skulle fylla i en figur som saknas. Sådana här uppgifter brukar förekomma på IQ-tester, men egentligen är det bara en minisudoku med 3 siffror (3 sorts objekt). Bäst gick det i sexåringsgruppen där jag tog mig tid att förklara vad mönstret gick ut på. Jag hade färre deltagare då och kunde ha en diskussion om varför de ville rita en eller annan figur. Många föreslog fel figur fler gånger.
Några av barnen fick en liknande uppgift till och sedan en uppgift där 4 figurer av 9 saknades och man skulle komplettera mönstret. Alla de här uppgifterna var intressant nog mycket svårare för femåringar än för sexåringar. De som klarade uppgifterna fort och så att säga ”förstod mönstret” var lite besserwissers mot andra och sade att uppgiften var ”lätt”. Ett av barnen tyckte att det var en stjärna som saknades i rutan och ville absolut rita en varpå ett annat barn började rita ett eget mönster från en tom lapp med stjärnor, ovaler och rektanglar istället för de vanliga figurerna. Tyvärr blev det ett fel i det mönstret.
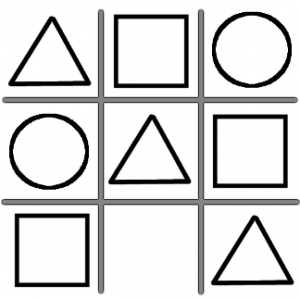
Mosaik
En stor del av andra träffen gick ut på att bygga bilder med mosaik. Jag har ett stort förråd med bitar som tar upp en halv ruta (trianglar), en ruta (cirklar och kvadrater) och två rutor (rektanglar) i olika färger som man kan fästa vid en platta och få till någon snygg bild eller mönster.
Uppgiften jag gav till de två första grupperna var att i par bygga två likadana figurer. Tanken var att de skulle hitta på något mönster tillsammans, men då de överhuvudtaget gick med på den här ”tävlingen” var det så att ena barnet dominerade och det andra försökte kopiera. I den sista gruppen gav jag istället uppgiften att bygga en symmetrisk bild (spegelsymmetrisk), vilket de flesta klarade någorlunda. Några barn försvann i sin egen värld och byggde helt enkelt det de ville bygga. Jag märker att många av barnen tycker om att rita och bygga med mosaik så det måste vi göra mer.
I överlag så tror jag att aktiviteterna har varit uppskattade, men jag behöver hitta på fler inför varje lektion, då barnen kan tröttna ganska snabbt eller rentav rata en aktivitet direkt. Fler kreativa uppgifter behövs och fler uppgifter då barnen ska röra på sig fysiskt.
Har du tips eller synpunkter, kommentera gärna. Jag försöker inte lära ut något specifikt förutom logiskt tänkande och resonerande egentligen, så alla sorts aktiviteter är välkomna!