Spel och pyssel – Sida 4

Adventspyssel 12

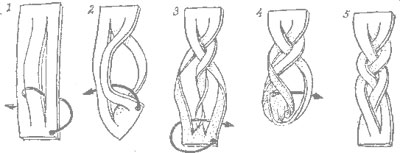
När Johan Björklund såg inlägget om flätan tipsade han mig om följande konstruktion. Snyggt och smaskigt tycker jag!

Hur man skär en bagel i två länkade halvor

Det är inte så svårt att skära en bagel i två likada halvor, länkade till varandra som två länkar i en kedja.

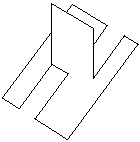
Det första steget är att sätta ut eller visualisera fyra viktiga punkter. Om du lägger bageln framför dig, är A en av punkterna högst upp (på högersidan i mitten). B är en punkt på hålets ”cirkel” (rakt framför dig), C är en av punkterna som nuddar bordet (i mitten på den vänstra sidan), D är punkten närmast dig.

De punkterade linjerna gör det lättare att sätta ut de viktiga punkterna, de behövs egentligen inte för att skära.

Rita en slät kurva ABCDA genom alla punkterna som börjar och slutar i punkten A. Det är längs med den linjen du ska skära. Du kommer att skära runt bageln på två sätt samtidigt: både runt den stora cirkeln (ringen som utgör själva bageln) och runt bagelns ”tjocklek”.

Den röda linjen är precis som den svarta, men vriden 180 grader. Det bästa vore att sätta kniven i den svarta linjen så att den kommer ut på den röda linjen. Men det är lättare att sätta in kniven både i svarta och i röda linjen och skära till hälften på varje linje.

Efter skärningen kan halvorna flyttas isär, men de är fortfarande ihoplänkade som i en kedja!

Förutom att det är roliga att skära så här, får man äta mer ost, eftersom arean för pålägget blir större!

Bilderna och texten kommer från George W. Hart, gå in på sidan för mer info och problem om bageln. Han skriver bland annat för Museum of Mathematics.

Adventspyssel 5

Varje dag innan Jul kommer det publiceras en lite gåta eller något pyssel, och ni kära läsare får gärna skicka in egna bidrag till valentina.chapovalova@gmail.com!

Sierpenskis triangel

Mycket vacker konst kan göras av fraktaler. Nedan har man börjat konstruera Sierpenskis triangel, och det kommer ta låång tid att få den klart :)

sierpinski_lera

Bilden hittade jag på sidan Evil Mad Scientist.

Adventspyssel 4

Varje dag innan Jul kommer det publiceras en lite gåta eller något pyssel, och ni kära läsare får gärna skicka in egna bidrag till valentina.chapovalova@gmail.com!

Idag är det ingen gåta, utan ett pyssel.

Magisk fläta

Läder (som fått mjukna upp i exempelvis vatten) fungerar tydligen bra som material för att fläta remmar som sitter ihop. Följ det här schemat:

Själv provade jag med en pappersbit och misslyckades totalt! Är det någon som lyckats göra flätan?

Adventspyssel 1

Pappersark

Klipp ut en sådan här figur ur en A4:

Visa svaret

Lösningen till problemet för de yngre vecka 43

Mattegåta

Tre vänner har ett företag ihop. Deras efternamn är Eriksson, Karlsson och Nilsson. En av dem är VD, en är sekreterare och en är kassör. Sekreteraren har inga syskon och han är den yngste på företaget. Nilsson är äldre än kassören och är gift med Erikssons syster.

Bestäm VD:ns, sekreterarens och kassörens respektive efternamn.

Diskussion

Problemet är ett typiskt exempel på en mysteriegåta. Det kanske inte är särskilt stor mystik över vem som verkligen är VD på företaget, men det är i vilket fall okänt för oss.

Om du inte vet var du ska börja, rita en tabell över alla möjligheter:

Målet att vi ska välja exakt en ruta i varje rad och varje kolonn. Då kommer precis en person bli kassör, en sekreterare och en VD.

Men först måste några rutor uteslutas.Till exempel sekreterare-Eriksson-rutan (tänk på varför).

Fortsätter du på detta vis får du fram vilka rutor som är fel och vilka som är rätt. Lösningen med svaret finns längst ner.

Gillar du sådana här problem rekommenderar jag ett beroendeframkallande spel Sherlock – The Game of Logic. På sidan kan ni ladda ner ett demo och prova att spela.

Spelet går ut på sammaställa en unik person med en unik frukt, ett hus, en siffra och lite andra grejer. Till sin hjälp har man massa olika ledtrådar på den högra sidan av skärmen. De kan säga vilka saker som finns bredvid varandra (till exempel kolumnen med R måste vara bredvid kolumnen med det röda huset), ifall något är till vänster om något annat, ifall tre saker inte ligger efter varandra (åt något håll). Det finns alltid en unik lösning på slutet!

Lösning (av Toomas Liiv)

Sekreteraren har inga syskon och är yngst. Nilsson är äldre än kassören och kan därför inte vara yngst. Nilsson är gift med Erikssons syster. Eriksson har alltså minst ett syskon. Sekreterarens kriterier passar inte in på vare sig Eriksson eller Nilsson och måste därför vara Karlsson.

Nilsson är äldre än kassören och kan därför inte vara kassör, förutsatt att han inte är äldre än sig själv. Den enda kvarvarande möjligheten är VD, vilket han då också måste vara.

Kvar finns Eriksson och kassören som då måste vara samma person.

Alltså har vi att:

• VD:ns namn är Nilsson

• Sekreterarens namn är Karlsson

• Kassörens Eriksson

Planära grafer

I ett sällskap med många personer kan man leka en lek som kallas ”knuten”. Alla ställer sig i en ring och sluter ögonen. Sedan sträcker alla fram båda sina händer och börjar gå mot mitten. Alla ska ta tag i två andra händer med sina egna.

Efter att alla är klara med det öppnar man ögonen. Målet är nu att lösa upp ”knuten” som bildats utan att släppa taget med händerna. Det gäller att bilda en stor ring igen (det kan också hända att det blir flera ringar).

Ett liknande spel är Planarity, fast personerna i spelet kan ha fler än två händer. Målet är att lösa upp all tilltrassel så att inga par av händer måste hållas över varandra.

Personer är representerade med punkter och en kant som går mellan två punkter visar att de två personerna håller handen. Alla spelande har väldigt uttänjbara händer. Försök att klara några nivåer! (Jag kom till Level 7.)

Sådana här bilder kallas grafer, om de går att ”plana ut” på det här snygga sättet (så att inga två kanter korsar varandra) kallas de planära. Det är svårt att se direkt huruvida en graf är planär eller inte, däremot uppfyller alla planära grafer följande formel.

Eulers formel

En graf är ritad på ett plan på så sätt, att inga två kanter korsar varandra. Om V är antalet hörn i grafen, E – antalet kanter och F – antalet områden som planet delas upp i, så gäller:

V – E + F = 2

Att det blev just talet 2 beror på att man ritade på ett plan. Ritar man grafer på andra konstiga ytor blir det ett annat specifikt tal just för denna yta. Det talet kallas ytans eulerkaraktäristik.

Roliga mattelänkar

Här är lite mattejulpyssel:

Crazy paper thing

Förvisso har jag sett videon innan, men återupptäckte den igår på Let’s Play Math!, en trevligt matteblogg på engelska.

Kenken och set

För den som tröttnat på Sudoku och Battleships vill jag föreslå ett par andra pussel.

Den första är kenken, ett spel som självaste Gunnar Berg spenderar timmar med! Till synes liknar pusslet sudoku, men man får inte lika många siffror utsatta från början. Det gäller att fylla tabellen så att siffrorna inom varje rad respektive kolonn är olika (siffrorna skall vara från 1 till tabellens storlek). Dessutom skall olikaformade rutor ge ett visst resultat med given operation. Står det 15+ till exempel, så ska siffrornas summa i området vara 15.

Det pusslet är lite roligare än sudoku tycker jag. Man får öva på lite fler tekniker. Det bästa man kan göra för att lösa pusslet är att tillämpa den så kallade flaskhalsprincipen. Man börjar med den platsen, där det finns så få möjligheter som möjligt. Till exempel, står det 4x i ett område innehållande två rutor, så vet man att talens produkt skall vara lika med 4. Men eftersom de står på samma rad/kolonn så är enda möjligeten talen 1 och 4 (men man vet inte än i vilken ordning de kommer). Man lär sig lite om olika sådana exempel för varje aritmetisk operation. Prova på själv!

Den andra spelet är Set, som i original pappersversion kan spelas med flera personer. Det gäller så snabbt som möjligt att hitta en trippel med kort som följer regeln ”allt lika eller allt olika”. Alltså varje egenskap som korten kan ha (färg, form, antal, fyllning) ska den i en set antingen vara lika för alla kort eller vara olika för alla kort. En annan tumregel är: ”om två är något, men inte den tredje, så är det inte ett set”. Det brukar vara svårt att hitta ett set i början, men efter ett tag utvecklar man ett sorts ”seende” och kan snabbt hitta de rätta korten. Spelet passar exakt lika bra för vuxna som barn.