karta

Pizzasats nummer 2

Matematik används inte bara när man ska skära upp pizza, utan också när man ska äta den. Möjligen har ni löst problemet nedan utan att ens tänka på matte.

När en pizzabit tas ut ur kartongen ser det ofta ut så här:
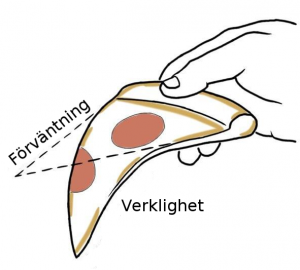
förväntning

Mot detta finns följande strategi:

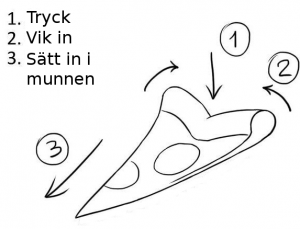
Men varför fungerar det? Det hela beror på en sats som Gauss kom på.
gauss

Gauss sats har att göra med att alla ytor har så kallad krökning. Det är ett mått på hur mycket objekt kan böja sig utan att deras ”materiella” struktur förstörs (fler exempel på detta kommer senare).

Varje naturlig kurva har en specifik böjningsradie r i varje punkt. Storheten 1/r kallar vi då för krökningen i den punkten. Om kurvan är rak kring punkten, så säger vi att böjningsradien är oändligt stor och krökningen är lika med 0.

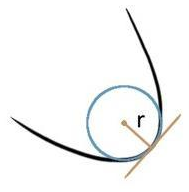
krökning

Samma definition gäller för ytor, men nu har punkten många olika värden på krökningen – en i varje riktning. Det maximala samt det minimala värdet av krökningen för en punkt kallas för huvudkrökningar.

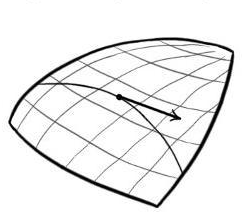
kurvatur_yta

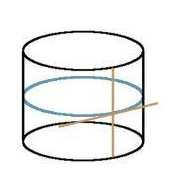
TIll exempel, på ett plan har alla punkter alltid krökning 0, medan på en sfär med radie R har alla punkter överallt krökningen 1/R. En cylinder med radien R kommer ha huvudkrökningarna lika med 1/R respektive 0.

kurvatur_cylinder

Om vi böjer lite på ett A4-papper, så kommer inte avstånden mellan punkterna på pappret att förändras. Sådana ändringar av ytor kallas isometrier.

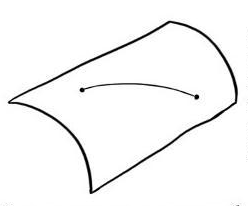
papper

Om vi rullar ihop pappret, kommer vissa punkter ha ett kortare avstånd mellan sig än tidigare, eftersom nu finns det vägar som går genom kortsidorna som nu nuddar varandra.

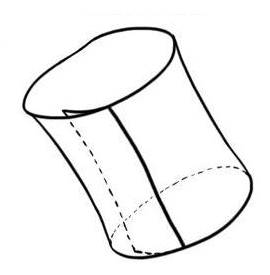
papper_rulle

Gauss underbara sats (Theorema Egregium) säger att vid en lokal isometri kommer inte ytans Gaussiska krökning (produkten av huvudkrökningarna) att förändras.

Så länge pizzabiten ligger i kartongen är alla dess krökningar lika med 0.

pizzabit_kurvatur

Så fort pizzabiten tas ut, kommer den att böja sig. Då kommer ena huvudkrökningen att växa, medan den andra förblir 0.

pizza_sned_kurvatur

Men om kanterna viks upp kommer den sistnämnda huvudkrökningen sluta vara 0. Men enligt Gauss sats ska produkten av huvudkrökningarna förbli noll, det vill säga den andra huvukrökningen måste bli 0.

pizza_upp_kurvatur

Pizzabiten rätar ut sig och går bra att äta!

(Bilderna är tagna ur ryska internet, källa okänd. Tack konstnären!)

Theorema Egregium förklarar varför vi inte kan omforma ett papper till en boll utan att skrynkla ihop det. Inte heller kan en boll slätas ut till en sfär.

Det mest kända exemplet på detta är kartor. Jorden kan inte få en platt karta utan att avstånd förvrängs. Testa ett kartpussel för att övertyga dig om detta.

En lektion för små barn i grafteori

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.

Här kan du se vad vi tidigare har gått igenom.

Grafer

Jag försökte att introducera grafer på den allra första lektionen men begreppen tog sig inte. Det var inte naturligt för fem- och sexåringarna att representera människor med prickar och syskonsrelationer med pilar. Eller så passade inte temat till att vara först av alla helt enkelt.

Därför tänkte jag prova igen att bekanta barnen med grafer, denna gång med en mycket mjukare introduktion. Därför handlar egentligen inte så stor del av lektionen om grafer.

Barn ska kunna differensiera enkla linjära former

Titelt är ett skämt och betyder ungefär att barn ska kunna skilja på cirklar, trianglar och kvadrater.

Dagens lek går ut på att bygga ett land som består av öar. Öarna har alla olika färg och form: cirkel, rektangel, ring, femhörning etc. Barnen ska kunna nämna alla formerna. Vi placerar öarna på ett stort blått papper som symboliserar havet.

Broar

För att öarna ska bilda ett rike, måste det finnas sätt att ta sig emellan dem. Barnen får en bro i taget (en platt avlång rektangel), som kan förbinda två öar med varandra. Vilket är det minsta antalet broar som behövs för att man ska kunna promenera runt hela landet?

När vi har byggt det minsta antalet broar som krävs för att landet skall vara sammanhängande (vilket är 1 mindre än antalet öar). Hur många broar till kan vi bygga, om inte två broar får korsa varandra (broarna får vara böjda)? På den sista frågan vet inte jag det exakta svaret. Tillsammans med barnen ska vi i alla fall hitta ett lokalt maximum, det vill säga en situation där ingen ny bro kan sättas in, hur den än slingrar sig, på grund av korsandet av andra broar.

Köningsbergs broar

Man bestämde sig för att måla om alla broarna i landet till en ny färg. Går det att köra med målarbilen exakt en gång på varje bro? Det vill säga aldrig köra på en och samma bro två gånger och inte heller utelämna någon bro.

Barnen får göra minst ett försök var. Det tar ett tag innan man hittar den rätta vägen, om den nu existerar!

Detta är samma problem som Köningsbergs broar. Bara formulerat lite annorlunda.

Rita utan att lyfta pennan

För de äldre barnen passar uppgiften: rita figuren utan att lyfta pennan från pappret medan du ritar.

Auktion

Varje barn får ett och samma antal pappersmynt. De får i hemlighet bjuda ett visst antal mynt på varje ö. Den som bjuder flest mynt, får bli öns president (om det är lika, bjuder man om). Mynten man har kvar, kan man spendera på byggblock, som man får bygga presidentpalatset av på sin ö.

Detta lär barnen hur en bjudning kan fungera. Också lär de sig att snabbare jämföra antal och avgöra vem som bjöd flest mynt.

Det är dags att rita landets karta! Rita av landet på ditt eget papper. Du kan börja med ön där du är president och rita resten därifrån.

Samtidigt som barnen ritar jag en ”karta” där öar bara är prickar och broar är streck. Sedan får barnen se kartan. Kan alla peka på sin egen prick?

Flaggor

Landets färger är blått (havets färg), gult (solens färg) och rött (broarnas färg). Vi vill att landet inte bara ska ha en flagga, utan alla möjliga randiga flaggor som består utav 1, 2 eller 3 ränder!

Barnen får tillsammans måla alla flaggorna och kontrollera att de ha tagit alla kombinationer. Eventuellt kommer de på att man kan ha ränderna på det andra hållet (som i den rumänska flaggan och inte den ryska). Om ränderna är som på bilden ovan, finns det 15 olika flaggor man kan göra.

Set

Om det blir tid över, spelar vi set med de äldre barnen. På spelet står det att lägsta åldern är 6, men jag tror att det är meningsfullt att köra spelet först vid 7.

Lösningen till problemet för de äldre vecka 45

Mattegåta

Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.

Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)

Diskussion

Eftersom det frågas efter det minsta antalet i uppgiften är det underförstått att resultat skall bevisas. Det vill säga det måste finnas ett exempel med x bollar (om x är svaret), samt bevis för att det inte går med färre än x bollar.

Ett sätt att jobba på är att börja underifrån (till exempel med 1 eller 2 bollar) och för varje antal antingen visa att det inte går eller att det går. Fallen är oftast svårare närmast svaret. Lite som i fyrfärgsproblemet!

Fyrfärgsteoremet

Sats. För en platt ”karta” räcker det alltid med fyra färger för att måla ”länderna” på kartan så att inga två länder med gemensam gräns har samma färg (gränser utgörs av raka eller krokiga linjesegment).

Det var länge känt att det räckte med fem färger och att det finns kartor som inte går att färga med tre färger. Men fallet fyra tog lång tid tills den äntligen bevisades med hjälp av datorberäkningar.

Lösning (av Erik Svensson)

Till att börja med kan vi uppenbart utesluta att det går med bara en boll (och förstås även med noll bollar).

Det finns ej heller någon lösning för två bollar, ty vi vet att två bollar (punkter) entydigt bestämmer en linje, så om samtliga hål ska ligga i linje med två bollar, då måste alla hålen ligga på samma linje. Men hålen på biljardbordet ligger inte på en linje.

Det är inte heller möjligt med tre bollar, vilket vi ser om vi försöker konstruera en. Om vi har tre bollar, då finns det två möjligheter: Att de ligger på en linje eller att de inte gör det.

Ifall de ligger på en linje, då får vi en motsägelse med samma resonemang som för två bollar, och ifall de inte ligger på en linje så bildar de en triangel. I så fall utgör varje linje med två bollar en sida i denna triangel, och bollarna är hörnen.

Vi börjar med att konstatera att ingen sida i denna triangel kan täcka tre hål, ty de enda linjerna på bordet som täcker tre hål är långsidorna. Ens om vi antar att frågeformuleringen tillåter bollar längs med sidorna innebär detta att två bollar måste ligga på en av långsidorna, vilket innebär att den tredje bollen måste ge upphov till två linjer som täcker samtliga tre resterande hål, vilket medför att någon av dessa två linjer måste täcka två hål på den andra långsidan och ändå korsa den första långsidan, vilket är omöjligt.

Att täcka fyra eller fler hål med en linje är förstås också omöjligt som biljardbordet är uppbyggt.

En linje kan ej heller passera genom bara ett hål, eftersom detta lämnar fem hål att täckas med de resterande två linjerna, och alltså måste någon av dessa linjer täcka minst tre hål, vilket motsäger det vi just kom fram till. Även en linje som inte täcker några hål kan vi utesluta, eftersom denna linje i så fall kan tas bort och därmed ge en lösning för två hål, vilket vi visat inte existerar.

Således måste vi ha tre linjer som täcker exakt två hål, och de måste täcka två bollar vardera. Eftersom varje boll är ett hörn i den triangel som bildas ligger varje boll på två sådana linjer.

På bilden ser vi alla möjliga linjer som täcker två hål, samt alla skärningspunkter mellan dem. Dessa punkter är de enda kandidaterna till var en boll kan ligga. Vi ser emellertid att det inte finns någon triangel av sådana punkter (med de utmarkerade linjerna som sidor), och den minsta slutna figur vi kan bilda är en fyrhörning. Alltså finns det ingen lösning för tre bollar, men det finns en för fyra, till exempel genom att välja fyra punkter som bildar en fyrhörning i bilden och lägga bollarna där.