Fem punkter på avstånd
[kkratings]
På ett papper finns fem punkter, som är betecknade A, B, C, D och E. Avståndet AC (dvs avståndet mellan punkten A och punkten C) är 5 cm, avståndet AE är 4 cm, BC = 14 cm, BD = 2 cm, DE = 3cm. Hur långt är det mellan mittpunkterna på sträckorna AB och CD?
Matteproblem för de äldre vecka 45
Mattegåta
Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.
Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)
Lösningen till problemet för de äldre vecka 38
Mattegåta
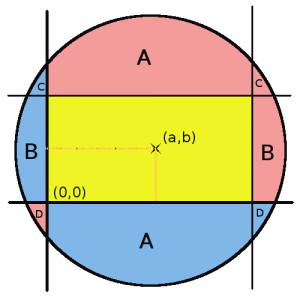
En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.
Om S+ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S+-S– lika med?
Diskussion
När problem handlar om att jämföra areor, så är det ofta så att delar av de här areorna är lika, speciellt när delarna har konstiga former (jämför med problemet för de yngre vecka 35).
Börja med att rita den enklare varianten (då cirkelns mitt är i första kvadranten) och försök att ta bort så många lika stora delar från S+ och S– som möjligt och jämför det som blir kvar.
Lösning (av Johan Björklund, något modifierad)
Jag tillför två hjälplinjer paralella med koordinataxlarna genom (2a,2b). De är spegelbilder av koordinataxlarna speglade genom linjer (igenom parallella med koordinataxlar) genom (a,b).
Det är lätt att se att flera av områdena har lika area (markerat med bokstäver). De kommer att ta ut varandra när vi beräknar S+-S– (S+ är den gula plus den rosa arean, medan S– är den gula plus den blå). Kvar blir den centrala rektangeln med area 4ab.
Tillägg (av Erik Svensson)
Detta var ifall mittpunkten låg i den första kvadranten. Om den istället ligger i den tredje kvadranten, då är fallet uppenbart det samma efter rotation med ett halvt varv, och ifall mittpunkten ligger i andra eller fjärde kvadranten, då speglar vi i y- respektive x-axeln och får samma fall fast med S+ och S- ombytt, så att den sökta arean byter tecken.
Vi finner emellertid att just 2a * 2b ändå uttrycker arean i samtliga dessa fall.
Matteproblem för de äldre vecka 38
Mattegåta
En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.
Om S+ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S+-S– lika med?
Matteproblem för de yngre vecka 35
Mattegåta
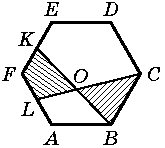
Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs med BK och sedan längs med LC. Hanna fick den triangulära biten BOC, medan Sofie fick den fyrkantiga biten KOLF. Vilken tjej fick mer tårta?