Rekommenderad från: 12 år
[kkratings]
En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika). Bestäm det minsta möjliga antalet rum i en sådan lägenhet.
Två fyrkanter
Rekommenderad från: 12 år
[kkratings]
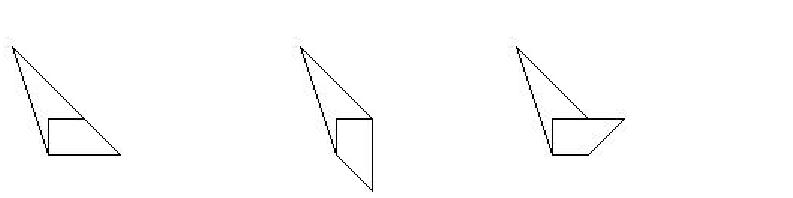
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med ”läggas ihop” menas att fyrkanterna inte får överlappa varandra, inte heller får det bildas hål.
Bläckfiskarna
Rekommenderad från: 12 år
I havet bor många olika bläckfiskar. Om en bläckfisk har ett jämnt antal armar så talar den alltid sanning, men om den har udda anta armar så ljuger den alltid. En gång sade den gröna bläckfisken till den mörkblåa:
– Jag har 8 armar. Och du har bara 6.
Då blev den mörkblåa sur:
– Det är jag som har 8 armar. Du har bara 7.
Den svarta bläckfisken höll med:
– Den mörkblåa har verkligen 8 armar. Men jag har hela 9!
Varpå den randiga bläckfisken sade:
– Det är ingen av er som har 8 armar! Bara jag har 8.
Vilka bläckfiskar hade exakt 8 armar?
Kvartscirkel
Rekommenderad från: 15 år
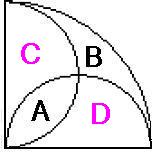
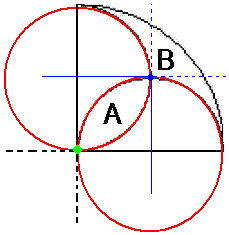
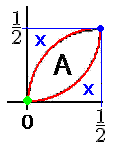
Från början har vi en kvartscirkel med radie 1 cm. Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.
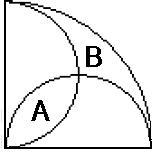
i) Hur förhåller sig areorna A och B?
ii) Vad är areorna A och B lika med?
Kvadratuppdelning
Rekommenderad från: 12 år
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med ”att dela upp” menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.
Hjärtfigur
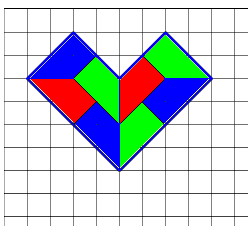
Rekommenderad från: 10 år
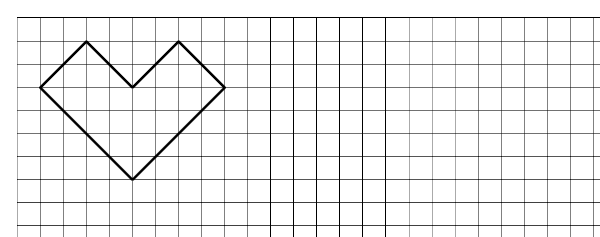
Dela upp hjärtfiguren nedan i 8 likadana delar. Delarna räknas som likadana om de har samma form och storlek (de kan dock vara placerade på olika sätt).
Blåröda tallinjen
Rekommenderad från: 15 år
Förkunskaper: intervall, tallinjen, delbarhet, potenser.
På reella tallinjen markerade Johan alla kvadrater på positiva heltal. Varje erhållet intervall delade han sedan i två lika stora delar, de vänstra halvorna målade han blått (inklusive vänstra änden), medan de högra målade han rött (exklusive högra änden).

1. Visa att för varje positivt heltal n kan han hitta ett blått tal som är delbart med talet n.
2. Visa att för varje positivt heltal n kan han hitta ett rött tal som är delbart med talet n.
3. Visa att Johan kan hitta 1000 olika positiva heltal, så att summan av vilka som helst 5 av dem är ett rött tal.
4. Visa att det finns oändligt många röda tal som är potenser av två.
Parkering
Rekommenderad från: 10 år
[kkratings]
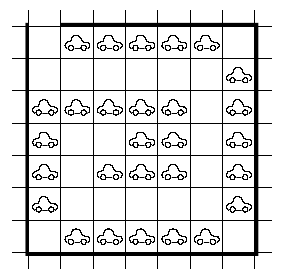
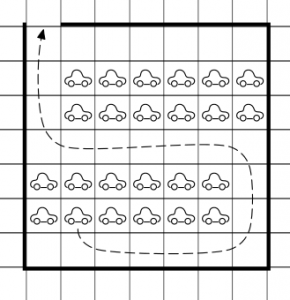
I staden Bilköping finns en parkering med plats för 7×7 bilar. Man kan komma in endast genom porten, resten av parkeringsplatsen är omsluten med staket. En vakt vill parkera så många bilar som möjligt, men så att varje bil kan komma ut samtidigt som alla de andra står stilla. På bilden lyckades han göra så med 24 bilar.
Försök att placera ut så många bilar som möjligt!
© 2009-2024 Mattebloggen