Etikett: randvinkelsatsen

Öva på geometri inför SMT-kval

Kvalomgången i Skolornas matematiktävling sker imorgon. Om du vill fräscha upp era geometrikunskaper inför tävlingen
här står det korfattat vad du behöver plugga på. Notera att minst ett av problemen på tävlingen är ett klassiskt geometriproblem.

Tyvärr har de flesta deltagare nackdelen att inte ha gått igenom så mycket geometri i skolan. Har man övat på geometriproblem åtminstone några gånger, har man en stor fördel där, eftersom geometriproblemen är inte särskilt svåra (de algebraiska problemen på SMT kräver oftast fler icke-triviala insikter).

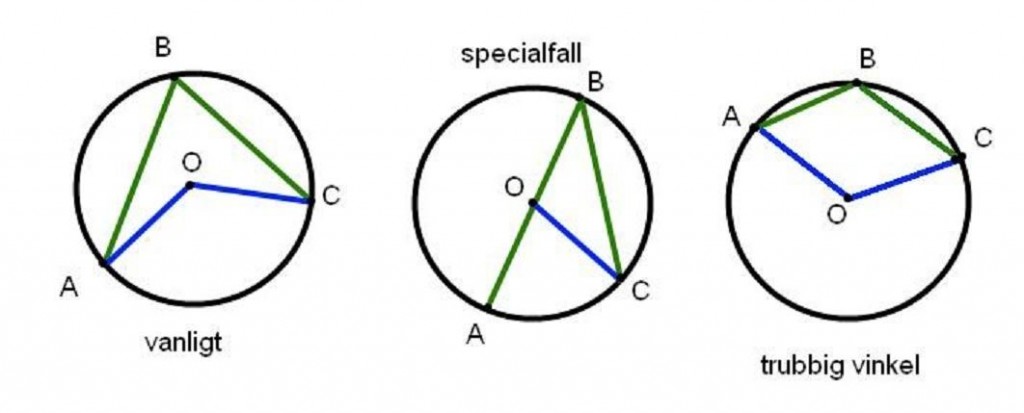
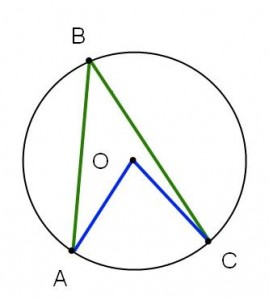
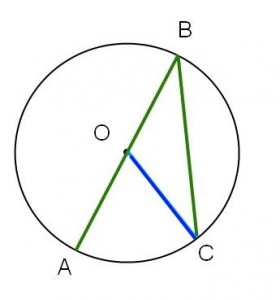
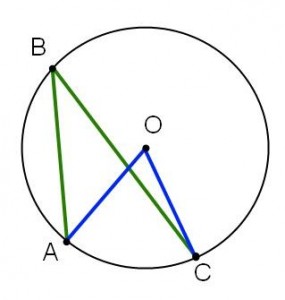
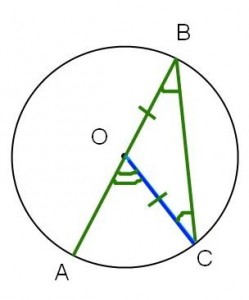
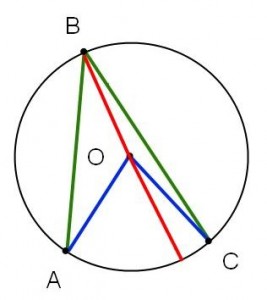
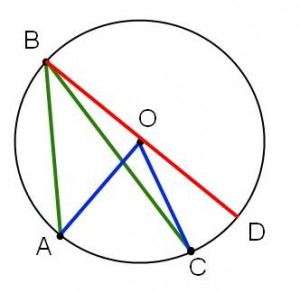
Några användbara geometrisatser har jag samlat i en cirkellektion i geometri. Vi pratade om följder av randvinkelsatsen och användningen utav dessa följder i problem om figurer som kan skrivas in i cirklar.

Kan du göra rätt på övningarna samt på de första fem problemen så har du fått hum om hur geometriproblem skall bevisas. Då kan du gå över till de svårare problem, som jag har hämtat från riktiga SMT-kvalomgångar. Notera dock att lektionen inte täcker geometriska tekniker som likformighet, areor, samt sinus- och cosinussatsen. Det finns så pass mycket användbar geometri, så att det inte får plats i enda lektion.

Lycka till på tävlingen! Skriv gärna i kommentarerna hur det har gått för dig och om tipsen har hjälpt :)

Klassiska bevis: Randvinkelsatsen

Många har hört talas om den beryktade randvinkelsatsen. Eventuellt har du träffat på den på gymnasiet. Men få har egentligen koll på hur man bevisar satsen.

Om du vill komma fram till beviset själv med hjälp av några ledande uppgifter, se Cirklar och randvinklar. Annars läs vidare här.

Sats (Randvinkelsatsen)

Markera tre olika punkter A, B och C på en cirkel. Markera även cirkelns mittpunkt O. Då är vinkeln AOC dubblet så stor som vinkeln ABC.

Bevis

Man ska vara väldigt försiktig och rigorös med geometriska bevis. Med det menas att alla möjligheter för bildens utseende ska undersökas, om man nu ska rita någon bild överhuvudtaget.

Så till exempel, kan det se ut så här:

Så hur ska man täcka alla möjligheterna på ett bra sätt? Det beror förstås på vad man tänker baser beviset på.

Oftast betraktas bilderna som väsentligen olika om olika skärningar mellan linjerna äger rum. I bevisen grundar vi ofta resonemang på hur olika objekt ligger i förhållande till varandra och inte så mycket på storlekarna på vinklar, cirkelbågarna etc.

Med detta sagt väljer vi således att betrakta tre fall (som täcker alla möjliga situationer):

Fall I Fall II Fall III

Fall I: Vinkel AOC ligger helt inuti vinkeln ABC.
Fall II: Detta är specialfallet då vinkeln AOC delar sida med vinkeln ABC.
Fall III: Två av vinklarnas sidor skär varandra.

Fall II

Detta fall verkar vara enklast, så vi börjar med det. OB=BC för att de är radier, så \triangle COB är likbent. Alltså gäller \angle OBC = \angle OCB.

\angle AOC + \angle BOC = 180\textdegree men också \angle OBC + \angle OCB + \angle BOC = 180\textdegree.
Då måste \angle AOC = \angle OBC + \angle OCB = 2\angle OBC. Vilket skulle bevisas.

Fall I

Första fallet då? Vi ”fuskar lite” och drar en hjälplinje. Men nu får vi egentligen Fall II igen! Tillämpa det på varje halva av bilden och addera.

Fall III

Fall III måste väl vara svårare? Inte då! Vi ”fuskar” och drar en hjälplinje igen. Vi får återigen på grund av Fall II att 2\angle DBA=\angle DOA och att 2\angle DBC=\angle DOC. Subtrahera det andra resultatet från det första och vi är klara!

© 2009-2024 Mattebloggen