IMO – Mattebloggen

Sista dagen för att anmäla dig till matematik-SM!

Nu är det snart igång igen! Sverige väljer sina skarpaste hjärnor bland gymnsieeleverna för att i sommar skicka de 6 bästa till matematik-VM eller IMO, som det egentligen heter. Jag blev imponerad av de senaste resultaten, då Sverige tog hem en silvermedalj! Det händer inte så ofta tyvärr.

Sista anmälningsdagen är 14 september. Jag har för mig att även högstadieelever kan få lov och delta. Jag skulle tro att mattebloggens läsare absolut har en chans att lösa ett par problem (av sex stycken). Dock kräver några av problemen ofta kunskaper som man får i tvåan eller trean på gymnasiet, så tävlingen är mer riktad på de sistnämnda. Men jag tycker att man ska känna på tävlingen även om man är yngre.

Här är lite info från den officiella hemsidan:

Den 27 september tävlar gymnasieskolor runt om i landet i Skolornas matematiktävling (även kallat matematik-SM). Tävlingen har arrangerats av den ideella föreningen Svenska matematikersamfundet sedan 1961 och firar i år 50 årsjubileum. Det är den äldsta tävlingen i matematik och naturvetenskapliga ämnen för gymnasieskolan. Förra året deltog 126 skolor runt om i landet i tävlingen.

Skolornas matematiktävling är ett av flera kvalificerande moment till deltagande i den ansedda Internationella matematikolympiaden (IMO). I juli i år arrangerades IMO 52:a gången 12-24 juli i Amsterdam. Sverige kom på plats 54 av 101 deltagande länder, en klar förbättring mot i fjol då Sverige hamnade på plats 72. Nästa matematikolympiad arrangeras i Argentina i juli 2012.

Uppdatering: Tips om vad man kan ”plugga på” innan tävlingen.

Problem vecka 21

Matchen (2 poäng).
Innan fotbollsmatchen mellan lag Syd och lag Nord fanns det 5 prognoser:
a) det kommer inte att bli oavgjort
b) Syd kommer att släppa in mål
c) Nord kommer att vinna
d) Nord kommer inte att förlora
e) det kommer bli exakt 3 mål i matchen

Efter matchen visade det sig att exakt tre prognoser stämde. Vad blev matchens resultat?

Dvärgarna (4 poäng).
Draken fångade sex dvärgar, låste in dem i sin grotta och sade till dem: ”Jag har sju hattar som har var sin färg: röd, orange, gul, grön, blå, lila och vit. Imorgon vid gryningen kommer jag att binda för era ögon och sätta var sin hatt på er och en hatt gömmer jag. Efter det kommer ni att kunna se, men ni får inte längre prata med varandra. Sedan får var och en viska till mig, vilken färg det är som saknas. Om åtminstone tre stycken gissar rätt, befrias ni alla. Om färre gissar rätt, äter jag upp er alla.”

Vad ska dvärgarna bestämma innan gryningen, för att rädda sig själva?

Rutnätet (6 poäng).
Varje punkt med heltalskoordinater på planet målades i en av tre färger. Visa att det går att hitta en likbent rätvinklig triangel med hörn i punkter med heltalskoordinater, som är målade i samma färg.

Visa lösningar

Matchen (Oves lösning):
Om Nord vinner då är a),b),c) och d) sanna.
Om det är oavgjort så är a), c) och e) falska (då tre mål ej kan fås vid oavgjort).
Alltså eftersom att exakt 3 ska vara sanna, måste Syd vinna, eftersom ingen av de andra fallen fungerar.

Så Syd släpper in mål och det görs exakt 3 mål i matchen och Syd vinner, så då måste det bli 2-1 till Syd.

Dvärgarna (Davids lösning):
Varje dvärg ser alla färger utom sin egen och den som saknas. Av de två färger man inte ser säger man den som vinner. Vilken vinner då?

Röd vinner över orange, gul och grön.
Orange vinner över gul, grön och blå.
Gul vinner över grön, blå och lila.
Grön vinner över blå, lila och vit.
Blå vinner över lila, vit och röd.
Lila vinner över vit, röd och orange.
Vit vinner över röd, orange och gul.

Oavsett vilken färg som saknas så vinner den över exakt tre av dvärgarnas färger. Alltså kommer exakt tre dvärgar säga rätt färg.

Rutnätet
Om vi kollar på en kvadrat med sidan 4 punkter (bestående av 16 punkter), måste två av punkterna på dess diagonal ha samma färg.

Det finns ändligt många sätt att färglägga med sidan 4 punkter med 3 färger, så det finns ett m, som är större än det antalet. Det vill säga, en kvadrat bestående av m^2 kvadrater med sidan 4 har två exakt likadant färgade kvadrater på sin diagnoal (här består diagonalen av kvadrater med sida 4). De stora kvadratens sida består av 4m punkter.

På samma sätt hittar vi en ännu större kvadrat K, som har två likadant färgade kvadrater med sidan 4m på diagonalen.

Antag att det inte finns några rätvinkliga likbenta trianglar med hörnen i samma färg. Vår kvadrat med sidan 4m som har två likadant färglagda små kvadrater på diagonalen har följaktligen 4 punkter med färg ett, 2 punkter med färg två och således 1 punkt av färg tre som kan ses på bilden.

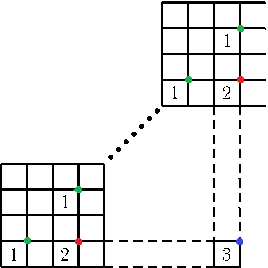
På samma sätt tittar vi på kvadraten K, som då måste ha en ruta, som varken kan ha färg ett, färg två eller färg tre. Motsägelse, alltså måste vi någonstans ha en likbent rätvinklig triangel med hörnen färgade i samma färg.

Problem vecka 20

Cthulhu (1 poäng).
”Ni alledels för små för att se detta”, sade Cthulhu till sina 33 barn och skrek ut ”Blunda!”. Alla pojkarna blundade med högerögat, likaså en tredjedel av flickorna. Alla flickorna blundade med vänsterögat, likaså en tredjedel av pojkarna. Hur många barn såg ändå det som de var för små för att se?

Tabellen (3 poäng).
En 4×4-tabell är fylld med talen från 1 till 16. I varje rad, varje kolonn och varje diagonal (inklusive diagonalerna som består av en ruta) är det största talet markerat. Ett och samma tal kan alltså bli markerat flera gånger. Kunde det bli så att
a) alla tal utom två blev markerade?
b) alla tal utom ett blev markerade?
c) alla tal blev markerade?

Stenhögarna (5 poäng).
Det finns tre stenhögar. Sisyfos rullar en sten i taget från en hög till en annan. För varje sten han överför får han ett antal guldmynt från Zeus, som är lika med skillnaden mellan antalet stenar i målhögen och antalet stenar i starthögen (stenen, som rullas mellan högarna, räknas inte in). Om skillnaden är negativ, lämnar Sisyfos tillbaka en respektive summa till Zeus. Om Sisyfos inte kan betala, låter den välvillige Zeus honom att vara skyldig pengarna.

En gång blev det så att alla stenarna hamnade i samma högar, som de fanns i från början. Hur mycket kunde Sisyfos som mest ha tjänat då?

Visa lösningar

Cthulhu (Toomas lösning):
Vi kan notera att en tredjedel av barnen blundade med båda ögonen, det vill säga 33/3=11 stycken. Antalet barn som ändå såg den givna händelsen var då 33-11=22.

Tabellen (Lisas lösning):
Alla tal kan aldrig bli markerade. För att ettan ska kunna bli markerad måste den finnas i ett hörn för att bli störst i diagonalen på en ruta. Det innebär att även tvåan måste befinna sig i en hörnruta. Detta leder i sin tur att även trean måste vara det eftersom den annars aldrig kan befinna sig i en rad, kolumn eller diagonal där den är störst. Samma gäller fyran. Därefter, var man än placerar femman så kommer den aldrig kunna vara störst i sin rad, kolumn/diagonal eftersom det varje ledig rad/kolumn/diagonal finns plats för fler tal.

Alla utom ett tal kan bli markerade. Det har jag visat genom genom ifyllning av tabellen nedan. Jag lät femman vara utan markeringar och fyllde i resterande siffror på så sätt att varje nytt tal (större än det före detta ifyllda) fick bli störst i en rad, kolumn eller diagonal.

Alla utom två tal kan också bli markerade. Det har jag visat i tabellen nedan. Jag fyllde i rutorna på samma sätt som ovan, men såg först till att placera sexan i en rad/kolumn/diagonal där den inte skulle kunna vara störst.

Svar: a) Ja. b) Ja. c) Nej.

Stenhögarna (Davids lösning):
Istället för att säga att han får betalt med skillnaden så säger vi så här: när han flyttar en sten från en hög måste han betala lika många guldmynt som det finns stenar kvar i högen han flyttade från. När han flyttar en sten till en hög får han betalt med lika många guldmynt som det redan fanns stenar i högen han flyttade till. Detta blir samma sak, men ett lite annorlunda sätt att se på saken. Betrakta nu en given hög med stenar och alla överföringar som görs till eller från den högen. Varje gång en sten flyttas därifrån får Sisyfos betala, varje gång en sten flyttas dit får han betalt. Vi vet att det finns lika många stenar i högen i vår slutsituation som det fanns när vi började. Jag vill visa att den totala summan pengar som Sisyfos har tjänat på den givna högen alltid är 0.

Det räcker att visa att påståendet gäller för första gången han återvänder till lika många stenar som det fanns från början. Om det alltid gäller att han tjänat 0 vid första gången han återvänder, så måste det även gälla för alla gånger efter det: han måste ha tjänat 0 mellan första och andra gången, mellan andra och tredje gången o.s.v.

Vidare räcker det enligt samma resonemang att visa att påståendet gäller för första gången han återvänder till något läge som han redan befunnit sig i. Alltså att första gången som det finns två olika tidpunkter då det finns lika många stenar, så har han tjänat 0 mellan dessa två tidpunkter. Om vi kan visa det så kan vi helt bortse från tiden som förflutit mellan dessa två tidpunkter och inse att det måste gälla även nästa gång och nästa och nästa…

Men första gången han återvänder till ett tidigare läge kan endast ske på två sätt:
a) först tar han bort en sten från högen och därefter lägger han till en sten i högen.
b) först lägger han till en sten i högen och därefter tar han bort en sten från högen.

Låt det finnas x stenar i högen. I a) får han då först betala x-1 och därefter får han betalt x-1. I b) får han först betalt x och därefter får han betala x. I båda fallen blir summan 0 vilket skulle visas.

Vi har nu visat att han för varje hög har tjänat exakt 0. Därför är den totala summan som han tjänat för alla högar också exakt 0.

Inför IMO 2010

imo Härmed vill jag gratulera min mattecirkelelev, Benjamin Fayyazuddin-Ljungberg, för att han har blivit utvald till det svenska laget i tävlingsmatematik!

Tillsammans med 5 andra gymnasister kommer han att representera Sverige i den 51:a Internationella Matematikolympiaden (IMO) i Kazakhstan. IMO är en årlig tävling för hela världens ungdomar och går ut på att eleverna ska lösa 6 problem under två tävlingsdagar. Det är då rätt så svåra problem, här kan ni se förra årets.

Det är riktigt roligt att ännu en av mina elever har blivit utvald till en av de 6 bästa i Sverige. Jag önskar honom lycka till på tävlingen (och jag kommer träna honom inför den så mycket som möjligt)!