Matteklubben har haft lektioner för grupperna åk 2-4, åk 5-6 och sist ut var högstadieeleverna, åk 7-9.
Denna gång kom en hanterbar mängd elever, 25 stycken. Det är ganska lagom för den åldern, nackdelen med för många elever är att någon som är blyg inte törs föra fram sin talan. Jag tror att det kommer bli bättre med det när eleverna har lärt känna varandra lite. I framtiden kanske vi kommer blanda om dem och få dem att jobba lag, men under lektionerna jobbade de antingen själva eller grupper om 2-3, så som det föreföll naturligt för dem.
Vi var fem lärare och de flesta stunderna fanns det någon som inte var upptagen och som eleverna kunde fråga om det var något de undrade.
Blandade problem
Vi började med en timme med blandade kluringar (precis som i åk 5-6). Eleverna fick lösa dem i par och sedan berätta lösningar för oss när de var redo. Problemet var att nästan ingen räckte upp handen. Men när en lärare väl kom fram till en godtyckligt grupp elever så hade de nästan säkerligen löst en eller två stycken kluringar. Stor skillnad där mot yngre årskurser, kanske för att äldre barn redan har vant sig att de inte får uppmärksammad lärartid när de har presterat.
Kluringarna var inte helt självklara för alla, även om de flesta kunde klara av många av dem. Några var inte vana vid den typen av problem och då kunde man lätt missuppfatta villkoren. När vi kommunicerade med eleverna försökte vi fostra matematiskt tänkande hos dem med hjälp av följande frågor.
1. Går det att sätta in en av symbolerna +, -, *, / i varje mellanrum och sedan sätta ut
parenteser så att resultatet av uträkningen blir exakt 100?
Missuppfattningar/funderingar: Några förstod tvetydigheten som att man bara kunde använda sig av samma symbol (det vill säga välja en av symbolerna +, -, *, / och sedan bara sätta ut den). Någon glömde bort att man kan sätta ut parenteser. Vissa misstänkte att det inte gick att göra, men visste inte hur de skulle kunna förklara det.
Frågor/ledtrådar till eleverna: Försök att dela upp 100 i faktorer. Om du har fått en fyra, vad måste du få av resten av tvåorna (eleverna svarar korrekt att det är 25, men sedan måste man inse att det inte går med 25).
2. Piraterna A, B och C hade följande samtal.
A: ”B har 2 ögon.”
B: ”C har 2 ögon.”
C: ”A har 2 ögon.”
A: ”Vi tre har 2 ögon tillsammans.”
B: ”Vi tre har 3 ögon tillsammans.”
C: ”Vi tre har 4 ögon tillsammans.”
Det visade sig att var och en av piraterna ljög lika många gånger som han hade ögon. Hur många ögon hade var och en?
Missuppfattningar/funderingar: Eleverna förstod det som att ett svar räckte. Men för en fullständig lösning behövs att man redovisar alla svar eller förklarar varför fler svar, än de angivna, inte finns.
Frågor/ledtrådar till eleverna: När eleverna förklarade hur de tänkte, utgick de från antaganden, t.ex. ”Piraterna har 4 ögon tillsammans”, men sedan inte betraktade fallet då piraterna inte hade det. Då bad vi dem att gå igenom de missade fallen. Det var ganska omfattande och säkerligen missade vi några fall i diskussionen (det är inte helt lätt för läraren att följa), men eleverna fick en övning i logiskt resonerande och falluppdelning.
3. I ett tomt akvarium lade man ner några glaskulor och fyllde upp med vatten. När man sedan plockade ut hälften av kulorna, sänktes vattennivån i akvariet med en tredjedel. Hur mycket kommer vattennivån sjunka om man plockar ut hälften av de kvarvarande kulorna?
Missuppfattningar/funderingar: Många elever räknade ut andelen som vatten kommer sjunka i andra omgången relaterat till hur mycket vatten det fanns från början (d v s en sjättedel). Men det man undrar över är hur mycket vattnet kommer sjunka i förhållande till sitt dåvarande mängd. (Om man skulle säga ”Vattennivån sjönk med en sjättedel”, då skulle man mena något annat än det som händer i uppgiften.) När de räknade och jämförde bråk hade de oftast ”enheterna” i huvudet (det vill säga att 1/6 och 1/2 kunde beteckna andelar av helt olika saker), men då blev man lätt osäker vad ”enheten” för det slutgiltiga svaret blir.
Frågor/ledtrådar till eleverna: Räknar du med andelen av vattennivån i början eller efter första steget? Det man undrar över är det senare, det vill säga, hur stor andel av vatten i mitten av handlingen försvinner?
Om det är svårt att hålla reda på mängderna så kan du rita en bild.
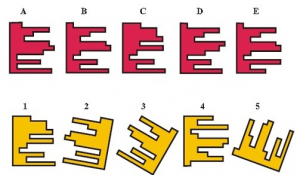
4. En man har ett litet hål i väggen (lika stor som en punkt). Han har också ett märke som han kan hänga upp (se bilden). Markera alla punkter, där han kan sätta spiken, så att hålet täcks av märket.
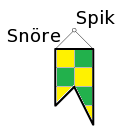
Missuppfattningar/funderingar: Var ligger hålet? Hur stort är det? Här behövdes förklaringen att hålet är lika stort som en punkt och att svaret frågas i förhållande till det utsatta hålet.
Frågor/ledtrådar till eleverna: Markera en punkt. Skulle vi kunna sätta spiken där (markerar en punkt ett steg uppåt från hålet), kommer flaggan täcka hålet då? Vi frågar om några positioner till och eleverna svarar antingen ”ja” eller ”nej”. Vi förklarar att det som frågas efter är helt enkelt figuren som bildas av punkter där man kan sätta spiken. (Eleverna kommer då oftast fram till rätt svar själva.)
Genomgång av blandade problem
Vi lade ner åtminstone 15 minuter på att gå igenom de blandade problemen ordentligt. Eleverna fick presentera olika lösningar på tavlan. Längst tid tog uppgifterna 2 och 3.
På uppgiften om piraterna kom vi tillsammans fram till en uttömmande lösning. Eleverna kom med bra idéer om att utesluta vissa fall av total mängd ögon (t.ex. att piraterna måste ha ljugit minst två gånger på grund av de sista tre utsagorna). De såg också symmetrin i de första tre utsagorna, vilket gjorde att vi inte behövde betrakta tre olika fall hela tiden utan kunde sammanfatta dem (en av de första tre utsagorna är falsk, två av de första tre utsagorna är falska, etc.)
Uppgiften om akvariet var det många som ville förklara hur de tänkte på. Det var bra att öva för eleverna att redovisa inför grupp, eftersom då anstränger man sig extra för att förklara korrekt och tydligt (vilket är en av sakerna man kommer lära sig av att gå på Matteklubbens träffar). Många höll med om att rita en bild på akvariet underlättade lösningen. Några av eleverna satte i konkreta värden (höjd eller volym på akvariet) för att räkna ut svaret, men vi lade inte så mycket vikt vid huruvida det var rätt eller fel att göra. Däremot konstaterade vi (kanske något otydligt just då) att det blir på samma sätt oavsett vilka värden man antar. Det hela handlar om att gå från konkreta och bekanta enheter (cm eller l) till skummare enheter (andelar av totala volymen), vilket är ett svårt steg att ta om man går i sjuan t.ex. Vi kommer att så småningom vänja eleverna vid det generella tanksättet (om de inte redan är vana vid det).
Eftersom det inte fanns så mycket kvar tid till andra halvan av lektionen, ritade vi bara upp svaret på uppgiften om flaggan, men förklarade inte särskilt noga varför det var just svaret. Ska man vara matematiskt petig borde vi ha gjort det, det vill säga visat exakt varför punkterna innanför figuren fungerar som spikplatser och punkterna utanför figuren inte gör det. Däremot förstod eleverna det rätta svaret på ett intuitivt sätt (efter att ha experimenterat).
Delbarhetsprinciper
Dagens tema var delbarhetsprinciper, det vill säga principer och regler för hur man snabbt kan se om ett tal är delbart med något givet annat tal eller inte. Det klassiska exemplet är att man kan se att ett tal är delbart med 2 (d v s jämnt) om den sista siffran är 0, 2, 4, 6 eller 8 (d v s sista siffran är jämn). Detta skrev jag upp som
Jag använde symbolen 
Eleverna kände till fler delbarhetsprinciper och vi skrev upp dem för 5, 3 (och 9) och 4:
![\text{Siffersumman f\](http://l.wordpress.com/latex.php?latex=%5Ctext%7BSiffersumman%20f%5C%22%7Bo%7Dr%20talet%20%7D%20%5Cvdots%203%5Ctext%7B%28resp.%209%29%7D%5CRightarrow%20%5Ctext%7B%20talet%20%7D%20%5Cvdots%203%20%5Ctext%7B%28resp.%209%29%7D%20&bg=FFFFFF&fg=000000&s=0 "\text{Siffersumman f\")
Egentligen gäller påståendet åt andra håller också, och det använde vi under lektionen. Men för att inte förvirra eleverna för mycket med ny notation, använde jag implikationspil (som man ändå fattar som ”pil”) istället för en ekvivalenspil (dubbelpil).
Vi förklarade tillsammans varför delbarhetsprincipen med 4 gäller. Vi delade upp ett konkret stort tal i hundratal och det som blir över (talet som bildas av de två sista siffrorna). Sedan insåg vi att 100 ligger i fyrans tabell och därmed hänger det bara på det sista talet, huruvida det stora talet är delbart med 4. Eleverna förstod beviset.
Många hade tydligen hört några av delbarhetsprinciperna förut, men de flesta kunde inte förklara varför de gällde. De som inte hade bevisat det förut hade även svårare för att komma ihåg dem också under problemlösningsdelen. Så jag tror att det var väldigt nytt och nyttigt med bevis.
Kluringar om delbarhet
Eleverna fick lösa följande kluringar på temat delbarhetsprinciper. Ofta utnyttjade de inte principerna utan kom fram till svar på annat sätt. Men de fick ledtrådar när de hade kört fast och då förstod de hur delbarhetsprinciperna kunde komma till nytta. Följande dialoger kunde ske under diskussionen av respektive uppgift.
1. Skriv en siffra till vänster och en siffra till höger om 10 så att det nya talet blir delbart med 12 (det vill säga blir ett tal där divisionen med 12 går jämnt upp).
Elever: Vi kommer inte fram till något svar.
Lärare: Tänkt på att talet är med 12:ans tabell. Vilka andra tabeller måste talet vara med i?
Elever: Fyrans, sexans, treans…
Lärare: Var vet om tal som är med i fyrans tabell?
Elever citerar delbarhetsprincipen med 4.
Lärare: Och vad vet om tal som är med i treans tabell? Skulle vi kunna kombinera det vi vet för att hitta ett svar?
Elever: Ahaa, smart.
2. Skriv 2014 efter sig själv några gånger så att talet som bildas blir delbart med 9.
Elever: Vi skrev upp 2014 efter varandra och dividerade (vi kunde fortsätta divisionen genom att skriva till några fler 2014) tills det gick jämnt ut.
Lärare: Är det en slump att det blev just 9 stycken?
Elever: Vi skrev upp 2014 efter varandra så att siffersumman blev delbart med 9.
Lärare: Är det en slump att det blev just 9 stycken?
Elever: Nej, siffersumman blir ju 9 gånger siffersumman av 2014.
3. Kan ett tal som bara består av fyror vara delbart med ett tal som bara består av treor? Och tvärtom?
Elever: Vi tror att svaret är ”nej”.
Lärare: Varför det?
Eleverna börjar resonera och kommer fram till att svaret är ”ja” på den första frågan.
Lärare: Och på andra frågan?
Elever: Kanske är svaret ”ja” här också…
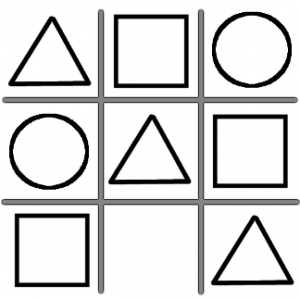
4. I rutorna på en 5×5 står siffror som inte är lika med 0. Av alla raderna och kolonnerna bildas 10 femsiffriga tal. Kan det hända att alla tal utom ett är delbara med 3?
Elever: Kollar man på alla talen?
Lärare: Nej, de som bildas av de 10 raderna (vågräta och lodräta).
Elever: Ja, man kan ha siffror som är delbara med 3 och ändra en av dem.
Lärare: Men då ändrar man två av talen, inte ett.
Elever: Justja…
5. Ett kvadrattal slutar med siffran 6. Visa att den näst sista siffran är udda.
6. Från ett tal subtraherade man talet skrivet baklänges. Visa att resultatet måste vara delbart med 9.
De sista frågorna hann vi knappt, eftersom tiden höll på att ta slut.
Bevis för delbarhetsprincipen med 3
Som exempel tog vi ett större tal och framme på tavlan kom tillsammans fram till att man får siffersumman av talet genom att dra bort tal som är delbara med 3 (för varje tiotal, hundratal, tusental etc. drar man bort ett visst antal 9:or, 99:or, 999:or etc.). Det blev lite oorganiserat på tavlan, så jag vet inte om majoriteten hann förstå beviset. Möjligen borde vi ha gått igenom beviset för talet 9, vilket i stort sett sammanfaller med bevist för 3, men kanske är något självklarare.
Det var kul att träffa intressanta och intresserade högstadieelever! Till vi ses nästa gång, fundera på och diskutera gärna hemmakluringen.
