bevis

Andra träffen med Matteklubben, åk 7-9

Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva som de i åk 2-4, så hade vi lärare inte räckt till. Men som sagt, det var mycket lugnt i klassrummet.

Det är inte så lätt att börja med matematisk problemlösning sent i högstadiet, då man redan har lärt sig en del metoder och hur man brukar göra i matten. Det finns många uppfattningar om hur man bör göra som vi på Matteklubben försöker ändra lite. Det vill säga, vi vill visa dels att man kan göra matte på många olika sätt, dels vill vi lära ut att vara rigorösa i ens tänkande (annars blir det något annat än matte). Det är extra svårt att lära ut något när man ses så sällan!

Det var därför mycket klurigt att välja tema till lektionerna som är lagom svår, men som också är rätt ny för eleverna, där de inte redan har bestämda sätt att göra uppgifterna på. I andra länder är det vanligt att elever stöter på matematisk stringens först när de läser geometri. Samtidigt har vi i Sverige en mattetävling där eleverna presterar sämst just på geometriuppgifterna (mest för att de inte övat på sådana förut). Därför valde jag ”Vinklar” som tema på dagens lektion.

Men jag vill skriva om lektionen som har varit i kronologisk ordning, därför börjar vi med hemuppgiften.

Hemfrågan

Sist i uppgiftsbladet förra gången stod hemuppgiften. Den gick ut på att, med hjälp av att betrakta rester som tiopotenser ger vid division med talet 11, lista ut en delbarhetsprincip för talet 11.

Det var ungefär 3-4 elever som hade tänkt på uppgiften hemma, vilket är glädjande, det betyder att de tyckte att det var tillräckligt intressant och en lagom utmaning. Självklart förväntar jag mig inte att man ska titta på hemuppgiften, då det finns så mycket annat som kallar på ens uppmärksamhet. Men de som tycker att det är kul att utforska ska givetvis göra det, jag försöker att välja lagom uppgifter för det.

Innan vi tog oss an delbarhetsprincipen med 11 och elevernas teorier, repeterade vi beviset för hur man visar att ett tal och dess siffersumma ger samma rest vid division med 9. Mycket för att påminna om hur rester fungerar (att man kan subtrahera tal som är delbara med 9 och få samma rest) men också för att de som var nya på träffen skulle komma in i vad vi höll på med. Jag gjorde en tydligare uppställning än förra gången, då beviset lite hastigt gicks igenom på slutet av lektionen.

Sedan svarade vi på frågorna om vad det blir för rest när man dividerar 100…00 (jämnt antal nollor) med 11 och när man dividerar 100..00 (udda antal nollor) med 11.

I det första fallet tyckte eleverna att svaret var 1, och för att visa det subtraherade vi talet 99..99. Vi diskuterade dels hur många nior det fanns i talet (lika många som nollorna i tiopotensen), dels vad resultatet av divisionen 99..99/11 blir. Eleverna hade inte helt lätt för att svara på den frågan, förmodligen för att de inte är vana vid att jobba med icke-konkreta (stora) tal. Först fick vi svaret 99..9 (en nia mindre), men efter lite rimlighetskontroll förstod de att vi inte hade räknat rätt. En elev formulerade att svaret faktiskt blev 909090..09 (hälften så många nior). Sedan nämnde jag att det ändå inte var så jätteviktigt vad resultatet blev (men att resultatet är ett heltal är en försäkring om att talet verkligen är delbart med 11).

I det andra fallet tyckte vissa elever att svaret fortfarande var 1, men snabbt insåg vi att svaret var 10 (subtraherade talet 999…90 på samma sätt). Hur skulle vi nu kontrollera delbarheten av ett godtyckligt tal med 11?

Likt fallet med delbarhet med 9 gjorde vi ett konkret exempel med ett tal som bestod av några 10000-tal, 1000-tal, 100-tal, tiotal och ental (t.ex. 30000 + 7000 + 400 + 20 + 1). Varannan siffra gav alltså sig själv i rest (3, 4, 1) och varannan gav sig själv gånger tio (70, 20). Vi har förstås en delbarhetsprincip nu (det är bara att räkna ut summan 3 + 70 + 4 + 20 + 1 och se om resultatet är delbart med 11), men den är ju inte särskilt smidigt.

Skulle vi kunna subtrahera något mer, t.ex. från 70? från 20? Vi vill subtrahera något som är delbart med 11 för att inte förändra resten. En elev föreslog talet 66, och vi provade det och fick 4 som svar. Men det är inte självklart hur man från början skulle få den där fyran från siffran sju. På en förfrågning efter andra förslag sade en elev att man kunde subtrahera 77, och då skulle vi få -7 i summan. En annan elev insåg att det var logiskt att ta bort 22 från 20 (och då få -2 i summan). Tillsamman kom vi fram till att resultatet av 3 – 7 + 4 – 2 + 1 skulle ge ett tal med den sökta resten.

Nu bad jag en elev att formulera delbarhetsprincipen med 11, vilket blev att man räknar ut ”varannan siffra plus och varannan minus”. Vi testade slutsatsen på några exempel. På frågan om man skulle börja räkna med minus eller plus nämnde jag att det inte spelade någon roll. Det är inte trivialt varför det spelar någon roll, men jag gav en snabb förklaring om att resultatet blir precis samma, fast med omvänt tecken. Det spelar alltså roll för den exakta resten, men kvittar om vi bara ska bestämma huruvida ett tal är delbart med 11 eller inte.

Det var roligt att tillsammans bevisa den här riktigt svåra delbarhetsprincipen och se att många hängde med. Frågan är om eleverna kan upprepa det på egen hand, när de till exempel förklarar det för någon annan.

Vinklar

Jag valde vinklar som ett avsnitt i geometri, dels för att eleverna redan har mött dem och vet vad det är för något och dels för att många problem i tävlingen HMT handlar om vinklar. Lär man sig tekniken ”vinkeljakt”, det vill säga har vanan att räkna ut vinklar i olika figurer, så kan man komma ganska långt bara på det.

Tyvärr innebar det att eleverna behövde träffa på många nya begrepp på en gång, men jag försökte poängtera att det inte var lika viktigt att lära sig namnet ”alternatvinklar” som att känna till det faktum att sådana vinklar är lika.

Jag ritade upp en bild med två parallella linjer på tavlan, samt en linje som korsar dem. Det bildas många vinklar (åtta), men vilka av dem är lika? Jag tror eleverna redan hade en känsla för det, men det är ju viktigt i geometri att nämna vad som räknas som ett ”vetertaget faktum” (axiom) och vad som inte gör det. Jag pekade på några par vertikalvinklar och sade att de var lika, förklarade vad likbelägna vinklar var (och att det var lika), samt att det då följde att alternatvinklar var lika.

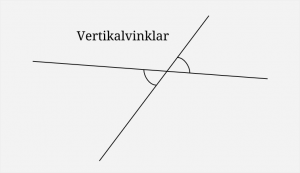
vertikal

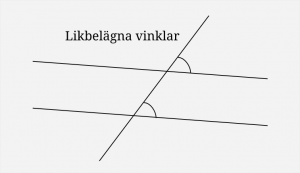
likbelagna

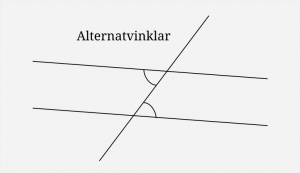
alternat

Jag gjorde genomgången av alla tre begreppen på en och samma bild och dessutom lite för hastigt, eftersom jag var ivrig med att komma igång med problemlösningen. Men i efterhand ser jag att det där med ”vedertagna fakta” inte uppfattades av de flesta eleverna. Vi hade tjänat på att gå igenom dessa typer av vinklar noggrannare, långsammare och inte på en och samma bild.

Jag berättade också hur man brukar markera lika vinklar i en figur. Det spelar inte så stor roll vad man väljer för beteckning, så länge alla likadana vinklar är markerade på samma sätt. Man kan markera lika vinklar med lika många bågar eller med lika många streck på bågen eller med ett hjärta om man så vill.

Geometriuppgifter

Eleverna fick lösa uppgifter om vinklar i kanske 35 minuter. De flesta försökte på egen hand, några samarbetade och var två och två. Efter varje uppgift har jag har skrivit upp några av typiska svårigheter och frågor som eleverna (och lärarna) hade, samt hur det gick för dem att lösa uppgiften.

1. Två linjer skär varandra. En av viklarna som bildas är lika med 41°. Vad är de andra tre vinklarna lika med?

Eleverna tolkade som att bilden ”vertikalvinklar” hörde till den uppgiften (eftersom den fanns direkt bredvid). Till elever, som hade svårigheter med frågan, gav jag ledtrådar av typen ”vilka vinklar är lika på bilden?”, ”vad vet man om summan av de alla fyra vinklarna?”. Efter det hade de flesta inga problem med att lösa uppgiften.

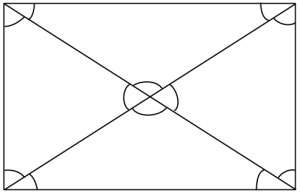
2. Markera så många lika vinklar som möjligt i a) en kvadrat c) ett parallellogram:

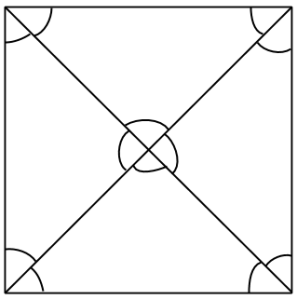
kvadrat_vinklar

b) en rektangel

rektangel_vinklar

c) ett parallellogram

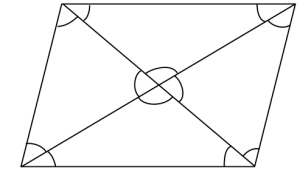
parallellogram_vinklar

Eleverna hade inga problem med att markera de parvis lika vinklarna (förutom en överanvändning av streck i vissa fall, en vinkel med fem överstrykningar gick inte att skilja från en vinkel med sex överstrykningar, och där gav jag rådet att använda en annan beteckning). Men nästan ingen kunde motivera varför de markerade vinklarna var lika. ”Eftersom de är lika stora”, fick jag höra några gånger. Det var helt nytt med motivering inom geometri för de flesta eleverna. Därför krävde vi inte någon rigorös förklaring på alla egenskaper hos figurerna, men stannade och diskuterade gärna om sätt att dra slutsatser på. Helt enkelt visade vi hur problemen kunde angripas strikt matematiskt.

Till exempel kunde vi fråga varför alla vinklar i mitten av kvadraten (där diagonalerna skär varandra) var lika stora och nöja oss med svaret ”kvadraten består av fyra likadana trianglar”. Men ingen refererade till ”likbelägna” eller ”alternatvinklar”, antagligen på grund av ovanan vid axiomatiskt resonerande (eller min hafsiga genomgång). Skönt i alla fall att eleverna höll med Euklides om att dessa axiom gäller :)

3. Vad är vinkelsumman i a) en triangel? b) en fyrhörning?

Här skrev de flesta eleverna ner rätt svar, men nästan ingen hade någon som helst motivering till det. På grund av detta stannade vi upp i den enskilda problemlösningen och hade en gemensam slutledning om varför vinkelsumman i en triangel alltid är 180° (ALLA visste det, men INGEN hade sett något bevis för det). Eleverna hittade på ett spännande sätt som gick ut på att kopiera triangeln och lägga den upp och ner ett par gånger. Vi behövde fortfarande använda ”alternatvinklar”-axiomet, men det sjönk nog ändå inte in att vi använde det. Det kommer ta ett tag innan gruppen är vana vid bevis!

Vad gäller förhyrningen så hade ett par elever bra idéer som gick ut på att en fyrhörning består av två trianglar (vilket ju egentligen räcker för att bygga ihop ett riktigt bevis). Vi gick igenom det på slutet av geometrimomentet och då tog jag även upp icke-konvexa fyrhörningar.

4. En linje skär två andra parallella linjer. Bestäm vinkeln mellan de mostående inre vinklarnas bisektriser.

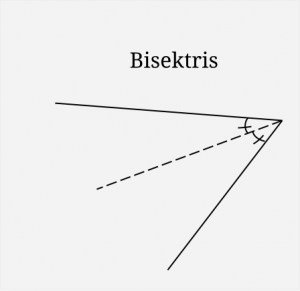
bisektris

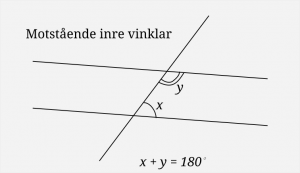
mostaende_inre

Eleverna som satte sig in i uppgiften kunde hitta lösningen genom att kombinera dessa två definitionsbilder. Jag kan tänka mig att om uppgiften skulle ha tagits upp på någon annan träff, så skulle en del inte kunnat lösa den. Men i samband med temat ”vinklar” och ett par ledande bilder blir den tvärtom ganska lätt.

5. Går det att rita fem strålar från en punkt så att det bildas exakt fyra spetsiga vinklar mellan strålarna? Vinklar mellan varje par av strålar räknas, inte bara mellan grannstrålarna.

Det behövdes några förtydliganden för vad som gäller i den här uppgiften, men de flesta hade en intuitiv känsla för vad strålar och spetsiga vinklar är för något. Under genomgången fick en elev komma fram och visa sitt exempel (som för övrigt inte är trivialt att konstruera). Totalt var det kanske 5 elever som hade löst uppgiften (och velat gå fram till tavlan).

6. Yttervinklarna för triangel ABC vid hörnen A och C är lika med 115° respektive 140°. En linje, som är parallell med AC, skär sidorna AB och AC i punkterna M och N. Bestäm vinklarna hos triangeln BMN.

En fråga som många av eleverna (och till med någon av lärarna!) inte visste svaret på, var vad ”yttervinkel” är för något. En av lärarna läser inte uppgifterna i förväg av pedagogiska skäl, det vill säga för att titta på uppgifterna med samma nya ögon som eleverna på lektionen. Men kanske är det inte en strategi som håller. Det var hur som helst det ordet eleverna fastnade på. Men ett par elever hann ändå klara uppgiften, med det var inte jag personligen som lyssnade igenom lösningarna.

Ladda ner för utskrift

Allt som allt var geometri och vinkeljakt ett svårt ämne, framförallt för att eleverna var så ovana. Fördelen är att alla då är på samma villkor, ingen hade mycket mer förkunskaper än någon annan. Jag hoppas att eleverna gillade att upptäcka nya saker om vinklar och bevisföring. Om någon inte gjorde det, så kan det bero att det var ett för stort kognitivt steg att direkt hoppa in i bevisens värld eller så gillade kanske inte personen att hålla på med helt nya saker (och kanske hellre ville syssla med något bekant). I det senare fallet tror jag inte Matteklubben är en rätt aktivitet för personen, då vi kommer att hålla på med nya tankesätt varje träff.

Som jag har nämnt ovan, att motivera sina lösningar från grunden (använda sig av axiom) var någonting som var helt nytt för eleverna. När man pluggar matte möter man ofta olika typer av bevis (till exempel beviset för Pythagoras sats), men man ombes inte alltid att konstruera bevis själv. Egentligen är en motiverad lösning till vilken uppgift som helst ett bevis i sig, men brukar inte kallas för det. Därför är många universitetsstudenterna rädda för att hitta på bevis, de förstår inte hur man går till väga.

Tanken är att eleverna på Matteklubben så småningom inte ska bli rädda för att motivera saker så utförligt som möjligt. Det handlar dels att lära sig om vad som är allmänt vedertaget fakta (t.ex. behöver man inte bevisa att 1 + 1 = 2, trots att det egentligen går att motivera), med också vad som inte är det. Och dels om att bli säker på att man inte missat några möjligheter i sitt bevis. Den känslan utvecklas när man blir bra på logik och kombinatorik, vilket vi ofta övar på när vi löser blandade uppgifter.

Jag har bloggat om bevis tidigare: Vad är ett fullständigt bevis?, Att bevisa. Ett exempel på ett bevis hittar du här: Klassiska bevis: roten ur 2 irrationellt.

HMT

I samband med att tävlingen HMT hålls den 11:e november ville jag lägga ner en del av lektionen på att informera om den och att träna inför den genom att lösa gamla problem. Bara några stycken i gruppen hade hört talas om Högstadiets Matematiktävling, vilket kanske inte är så konstigt, eftersom få skolor i Uppsala har deltagit de senaste åren. (En elev som var med på första träffen hade dock gått till final förra året och presterat bra!)

Eleverna som går i Matteklubben är de mest lämpade att delta, men för att de ska kunna göra det, behöver deras lärare vara delaktiga. Därför fick alla ett informationsblad som de kunde ge till sina respektive lärare. Sista anmälningen är den 4:e november och det går att läsa mer om tävlingen på HMT:s hemsida.

Jag hoppas att några elever vill delta, de har en god chans att ta sig vidare till final! Oftast behöver man lösa ungefär 4 problem (av 6) för att gå vidare. Men det är förstås frivilligt och man ska bara tävla om man tycker att det är kul.

Övning inför tävlingen

Vi hade bara någon halvtimme kvar av lektionen för att öva på gamla HMT-problem. Men klassen hann lösa alla uppgifter en minut innan lektionen skulle sluta! Det vill säga varje uppgift löstes av åtminstone en elev. Även om jag sade att uppgifterna inte var ordnade i svårighetsgrad, så försökte de flesta ändå att lösa uppgifterna i ordningen de stod, det är ju svårt att avgöra svårighetsgraden innan man har ett hum om uppgiften.

Utvärdering

Som det märks från mängden material som vi hinner ta upp under en lektion, så kan eleverna ta in en hel del kunskap. Men de har inte riktigt lärt sig att tillämpa allt vi pratar om. Det är inte så konstigt. Det är ganska lätt att visa häftiga saker för intresserade elever, kanske berätta om sitt eget sätt att se på matte eller visa en naturvetenskaplig grej som någon annan har kommit på (sådant som förekommer på tekniska museer). Men det är svårt att lära ut genomförande, det vill säga förmågan att komma på egna häftiga saker. Det tar många år av arbete och träning.

Det är dock väldigt viktigt att ta vara på intresserade elever, eftersom de i framtiden kommer att kunna bli riktigt bra ingenjörer eller forskare (eller något annat häftigt). Målet är ju att de ska komma på nya saker och därför behöver de att träna på den förmågan. Däri ligger Matteklubbens styrka och utmaning! Det finns hur mycket som helst i matematiken som bjuder in till upptäckter, men det gäller att välja sådan material som passar eleverna. De ska ha en chans att både göra upptäckter som någon annan har gjort före dem, men också ha möjligheter för att hitta på helt nya lösningar!

Första träffen med Matteklubben, åk 7-9

Matteklubben har haft lektioner för grupperna åk 2-4, åk 5-6 och sist ut var högstadieeleverna, åk 7-9.

Denna gång kom en hanterbar mängd elever, 25 stycken. Det är ganska lagom för den åldern, nackdelen med för många elever är att någon som är blyg inte törs föra fram sin talan. Jag tror att det kommer bli bättre med det när eleverna har lärt känna varandra lite. I framtiden kanske vi kommer blanda om dem och få dem att jobba lag, men under lektionerna jobbade de antingen själva eller grupper om 2-3, så som det föreföll naturligt för dem.
Vi var fem lärare och de flesta stunderna fanns det någon som inte var upptagen och som eleverna kunde fråga om det var något de undrade.

Blandade problem

Vi började med en timme med blandade kluringar (precis som i åk 5-6). Eleverna fick lösa dem i par och sedan berätta lösningar för oss när de var redo. Problemet var att nästan ingen räckte upp handen. Men när en lärare väl kom fram till en godtyckligt grupp elever så hade de nästan säkerligen löst en eller två stycken kluringar. Stor skillnad där mot yngre årskurser, kanske för att äldre barn redan har vant sig att de inte får uppmärksammad lärartid när de har presterat.

Kluringarna var inte helt självklara för alla, även om de flesta kunde klara av många av dem. Några var inte vana vid den typen av problem och då kunde man lätt missuppfatta villkoren. När vi kommunicerade med eleverna försökte vi fostra matematiskt tänkande hos dem med hjälp av följande frågor.

1. Går det att sätta in en av symbolerna +, -, *, / i varje mellanrum och sedan sätta ut
parenteser så att resultatet av uträkningen blir exakt 100?

2 2 2 2 2 2 2 2

Missuppfattningar/funderingar: Några förstod tvetydigheten som att man bara kunde använda sig av samma symbol (det vill säga välja en av symbolerna +, -, *, / och sedan bara sätta ut den). Någon glömde bort att man kan sätta ut parenteser. Vissa misstänkte att det inte gick att göra, men visste inte hur de skulle kunna förklara det.

Frågor/ledtrådar till eleverna: Försök att dela upp 100 i faktorer. Om du har fått en fyra, vad måste du få av resten av tvåorna (eleverna svarar korrekt att det är 25, men sedan måste man inse att det inte går med 25).

2. Piraterna A, B och C hade följande samtal.

A: ”B har 2 ögon.”

B: ”C har 2 ögon.”

C: ”A har 2 ögon.”

A: ”Vi tre har 2 ögon tillsammans.”

B: ”Vi tre har 3 ögon tillsammans.”

C: ”Vi tre har 4 ögon tillsammans.”

Det visade sig att var och en av piraterna ljög lika många gånger som han hade ögon. Hur många ögon hade var och en?

Missuppfattningar/funderingar: Eleverna förstod det som att ett svar räckte. Men för en fullständig lösning behövs att man redovisar alla svar eller förklarar varför fler svar, än de angivna, inte finns.

Frågor/ledtrådar till eleverna: När eleverna förklarade hur de tänkte, utgick de från antaganden, t.ex. ”Piraterna har 4 ögon tillsammans”, men sedan inte betraktade fallet då piraterna inte hade det. Då bad vi dem att gå igenom de missade fallen. Det var ganska omfattande och säkerligen missade vi några fall i diskussionen (det är inte helt lätt för läraren att följa), men eleverna fick en övning i logiskt resonerande och falluppdelning.

3. I ett tomt akvarium lade man ner några glaskulor och fyllde upp med vatten. När man sedan plockade ut hälften av kulorna, sänktes vattennivån i akvariet med en tredjedel. Hur mycket kommer vattennivån sjunka om man plockar ut hälften av de kvarvarande kulorna?

Missuppfattningar/funderingar: Många elever räknade ut andelen som vatten kommer sjunka i andra omgången relaterat till hur mycket vatten det fanns från början (d v s en sjättedel). Men det man undrar över är hur mycket vattnet kommer sjunka i förhållande till sitt dåvarande mängd. (Om man skulle säga ”Vattennivån sjönk med en sjättedel”, då skulle man mena något annat än det som händer i uppgiften.) När de räknade och jämförde bråk hade de oftast ”enheterna” i huvudet (det vill säga att 1/6 och 1/2 kunde beteckna andelar av helt olika saker), men då blev man lätt osäker vad ”enheten” för det slutgiltiga svaret blir.

Frågor/ledtrådar till eleverna: Räknar du med andelen av vattennivån i början eller efter första steget? Det man undrar över är det senare, det vill säga, hur stor andel av vatten i mitten av handlingen försvinner?
Om det är svårt att hålla reda på mängderna så kan du rita en bild.

4. En man har ett litet hål i väggen (lika stor som en punkt). Han har också ett märke som han kan hänga upp (se bilden). Markera alla punkter, där han kan sätta spiken, så att hålet täcks av märket.

spik

Missuppfattningar/funderingar: Var ligger hålet? Hur stort är det? Här behövdes förklaringen att hålet är lika stort som en punkt och att svaret frågas i förhållande till det utsatta hålet.

Frågor/ledtrådar till eleverna: Markera en punkt. Skulle vi kunna sätta spiken där (markerar en punkt ett steg uppåt från hålet), kommer flaggan täcka hålet då? Vi frågar om några positioner till och eleverna svarar antingen ”ja” eller ”nej”. Vi förklarar att det som frågas efter är helt enkelt figuren som bildas av punkter där man kan sätta spiken. (Eleverna kommer då oftast fram till rätt svar själva.)

Ladda ner för utskrift

Genomgång av blandade problem

Vi lade ner åtminstone 15 minuter på att gå igenom de blandade problemen ordentligt. Eleverna fick presentera olika lösningar på tavlan. Längst tid tog uppgifterna 2 och 3.

På uppgiften om piraterna kom vi tillsammans fram till en uttömmande lösning. Eleverna kom med bra idéer om att utesluta vissa fall av total mängd ögon (t.ex. att piraterna måste ha ljugit minst två gånger på grund av de sista tre utsagorna). De såg också symmetrin i de första tre utsagorna, vilket gjorde att vi inte behövde betrakta tre olika fall hela tiden utan kunde sammanfatta dem (en av de första tre utsagorna är falsk, två av de första tre utsagorna är falska, etc.)

Uppgiften om akvariet var det många som ville förklara hur de tänkte på. Det var bra att öva för eleverna att redovisa inför grupp, eftersom då anstränger man sig extra för att förklara korrekt och tydligt (vilket är en av sakerna man kommer lära sig av att gå på Matteklubbens träffar). Många höll med om att rita en bild på akvariet underlättade lösningen. Några av eleverna satte i konkreta värden (höjd eller volym på akvariet) för att räkna ut svaret, men vi lade inte så mycket vikt vid huruvida det var rätt eller fel att göra. Däremot konstaterade vi (kanske något otydligt just då) att det blir på samma sätt oavsett vilka värden man antar. Det hela handlar om att gå från konkreta och bekanta enheter (cm eller l) till skummare enheter (andelar av totala volymen), vilket är ett svårt steg att ta om man går i sjuan t.ex. Vi kommer att så småningom vänja eleverna vid det generella tanksättet (om de inte redan är vana vid det).

Eftersom det inte fanns så mycket kvar tid till andra halvan av lektionen, ritade vi bara upp svaret på uppgiften om flaggan, men förklarade inte särskilt noga varför det var just svaret. Ska man vara matematiskt petig borde vi ha gjort det, det vill säga visat exakt varför punkterna innanför figuren fungerar som spikplatser och punkterna utanför figuren inte gör det. Däremot förstod eleverna det rätta svaret på ett intuitivt sätt (efter att ha experimenterat).

Delbarhetsprinciper

Dagens tema var delbarhetsprinciper, det vill säga principer och regler för hur man snabbt kan se om ett tal är delbart med något givet annat tal eller inte. Det klassiska exemplet är att man kan se att ett tal är delbart med 2 (d v s jämnt) om den sista siffran är 0, 2, 4, 6 eller 8 (d v s sista siffran är jämn). Detta skrev jag upp som

$\text{Sista siffran } \vdots 2 \Rightarrow \text{ talet } \vdots 2$

Jag använde symbolen $\vdots$ som ”delbart med” för att det är praktiskt. Man kan också använda $|$ i betydelsen ”delar” (t.ex. 5 delar 10), men i fallet ovan var det språkligt opraktiskt.

Eleverna kände till fler delbarhetsprinciper och vi skrev upp dem för 5, 3 (och 9) och 4:

$\text{Sista siffran } \vdots 5 \Rightarrow \text{ talet } \vdots 5$

$\text{Siffersumman f\$

$\text{Talet som bildas av de tv\aa{} sista siffrorna } \vdots 4 \Rightarrow \text{ talet } \vdots 4$

Egentligen gäller påståendet åt andra håller också, och det använde vi under lektionen. Men för att inte förvirra eleverna för mycket med ny notation, använde jag implikationspil (som man ändå fattar som ”pil”) istället för en ekvivalenspil (dubbelpil).

Vi förklarade tillsammans varför delbarhetsprincipen med 4 gäller. Vi delade upp ett konkret stort tal i hundratal och det som blir över (talet som bildas av de två sista siffrorna). Sedan insåg vi att 100 ligger i fyrans tabell och därmed hänger det bara på det sista talet, huruvida det stora talet är delbart med 4. Eleverna förstod beviset.

Många hade tydligen hört några av delbarhetsprinciperna förut, men de flesta kunde inte förklara varför de gällde. De som inte hade bevisat det förut hade även svårare för att komma ihåg dem också under problemlösningsdelen. Så jag tror att det var väldigt nytt och nyttigt med bevis.

Kluringar om delbarhet

Eleverna fick lösa följande kluringar på temat delbarhetsprinciper. Ofta utnyttjade de inte principerna utan kom fram till svar på annat sätt. Men de fick ledtrådar när de hade kört fast och då förstod de hur delbarhetsprinciperna kunde komma till nytta. Följande dialoger kunde ske under diskussionen av respektive uppgift.

1. Skriv en siffra till vänster och en siffra till höger om 10 så att det nya talet blir delbart med 12 (det vill säga blir ett tal där divisionen med 12 går jämnt upp).

Elever: Vi kommer inte fram till något svar.
Lärare: Tänkt på att talet är med 12:ans tabell. Vilka andra tabeller måste talet vara med i?
Elever: Fyrans, sexans, treans…
Lärare: Var vet om tal som är med i fyrans tabell?
Elever citerar delbarhetsprincipen med 4.
Lärare: Och vad vet om tal som är med i treans tabell? Skulle vi kunna kombinera det vi vet för att hitta ett svar?
Elever: Ahaa, smart.

2. Skriv 2014 efter sig själv några gånger så att talet som bildas blir delbart med 9.

Elever: Vi skrev upp 2014 efter varandra och dividerade (vi kunde fortsätta divisionen genom att skriva till några fler 2014) tills det gick jämnt ut.
Lärare: Är det en slump att det blev just 9 stycken?

Elever: Vi skrev upp 2014 efter varandra så att siffersumman blev delbart med 9.
Lärare: Är det en slump att det blev just 9 stycken?
Elever: Nej, siffersumman blir ju 9 gånger siffersumman av 2014.

3. Kan ett tal som bara består av fyror vara delbart med ett tal som bara består av treor? Och tvärtom?

Elever: Vi tror att svaret är ”nej”.
Lärare: Varför det?
Eleverna börjar resonera och kommer fram till att svaret är ”ja” på den första frågan.
Lärare: Och på andra frågan?
Elever: Kanske är svaret ”ja” här också…

4. I rutorna på en 5×5 står siffror som inte är lika med 0. Av alla raderna och kolonnerna bildas 10 femsiffriga tal. Kan det hända att alla tal utom ett är delbara med 3?

Elever: Kollar man på alla talen?
Lärare: Nej, de som bildas av de 10 raderna (vågräta och lodräta).

Elever: Ja, man kan ha siffror som är delbara med 3 och ändra en av dem.
Lärare: Men då ändrar man två av talen, inte ett.
Elever: Justja…

5. Ett kvadrattal slutar med siffran 6. Visa att den näst sista siffran är udda.

6. Från ett tal subtraherade man talet skrivet baklänges. Visa att resultatet måste vara delbart med 9.

De sista frågorna hann vi knappt, eftersom tiden höll på att ta slut.

Ladda ner för utskrift

Bevis för delbarhetsprincipen med 3

Som exempel tog vi ett större tal och framme på tavlan kom tillsammans fram till att man får siffersumman av talet genom att dra bort tal som är delbara med 3 (för varje tiotal, hundratal, tusental etc. drar man bort ett visst antal 9:or, 99:or, 999:or etc.). Det blev lite oorganiserat på tavlan, så jag vet inte om majoriteten hann förstå beviset. Möjligen borde vi ha gått igenom beviset för talet 9, vilket i stort sett sammanfaller med bevist för 3, men kanske är något självklarare.

Det var kul att träffa intressanta och intresserade högstadieelever! Till vi ses nästa gång, fundera på och diskutera gärna hemmakluringen.

HMT-kval 2013

För circa en månad sedan hölls kvalomgången i Högstadiets Matematiktävling. Det är en tävling i problemlösning som riktar sig till årskurs 6-9, men självfallet lyckas eleverna i årskurs 8-9 få bäst resultat. Därför är det mest elever från dessa årskurser som går vidare till finalomgången.

Därmed inte sagt att de inte kan gå bra för elever i åk 6-7! Det de eventuellt saknar är några kunskaper om geometri samt delbarhet, vilket ett par av årets kvaluppgifter gick ut på. Däremot kunde man klara sig riktigt bra även om man ”bara” hade löst fyra uppgifter av sex. 10 poäng räckte nämligen för att gå till final (3 poäng tilldelas för varje korrekt löst uppgift). Du kan läsa mer om årets omgång på HMT:s hemsida, medan vi tittar närmare på själva uppgifterna.

Problem 1

Det går att skriva tal i rutorna i ﬁgur 1 så att om man följer pilen från en ruta och
använder räkneoperationen som står vid pilen så får man talet i nästa ruta.

Vilket tal är då X? Ange även en möjlig räkneoperation att ersätta frågetecknet med.

Lösning

Strategin är att gå baklänges från 13 till X på vägen gjord av pilarna till vänster. Till 13 kommer vi genom att dela med 2, så talet innan måste vara 26. Till 26 kommer vi genom att subtrahera 1, så talet innan är 27. Innan dess multiplicerade vi talet med 3, så talet innan måste ha varit 9. Och från X kom vi till 9 genom att subtrahera 11, så X måste ha varit 20.

På samma sätt kan vi bestämma talen på högra pilvägen. Till 13 måste vi ha kommit från 18, till 18 från 12, till 12 från 6. Om vi ska komma från 20 till 6 så kan operationen under frågetecknet vara -14 till exempel.

Kommetarer

Det här en typiskt uppgift nästan alla tävlande klarar av. Man hoppas ju innerligt att ALLA elever i åk 9 ska kunna klara av en sådan uppgift. Men så är tyvärr inte fallet, vilket bara beror på att dessa elever antagligen skulle missförstå uppgiften.

En grej man inte tänker på när man är van vid ekvationer är att ”x2” och ”x3” skulle kunna misstolkas att handla om ”X”. Bokstaven ”X” står i mitten för att göra uppgiftsformuleringen tydligare, men kan tvärtom skrämma elever som inte gillar ekvationer. Man skulle kunna ställa upp lösningen på första halvan av uppgiften såhär:

((X – 11)*3 – 1)/2 = 13

Men hur kul formulering är det? Vilken av formuleringarna uppmanar till någorlunda kreativt tänkande och vilken till att ”komma ihåg och tillämpa inlärd metod”? Just det, olika formuleringar på samma uppgift blir pedagogiskt sett helt olika uppgifter! De flesta elever tror jag skulle lyckas lättare på den första formuleringen. Något att tänka på när man introducerar ekvationer i skolan.

Problem 2

Om talet A vet vi följande:
- Talet A ger resten 5 när det delas med 11.
- Talet A ger resten 4 när det delas med 9.
- Talet A ger resten 5 när det delas med 7.
- Talet A ger resten 4 när det delas med 5.
Vilken rest får man när man delar A med 3?

Lösning

Svaret kan vara antingen 0, 1 eller 2, eftersom inga andra rester förekommer när man dividerar med 3. Talet A kan vara hur stort som helst, men vi försöker ”få plats” med så många 3:or i talet som det bara går.

För det kan vi använda att talet A har rest 4 när det delas med 9. Det betyder att man får plats med ett antal 9:or och det blir 4 över. Men en 9:a är ju tre 3:or, därför vet vi att talet A innehåller ett ännu större antal 3:or, men det viktigaste är att det blir 4 över. Där får det plats en 3:a till och det blir 1 över. Därför är resten lika med 1.

Kommetarer

Svårigheterna med att lösa den här uppgiften består av att man inte vet vad division med rest innebär, eftersom man inte fokuserar så mycket på just rester i skolan. Och även om man vet vad resten är, så kanske man försöker bestämma talet A, vilket inte ger ett heltäckande resultat (det finns flera tal A som har de nämnda egenskaper, till och med oändligt många sådana tal finns det). Och så är det förstås vilseledande att det bara villkor två som är viktigt.

Tar man sig igenom de hindren, så är inte uppgiften svår.

Problem 3

På Skänkvägen står elva hus på rad, numrerade från 1 till 11. Eftersom sämjan bland
grannarna är god, så bjuds det ofta på middag. När man bjuder på middag bjuder man
in de två närmaste grannhusen på båda sidor. Om man inte har två grannar på någon
sida bjuder man alltså in färre grannar, till exempel bjuder hus 2 in grannarna i hus 1, 3
och 4.

En dag ärver familjen i hus 2 en riktigt, riktigt ful tavla. När familjen nästa gång blir
bjuden på middag bestämmer man sig därför att ge bort tavlan till kvällens värd. Men
tavlan är så ful att ingen på gatan vill behålla den, så vid första möjlighet ger man därför
bort den till den middagens värd. Av artighetsskäl kan man såklart inte ge tillbaka tavlan
till någon man själv fått den av, och inte heller till någon man själv redan en gång givit
bort den till.

Vem kommer till slut att vara tvungen att behålla tavlan?

Lösning

Vi hoppar vilt i svårighetsnivån! Vi ”finkammar” uppgiften lite först, för att senare lättare kunna formulera lösningen.

Man kan bara ge bort/ta emot tavlan av hus som ligger 1 eller 2 steg bort ifrån ens eget. Om hus A gav bort tavlan till hus B så är den förbindelsen A-B ”förbrukad” eftersom tavlan inte får ges på samma sätt och inte heller ges tillbaka från hus B till hus A. Således kan vi rita ut alla förbindelser och tänka oss att tavlan vandrar längs med dem och ”förbrukar” dem (husen ligger på rad, men att vi ritar dem på en cirkel spelar ingen roll, det är förbindelseschemat som är det viktiga):

tavlan

Låt oss för en stund strunta i var tavlan börjar sin väg (hus 2). Vi tänker istället på var tavlan kan sluta (någon annanstans i hus 2?). Kanske slutar tavlan i hus 4, så vi tittar på förbindelser som har med hus 4 att göra:

tavlan_hus

Om hus 4 är huset som inte kan skicka tavlan vidare, så betyder det att tavlan kom till dem och i och med det var alla förbindelser förbrukade. Hur förbrukades förbindelserna? Varje gång hus 4 fick tavlan så förbrukades nästa förbindelse genom att de gav bort den, och tvärtom. Så eftersom tavlan inte började där, måste förbindelserna förbrukats i ordningen: fick – gav bort – fick – gav bort. Därför kunde inte hus 4 fått tavlan på sin sista förbindelse.

Husen 3, 5, 6, 7, 8, och 9 befinner sig i samma situation. De har fyra förbindelser var och därför följer samma schema, om nu alla fyra förbindelserna skulle förbrukas: fick – gav bort – fick – gav bort.

Samma sak är det egentligen för husen 1 och 11 som har två förbindelser var. Får de tavlan, så har de ju möjlighet att ge bort den.

Därmed är det bara hus 2 och 10 kvar. Hus 2 har tavlan från början och därför följer schemat ”gav bort – fick – gav bort”, OM vi är säkra på att alla förbindelser förbrukas. Därför är hus 10 det enda huset som kan ha kvar tavlan utan att kunna ge bort den.

En möjlig väg för tavlan kan vara 2 -> 4 -> 6 -> 8 -> 10 -> 11 -> 9 -> 10. Nu kan hus 10 inte ge bort tavlan.

Kommetarer

Läsaren som är bekant med grafteori förstår att så fort vi har ”kammat” problemet så handlar det om i princip Eulerstigar. Men enkel formulering kan man säga att en figur, som man ritar utan att lyfta pennan från pappret, har som mest två punkter, varifrån det utgår ett udda antal linjer. En av punkterna kommer då vara startpunkten och den andra slutpunkten.

Problem 4

I parallelltrapetset ABCD är sidan AB 50% längre än sidan CD. Punkten P
är diagonalernas skärningspunkt. Arean av triangeln ADP är 12. Bestäm arean av hela
parallelltrapetset.

Lösning

Parallelltraps är en figur med två parallella sidor (det syns på bilden att det är AB och CD som är parallella). Om man ritar ut diagonalerna bildas det flera alternatvinklar, varav två par är inbördes lika. Det följer då att trianglarna APB och CPD är likformiga.

alternatvinklar

Vi färgkodar de fyra små trianglarna som syns på bilden:

parallelltrapets_slutsatser

Vi kom fram till att brun och röd var likformiga. De är dessutom likformiga med koefficienten 1,5 (eftersom röds motsvarande sida var 50% länge än bruns).

Vi vet även att blå+brun har samma area som grön+brun, eftersom båda dessa stora trianglar har samma bas DC och lika lång höjd (avståndet mellan de parallella linjerna). Därför har blå och grön samma area och vi vet från uppgiften att det är 12.

Blå och röd har samma höjd om vi tar DP pch PB som baser. Med DP och PB är motsvarande sidor hos den bruna och den röda triangeln. PB är alltså 1,5 gång större och då han även röd 1,5 gånger större area än blå, 12*1,5 = 18.

Blå och brun delar höjd om man nu väljer AP och PC som baser. Även här är PC 1,5 gånger mindre än AP. Så arean för brun är även den 1,5 mindre än arean för blå, det vill säga 12/1,5 = 8.

Därmed har vi bestämt alla de små trianglarnas areor. Arean för hela parallelltrapetser är
röd + brun + grön + blå = 18 + 8 + 12 + 12 = 50 (areaenheter)

Kommetarer

Måste erkänna att jag försökte lösa den här uppgift snabbt och misslyckades! Hade en alldeles för avancerad lösning och räknade fel någonstans på vägen. Så här ska man kunna ”lagom” mycket geometri :)

”Lagom” mycket geometri innebär bland annat: parallellitet, alternatvinklar, vertikalvinklar, likformiga trianglar, likformighetskoefficient, arean för en triangel, val av bas/höjd i en triangel. Inte så lite man ska kunna!

Framför allt ska man vara skolad för att genomföra bevis för att redovisa uppgiften på ett korrekt sätt. Geometriundervisningen som bygger på axiom/bevisföring har i princip försvunnit från svenska skolor, därför lyckades nästan ingen av deltagarna lösa (eller ens få poäng) på den här uppgiften. Jag tvivlar på att särskilt många gymnasister skulle kunna lösa den här uppgiften heller.

Problem 5

Genom att ﬂytta om siffrorna i talet 2013 kan man få 18 olika fyrsiﬀriga tal. På hur många
sätt kan man välja två olika av dessa 18 tal så att deras summa är precis lika med ett av
de återstående 16 talen?

Lösning

Provar man lite så ser man att det här aldrig går. Hur förklarar vi det här på ett allmängiltigt sätt?

Om två tal som bara består av siffrorna 0, 1, 2 och 3 adderas, så kommer entalen, tiotalen, hundratalen samt tusentalen adderas var för sig, eftersom siffrorna är så pass små. Men det betyder att siffersumman för resultatet av additionen kommer vara lika med siffersumman för det första talen adderat med siffersumman för det andra talet.

Detta kan ju inte hända, eftersom siffersummorna för alla talen är 6. Därför kommer siffersumman för resultatet att bli 12 och det kan inget av talen i uppgiften ha.

Kommetarer

Den här uppgiften kan lösas på mängder av olika sätt, jag angav det kortaste jag kunde komma på. Sätter eleven in sig i uppgiftens formulering, så är resultatet mer eller mindre uppenbart. Hur man ska förklara resultatet är däremot inte lika uppenbart.

Jag tror att många elever känner intuitivt att det har med siffersumman att göra, men de är inte vana vid att formulera lösningar på det sätt, med bevarande av siffersumma och dylika termer. Därför gissar på att de använde mer krångliga förklaringar. Det kan vara frustrerande att försöka förklara något som är så pass uppenbart, men en bra övning om man vill bli bättre på att förstå och formulera egna bevis.

Problem 6

Rutnätet i ﬁguren skall fyllas med tal. I varje ruta (utom i understa raden) står summan
av de två talen i rutorna direkt under den. Vilket tal skall stå i den översta rutan?

Lösning

Den här uppgiften kan både lösas baklänges (nerifrån och upp) och framlänges (uppifrån och ner). Istället för att bara införa två variabler inför vi jättemånga, det vill säga betecknar varje okänt tal med en bokstav.
talpyramid_variabler

Talet A består av talen B och C.

Talen B och C består av talen D och 503 och 503 och E.

Talen D och 1006 och E består av talen 253 och F och 1006 och G och 251. Totalt alltså 1510 och F och G.

Inte har vi kommit fram till svaret än, men vet att pyramidegenskapen även gäller talet 503: att det består av talen F och G.

Så vi vet att talet A består av 1510 och F och G, med andra ord av 1510 och 503, det vill säga lika med 2013. Klart!

Kommetarer

Även här tror man kanske att hela pyramiden måste bestämmas för att avgöra det översta talet, men så är inte fallet. Det finns flera olika pyramider som ser ut på det sättet och alla måste då ha 2013 i toppen. Notera att det är på samma sätt som i uppgift 2 och uppgift 4 – flera olika konstruktioner uppfyller uppgiftsvillkoren, men ger ändå ett och samma svar i slutändan.

Ibland (eller kanske alltid) går matematik ut på att dra korrekta och allmängiltiga slutsatser i situationer där vi inte har tillgång till fullständig information.

Pizzasats nummer 1

Geometri är inte bara någonting skäggiga greker höll på med, utan den kan vara användbar även för den gemene svensken – till exempel när man ska dela en rund pizza!

Om man får en pizza hemkörd och ska dela den på två personer, så brukar man skära pizzan i två halvor. Problemet är att om man inte skär precis genom mitten, så kommer inte halvorna att bli lika stora.

En metod som garanterar rättvis fördelning av pizzan är följande. Välj en punkt inuti pizzan, vilken som helst, och gör fyra snitt, med $45^\circ$ graders vinkel emellan.

Då, om ena personen får varannan utav bitarna som bildas, medan den andra får resten, så kommer båda få exakt hälften utav pizzan.

Den generaliserade versionen av pizzasatsen, där man kan dela pizzan i ännu fler delar med lika stor vinkel mellan snitten (12, 16 delar osv.), bevisades av L.J.Upton 1968.

Man kan bevisa satsen på olika sätt, men bland annat finns ett bevis som består av en enda bild.

Nyfiken på beviset? Se ledtrådarna nedan i så fall.

Visa ledtråd 1

Visa ledtråd 2

Vad är ett fullständigt bevis?

När man löser ett riktigt matematiskt problem räcker det inte att presentera svaret. Du måste presentera lösningen också, det vill säga hur du kom fram till svaret. Ibland har inte problemet något svar, utan du skall bevisa att något påstående är sant. Hur vet man att beviset är fullständigt? Ett sätt är att berätta beviset för en kompis. Om du övertygar denne om att du har bevisat det du skulle, så är ditt resonemang antagligen korrekt. Ett annat sätt är att själv försäkra sig om att man inte glömt att undersöka några möjligheter.

På vår mattecirkel får vi träna båda sätten! På en vanlig träff får man berätta lösningen för läraren och sedan få eventuella förtydligande frågor. På den första matteträffen denna termin körde vi dessutom tävlingen där deltagarna fick berätta lösningar för varandra. Denna tävling kallas mattedrabbning och man lär sig otroligt mycket på att både försöka övertyga motståndaren om att man har löst problemet rätt och, när man spelar opponentens roll, försöka fälla motståndaren med kluriga frågor.

Ta en titt på vår första lektion under fliken Cirkel.

Har du någon att diskutera problemen med, försöka att uttnyttja det. Du och den personen kommer lära er mycket om att resonera. Om du vill ha fler att prata matte med, och går eller tänker gå på Katedralskolan i Uppsala, välkommen på vår cirkel!

Klassiska bevis: roten ur 2 irrationellt

Flera av mina bekanta har berättat för mig vad deras första möte med riktiga matematiska bevis var. Och man märker kanske inte först att det man läser eller hör om är så kallade riktiga bevis, förrän man läser ordet ”bevis” explicit. De första sådana för var och en kunde ha varit bevis för Pythagoras sats, något induktionsbevis eller motsägelsebevis.

Här tänkte jag berätta om den mest klassiska klassikern av motsägelsebevis, nämligen att roten ur 2 är ett irrationellt tal.

Vad betyder irrationellt?

Ett irrationellt tal är ett tal som inte går att få med hjälp av naturliga tal 0, 1, 2, 3 …. och de aritmetiska operationerna +, -, * och /. Talen som däremot går att få på det sättet kallas rationella, till exempel $\frac{(5-10)}{3}=\frac{-5}{3}$ . Rationella tal kan alltså skrivas som bråk.

Irrationell och rationell är helt enkelt motsatser. På grund av den här negativa definitionen (det vill säga definiera något genom att använda ett ”inte”), är det naturligt med ett negativt bevis till påståendet (det vill säga motsägelsebevis).

Påstående: $\sqrt2$ är ett irrationellt tal.

Tankegång: Vi skall alltså bevisa att $\sqrt2$ inte är ett rationellt tal. Kan verka svårt först, vi kan ju inte riktigt testa alla möjligheter, alla bråk som överhuvudtaget går att få fram. T.ex. (bara ett exempel nu, helt onödigt för beviset!!!):

Är $\sqrt2=\frac{3}{2}?$ Nej, för då skulle deras kvadrater vara lika $2=\frac{9}{4}$ , vilket absolut inte är sant!

Men det finns oändligt många bråk, vi kan sitta och gissa bråk som är ungefär lika med roten ur 2 och sedan verifiera att de inte är exakt lika. Men bara för att vi inte kan hitta något bevisar inte att det inte finns!

Det är nu vi inser att det faktiskt skulle vara lättare att på något sätt testa alla möjligheter samtidigt. Med det menar jag att vi antar att det finns ett sådant bråk och vi sedan kommer fram till att det aldrig kan bli likhet med roten ur 2. Det är kärnan i alla så kallade motsägelsebevis: antag att det går (antag det positiva påståendet, det utan ”inte”) och kom fram till motsägelse.

Bevis: Antag att roten ur 2 är lika med något bråk. Förkorta bråket så långt det går, så att nämnaren och täljaren inte längre går att dela med samma heltal. Vi har alltså nu:

$\sqrt2=\frac{a}{b}$ och a och b är heltal som inte har någon gemensam delare.

Som förut försöker vi kontrollera likheten genom att kvadrera:

$2=\frac{a^2}{b^2}$ ,

så

$2{b^2}=a^2$ .

Varför är denna likhet omöjligt då? Vi tar hjälp av talteori, läran om heltal och delbarheter.

Vänsterledet $2b^2$ är ett jämnt tal, så högerledet, $a^2$ måste vara det också. Alltså går $a$ att dela med 2, dvs $a=2k$ , där $k$ är ett heltal. Skriv om likheten:

$2{b^2}=(2k)^2=4k^2$ .

MEN detta innebär ju att $b^2=2k^2$ så med samma resonemang som förut får vi att $b$ är ett jämnt tal. Men nu kommer vi fram till motsägelse, eftersom i situtationen då både $a$ och $b$ är jämna går det faktiskt att förkorta bråket (med 2). Nu är vi faktiskt klara.

Vi blev klara så fort vi fick motsägelse i vår lösning. Det är därför det heter motsägelsebevis.

Kan man lära ut matte med hjälp av spel?

Eller en ekvivalent fråga: kan man lära sig matte med hjälp av spel?

Jag har lagt till en spelsida på bloggen med lite snodda småpussel. Syftet med detta är ännu oklart, men det fick mig att tänka på ovanstående frågor. Så nu menar jag alltså spel för en person, säg datorspel.

Kännetecken för spel är det interaktiva, det som just är kärnan i allt lärande.

Säg till exempel att ni skall förstå situationen ”kontinuerlig, men inte deriverbar (i en viss punkt)”. Någon säger till er att denna situation förekommer och ni försöker förstå varför detta är möjligt. Ni kommer kanske på själva eller oftast berättar läraren rakt av exemplet y=|x|, beloppfunktionen. Aha, nu är det klart hur det kan vara möjligt!

spel

Något senare träffar ni på ett annat exempel, som den till höger. Och visst passar den och ni kanske kommer ihåg den i kort tid. Men om någon frågar er om en funktion som är kontinuerlig men inte differentierbar i alla punkter, så föreställer ni er först av allt y=|x|. Lite för att ni såg den först, men mest för att ni förstod den först.

Det kanske inte var ett jättebra exempel. Men fråga nästan vem som helst som har bevisat något. Om man bevisar någonting själv, men sedan får se ett snyggare och kortare bevis för samma sak, minns man ändå med all säkerhet sitt egna bevis, men inte det andra.

Därför är det helt avgörande för inlärningen hur mycket eleven själv får jobba.

Kan man då på något sätt få in matematikens lärdomar i ett spel? Vad är det man redan kan lära sig i existerande spel?

Tag sudoku till exempel. Brukar stå i tidningar ”träna din hjärna mha en sudoku varje dag” osv osv. Det sudoku egentligen tränar är:

1. Förmågan att se över mönstret och urskilja det viktiga, till exempel titta på alla 9:or och fylla i dem som saknas.

2. Tekniken ”systematisk fallundersökning”. Ifall det finns flera möjligheter för en viss siffra, så kanske man skriver en möjlighet lite smått i en ruta och försöker forsätta. Det viktiga här är att inte glömma alla fall.

3. Problemlösningförmågan ifall man löser svåra sudokun. Om man inte fuskar och läser på nätet så kanske man upptäcker en ny metod själv.

Det är inte mer än så. Det händer ännu mindre om man spelat på samma nivå länge.

Poängen med de spelen jag överhuvudtaget kan komma på är att de tränar ”skills” och inte lär ut någon kunskap/fakta. Mycket lättare är det för ämnet historia, många har lärt sig största delen spelandes Civilization och Europa Universalis och inte i skolan. Historia handlar per definition om människans interaktion.

Matematiken och andra naturvetenskaper är mycket mindre beroende av människan.

Ett bra mattespel skulle gå ut på att spelaren löser problem eller hittar bevis. Det får mig att tänka på spelen som liknar Myst, det vill säga quest-spel. Man spelar väsentligen genom att klicka på saker i rätt ordning, gå till olika platser och hitta samband mellan saker som händer. Brukar vara jättekul att spela tills man fastnar på någon svår sekvens.

Går det att göra något liknande med ren matematik? Säg att man samlar ihop lappar med definitioner och påståenden. Lägger man dem i rätt ordning, så kommer kanske ett lemma ut. Och sista bossen är Fermats stora sats!

Låter inte som världens mest spännande spel, men tål att funderas vidare på. Slutsatsen jag drar är att spel kan träna och utveckla specifika förmågor, som är nyttiga i matematikstudier. Logisk resonering, mönsterseende, allt detta kommer till nytta. Men förståelsen för matematisk teori verkar omöjlig att lära ut på något sätt som inte är ekvivalent med traditionell lärare eller bok.

Att bevisa

Idag startar min nya mattecirkel. Det är förvisso bara en elev i den än så länge, men jag kallar det hela mattecirkel i alla fall av en gammal vana. Mina mattecirklar brukar innehålla sådana problem som inte förekommer i vanliga skolan, utan snarare i matematiktävlingar, som HMT.

Det är svårt men ganska spännande att introducera någon till matematikvärlden. Vilka områden skall man lära sig mer om först av allt? Vilka problemlösningstekniker?

Det mest essentiella i matematikstudier är att kunna avgöra vad som är ett bevis eller inte. Sedan så småningom får man intuition för vad som är tillräckliga bevis eller inte. Till exempel blir studenter ganska ofta osäkra på ifall de kan anta ett visst påstående i kursboken eller om man ska visa påståendet. Eller hur många Gausseliminationer måste man redovisa för att uppgiften inte ska få avdrag?

Allt detta beror på i princip på erfarenhet, och man lär sig att avgöra sådana frågor efter några månader eller något år.

Hur började du med matematiken? Vilka bevis förstod du först av allt?

(Passande förresten att starta en mattecirkel på pi-dagen :) Grattis alla!)

Hemfrågan

Vinklar

Geometriuppgifter

Bevis

HMT

Övning inför tävlingen

Utvärdering

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Blandade problem

Genomgång av blandade problem

Delbarhetsprinciper

Kluringar om delbarhet

Bevis för delbarhetsprincipen med 3

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Problem 1

Lösning

Kommetarer

Problem 2

Lösning

Kommetarer

Problem 3

Lösning

Kommetarer

Problem 4

Lösning

Kommetarer

Problem 5

Lösning

Kommetarer

Problem 6

Lösning

Kommetarer

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?