Två pjäser på en 12-hörning
En svart och en vit pjäs står i två intilliggande hörn av en 12-hörning. På ett drag får man flytta en valfri pjäs till ett ledigt grannhörn. Man får inte gör drag som leder till att pjäserna står på ett sätt som de stått på förut. Hur många drag kan man som mest göra?
Jämn siffra efter udda
Jämn siffra efter udda
Vanda skrev talen från och med 1000 till och med 2000 i ordning på en rad som ett enda långt tal:
1000100110021003….19992000
Hur många gånger skrev hon en jämn siffra direkt efter en udda siffra?
(Jämna siffror är 0, 2, 4, 6, 8; udda siffror är 1, 3, 5, 7, 9).
Matematik i Genikampen – tredje avsnittet
Tredje avsnittet av Genikampen innehöll mycket matte! Så mycket att det inte hanns med att skriva om det innan avsnitt fyra kom ut. Avsnitt fyra och fem kommer jag däremot att slå ihop till ett inlägg.
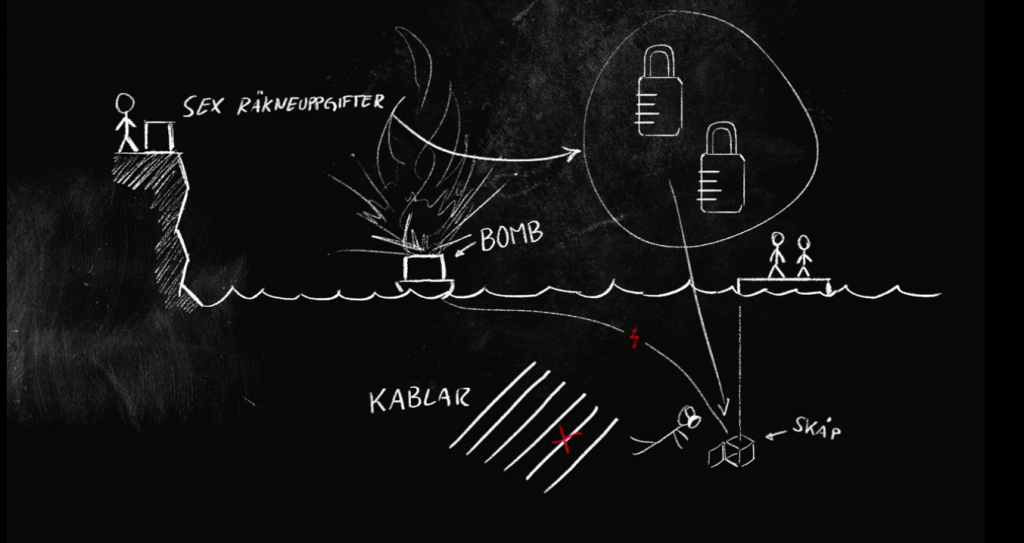
Avsnitt tre innehöll tre tävlingar: allmänbildningspyramiden, bombdesarmering och pussel i duellen.
Pyramiden
I pyramidtävlingen skulle vi välja ett av fyra svarsalternativ på varje fråga, ställa in lådorna med de sidorna framåt och sedan klättra upp på pyramiden för att få en kontroll. Programledaren Micke skulle då säga hur många rätt vi hade (men förstås inte vilka som var rätt) och då kunde vi ändra lådorna till nästa kontroll. Det gällde att få alla rätt, men hur ska man göra om man inte kan svaret på frågorna?
Hade man fått veta vilka frågor man hade fått fel på, så skulle det inte ta mer än fyra testomgångar för att lyckas få alla rätt — då tar man ju bara hela tiden nästa alternativ på de som är fel. Eftersom man bara får veta antalet, så gäller det att chansa lite vilka frågor man hade fått fel på.
Mer om detta senare, men i verkliga förloppet hade vi verkligen tur med att snabbt få noll rätt.

Som sagt i programmet ger detta oss nu 3^10 = 59049 möjliga kombinationer för de rätta svaren som ska testat istället för 4^10 = 1048576, nästan 18 gånger färre det vill säga! I termer av utvunnen information är det till och med lite sämre att få fem rätt, då man inte vet vilka fem det är och resterande fem kan varieras på tre sätt, så antalet kombos som fortfarande funkar är:
Noll rätt är dessutom riktigt bra att få tidigt, då framtida manipulationer av lådor kan bara göras på tre sätt istället för fyra (om man nu kommer ihåg de felaktiga alternativen, men vi utgår från perfekt minne här förstås).
Nu är det intressant att avgöra vilken taktik som snabbast ger en alla rätt om man bara chansar (och inte använder faktakunskaper man tror man besitter, hade vi kunnat någon fråga så hade vi nog inte fått noll rätt :)).
För enkelhets skull jämför vi två taktiker: att chansa på en låda i taget eller att chansa på två lådor i taget (och sedan förändra dem en och en för att få båda rätt). Att vända på lådorna tar ungefär lika lång tid som att att vänta på svar från programledaren, så det är det totala antalet ”försök” som avgör tiden det tar att testa sig fram.
Om man vänder på en låda i taget (och har tre alternativ som kan vara rätt), så är det en på tre att man gissar rätt och två på tre att man gissar fel. I det andra fallet behöver man max gissa en gång till, sedan kan man gå vidare till nästa låda, eftersom man vet vilket alternativ som är rätt. Det allra sista kontrollen kan vi alltså bortse från (försumbart). Således, väntevärdet på antalet försök är:
Gör man detta för två lådor, blir väntevärdet då lite mer än 3.
Om vi vänder två lådor i taget kan vi få tre alternativ: antalet rätt ökar med 2, med 1 eller med 0. Om två lådor är rätt behövdes det då ett försök, om en låda är rätt, så behöver man först vända en av dem för att bestämma vilken låda som var rätt (om man vänder på den som var fel kommer antalet rätt öka med 0 eller 1 (det senare fallet händer med mycket liten sannolikhet), annars minska), sedan kommer man antingen behöva testa noll/ett alternativ till (om man vände på den lådan som var fel) eller ett/två alternativ (om man saboterade den lådan som var fel från början). Om man har däremot 0 rätt från början så vänder man på båda lådorna igen och sedan behöver vända en eller två gånger till för att få båda rätt. Totalt blir väntevärdet ungefär följande:
vilket också är lite mer än 3!
Därför spelar det inte så stor roll om man testar en låda i taget eller två (och sedan fixar till lådorna en och en). I längden får man göra lika många försök i alla fall.
Sedan är ju frågan om man ska gå efter genomsnittsfallet (3 försök på båda strategierna), på värsta fallet (att man har maximalt otur) eller på det bästa fallet (att man har maximalt tur).
Första strategin (vända en låda i taget) har följande antal försök (innan man vet de rätta svaren) på vart och ett av fallen:
Värsta fallet: 5
Genomsnittsfallet: 3
Bästa fallet: 2
Andra strategin har följande:
Värsta fallet: 4
Genomsnittsfallet: 3
Bästa fallet: 1
Detta visar på att om man vill köra ”safe” så ska man satsa på andra strategin, då man behöver försöka färre gånger om man har otur. Men ointuitivt nog ska man också köra på den om man vill köra ”djärvt” och vill kunna klara pyramiden på färsta möjliga antalet försök. Den första strategin är helt enkelt för ”långsam”. Detta förutsätter att man har bra minne, men i övrigt tror jag båda lagen körde på den här strategin, vilket visar på en bra intuition för matematik och sannolikheter hos deltagarna.
Bombdesarmeringen
I andra tävlingen skulle lagen komma på ett kommunikationssystem för att kunna överföra siffrorna 0-9 och bokstäverna A-J utan ljud på ett långt avstånd till sina lagkamrater. För att inte hålla för mycket i huvudet kom båda lagen på ett system för antingen siffrorna eller bokstäverna och endast den typen skickades (gult lag skickade siffror, blått — bokstäver). Sedan översatte mottagarna på flotten: A=0, B=1, C=2 och så vidare. Detta system förutsätter att mottagarna inte till exempel råkar tänka att A=1. Effekten +/-1 är annars är ett vanligt fel vuxna brukar göra, till exempel när de programmerar eller beräknar antalet dagar i ett visst tidsintervall.
Systemet med siffror tyckte vi hade en fördel, eftersom uppgifterna gick ut på att få fram siffror, både i del 1 och del 2. Det hade varit lite extraarbete och osäkerheterna kommer in när man först ska översätta siffran till en bokstav, skicka bokstaven och sedan ska bokstaven översättas tillbaka till siffran i del 1. Men det verkade blå laget klara bra, det var inte det som var svårast, utan att lösa uppgifterna var det. Sedan är det ju en fördel i andra delen, att skicka bokstäverna direkt. I vilket fall blir det samma antal översättningarna för båda strategierna i andra delen.

När jag ändå pratar om osäkerhetsfaktorer, så är det just på grund av dem som det hade varit bra att skicka all information på en gång i andra omgången. Dykaren får veta fem bokstäver vars motsvarande kablar hen ska klippa. OM man räknat fel så finns det stor sannolikhet att kabeln med bokstaven inte ens finns. (OM man till exempel får två likadana siffror som svar så vet man redan på berget att man har gjort fel. Det vet man inte om man skickar en siffra i taget.) Då kan dykaren låta bli att klippa något och säga att en viss bokstav inte finns, vilket mottaggarna får försöka kommunicera tillbaka till räknarna.
Lag gult hann inte dock skicka ut någon information i del 2, utav vi fokuserade på att kontrollräkna istället då vi inte fick några likadana siffror.
Vad gäller del 1 så var det bra att skicka ett lås i taget, då man kan kolla just ett lås i taget (och inte en siffra i taget), om det är rätt, och kostnaden för fel är mycket mindre.
Här hittar du lösningar till alla uppgifter. Som jag nämner i det inlägget så kunde man löst uppgifterna på ett ännu smartare sätt, då man visste att svaret skulle bli en siffra. En smart lösning som min kompis Johan B tipsade mig till uppgiften
((√256 x 20 − 25^2 + 15^2 + 3^4) x 10) / 5 = ?
är följande:
Vi vill veta vilken siffra som resultatet är, därför räcker det att betrakta uppgiften ”modulo 10”, det vill säga studera slutsiffram i varje steg. Till exempel ser vi att vi har uttrycket (√256 x 20 − 252 + 152 + 34) x 2, därför kommer siffran att bli jämn. Och därför räcker att kolla vad uttrycket innan x 2 kommer att vara modulo 5. √256 x 20 slutar på 0 oavsett vad √256 är, därför kan vi strunta i att räkna ut det. − 25^2 + 15^2 är båda delbara med 5 och därför inte kommer bidra till sista siffran när man multiplicerar med 2 i slutet. 3^4 är det enda viktiga och vi kan räkna ut att det slutar på 1. Därför blir slutsiffran 1×2=2.
På liknande sätt kunde man ha gjort med kabel 3-uppgiften (försök själv!)
(15 – 7)(1500 – 25) – 2200 x 3 – 8^4 – 2^10 – 79 = ?

Pusselduellen
Det var svårt att se pusslen under programinspelningen, så vi roade oss med att räkna antalet kombinationer som varje pussel kunde vara i. Sedan gäller det förstås att hitta en bra sökväg mellan alternativen för att lösa pusslen snabbt.
Första pusslet består av sex bitar. Det var kanske givet vilken bit som skulle vara längst ner (om det inte var givet kunde man ta en godtycklig bit), så de resterande bitarna kan du placera på 5!*8^5 = 3932160 olika sätt (när du väl väljer en bit och en plats kan du vrida biten på 8 olika sätt vid den platsen, givetvis kommer de flesta sätt att direkt inte passa). Det är såklart inte rimligt att testa alla de sätten då en människa kan direkt se vad som passar och vad som inte passar. Ganska enkel brute force löser uppgiften i det här fallet.
Andra pusslet bestod av 18 bitar! Om man nu bara testar att lägga ner dem som en apa (utan att bry sig om hålen), så kan man göra det på 18!*4^18 sätt (varje pinne kan placeras på 4 sätt, em kombination av bak-och-fram eller inte och upp-och-ner eller inte), och det är för stort för att få plats i Google miniräknare-fönstret (storleksordningen 10^26)! Sedan kan man ha vissa symmetrier på hela konstruktioner, men det är bara en liten konstant som man delar med.
Man kan inte minska sökvägen jättemycket här heller, utan det finns väldigt många kombinationer ändå. Man får utgå från olika bitsorter och testa att starta på olika sätt. Inte konstigt att det tog lång tid…
Tredje pusslet är lättare än den andra, då det innehåller färre bitar. Här är tricket att börja med den största biten, den med mest volym och testa alla möjligheter för hur den kan sitta i den stora (än imaginära) kuben. Sedan ska den näst största biten in och så vidare. På så sätt kapar man sökträdet som bäst i början. Här är det svårt att uppskatta antalet kombinationer som behöver ”testas”, då pusslet har en mycket oregelbunden struktur.
Matematik i Genikampen – kluringar från tredje avsnittet
Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de alla.
Kodlås 1 bestod av tre uppgifter, där varje uppgift gav en siffra. Den tresiffriga koden skulle låsa upp det första låset under vatten.
Kodlås 2 gav på samma sätt ett tresiffrigt kod till andra låset.
Kablar 5 uppgifter gav 5 siffersvar, där 0 stod för A, 1 stod för B och så vidare till 9 som stod för J. Bokstäverna var kopplade till kablar som var safe att klippa av.
Kodlås 1
sifferkod 1
Sofie och Maria är syskon. För deras åldrar gäller följande samband: Summan är lika stor som produkten. Hur gamla är Sofia och Maria?
Addera talen.
Det här var enda uppgiften vi först gjorde fel på!
Den går ut på lista ut åldrarna S och M sådana att S+M = S·M.
Ekvationen S·M − S − M = 0 beskriver en hyperbel, som har oändligt många punkter. Men eftersom vi frågas efter heltalslösningar (och det bara ska vara en lösning som funkar), så funkar det bra att gissa.
Vi gissade på 0+0 = 0·0, men 2+2 = 2·2 funkar också. Det senare betraktas troligare som ålder (kanske säger man aldrig att någon är 0 år gammal), så svaret var 4 (och inte 0 som vi först trodde).
Första kodlåssiffran är 4.
sifferkod 2
En tjuv stal en säck med guldmynt i ett slott. För att komma ut ur slottet måste han passera tre vakter. Den första mutade han genom att ge vakten hälften av guldmynten. Vakten gav dock tillbaka 100 guldmynt av ren medkänsla. Den andra vakten fick hälften av tjuvens pengar men gav sedan tillbaka 50 guldmynt. Den tredje vakten fick hälften av pengarna men gav sedan tillbaka 25 guldmynt. Tjuven hade då 100 guldmynt kvar. Hur många mynt hade han från början?
Dividera svaret med 40.
Här är det lättast att gå baklänges. Tjuven hade 100 guldmynt i slutet.
Nu kollar vi hur mycket han hade innan varje händelse:
Innan tredje vakten gav honom 25 mynt hade han alltså 75 mynt (100-25).
Innan tredje vakten fick hälften av pengarna hade tjuven 150 mynt (75*2).
Innan andra vakten gav honom 50 mynt hade han 100 mynt (150-50).
Innan andra vakten gick hälften av pengarna hade han 200 mynt (100*2).
Innan första vakten gav honom 100 mynt hade han 100 mynt (200-100).
Innan första vakten fick hälften av pengarna hade han 200 mynt (100*2).
200/40 = 5.
Andra kodlåssiffran är 5.
sifferkod 3
Ett tåg består av ett lok och fem vagnar (A, B, C, D och E). På hur många sätt kan vagnarna ordnas så att vagn A kommer närmare loket än vagn B kommer?
Dividera svaret med antalet konsonanter i det svenska alfabetet.
Det går att ställa vagnarna på rad på 5! sätt. 5! står för uttrycket 5*4*3*2*1 = 120.
Detta beror på att en av de fem vagnarna kan ställas längst fram, en av de fyra kvarstående kan ställas på andra plats, en av de tre kvarstående på tredje plats, en av de två som är kvar kan ställas näst sist och ett alternativ har vi kvar för den vagnen som ska stå sist.
Exakt hälften av de ordningarna är sådana att A kommer närmare loket än B (och exakt hälften är tvärtom). Det beror på att alla ordningar kan paras ihop: varje ordning är i par med nästan samma ordning, fast där A och B har bytt plats. Till exempel är CADEB i par med CBDEA. Därför ska vi dela svaret med 2.
(Det här är för övrigt i stort sett samma uppgift som 2(a) här: LÄNK http://mattebloggen.com/wp-content/uploads/2014/09/Lektion2Permutationer.pdf)
120 / 2 = 60.
I det svenska alfabetet finns det 20 konsonanter (29 bokstäver totalt, varav 9 är vokaler).
60 / 20 = 3.
Tredje kodlåssiffran är 3.
Kodlås 2
sifferkod 1
Sofie satt på balkongen och gjorde sin matteläxa. Hon hade just skrivit svaret på en uppgift, när en duva kom flygande och lämnade sitt ”visitkort”, så att sista siffran (= entals siffran) i svaret inte syntes. Skillnaden mellan det ursprungliga svaret och det svar som nu syntes var 276. Vilket var det ursprungliga svaret?
Addera svarets siffror.
Om det ursprungliga slutsiffra var A, så kan talet skrivas som 10*X + A (oavsett hur många siffror talet har kan de skrivas som ett visst antal tiotal plus en slutsiffra).
När duvan har varit framme och busat hade Sofie talet X framme (antalet tiotal i det ursprungliga talet).
Det betyder att 10*X + A – X = 276
Det vill säga 9*X + A = 276.
Talet 276 är inte med i nians tabell, utan ger rest 6 när man dividerar med 9. Det betyder att A måste ha varit 6 och X i sin tur måste ha varit 30 (=270/9).
Så talet som stod där från början var 306 (=10*30+6). Detta är det enda svaret.
3+0+6 = 9
Första kodlåssiffran är 9.
sifferkod 2
Tre positiva heltal (naturliga tal) är så beskaffade, att om vart och ett multipliceras med de två övrigas summa, får man produkterna 120, 133 och 169. Bestäm talen.
Addera dessa tre tal och subtrahera det med det tal som kommer efter 13 i Fibonaccis talföljd.
Vi har tre tal som vi kan beteckna med a, b och c. Då vet vi att:
a*(b+c) = 120
b*(a+c) = 133
c*(a+b) = 169
Sen ska man bestämma talen står det, men det struntade vi i! Man skulle nämligen addera dessa tre tal senare, så vi fokuserade på att bestämma a+b+c (så man behöver inte bestämma vart och ett av talen).
c*(a+b) = 169. Eftersom 13*13 = 169 och 13 är ett primtal, går det bara skriva 169 som en produkt av tåv positiva heltal på två sätt:
169 = 13*13
169 = 1*169.
I det första fallet får vi att a+b+c = 13+13 = 26
I det andra fallet får vi att a+b+c = 1+169 = 170
Resan nu inser man att det är det första som är rätt (eftersom vi ska subtrahera 21 och få en siffra, men vi bevisar det korrekta svaret ändå utan att använda det).
133 = 7*19 och 7 och 19 är primtal, därav a+b+c är antingen 7+19=26 eller 1+133=134, så det måste vara 26!
(Detta stämmer även med faktoriseringen av 120 = 20*6 till exempel. Nu kan vi bestämma a, b och c för sig men det är för mycket jobb).
Fibonaccis talföljd är 1,1,2,3,5,8,13,21,34 och så vidare. Varje tal från och med det tredje är lika med summan av de två talen innan. Läs coola grejer om Fibonaccitalen
26 – 21 = 5
Andra kodlåssiffran är 5.
sifferkod 3
((√256 x 20 − 252 + 152 + 34) x 10) / 5 =
Det här är bara en vanlig uträkning. Men man kan ändå räkna ut det lite smart:
Då 256 är 2 upphöjt till 8, så är roten ur det 2 upphöjt till 4, det vill säga 16.
Multiplicerar man den stora parentesen med 10 och sedan dividerar med 5, så är det samma sak som att multiplicera parentesen med 2.
Sedan räknar man ut potenserna.
Då får man följande uttryck och du kan följa lite hur man kan tänka för att räkna snabbare:
(16*20 – 625 + 225 + 81)*2 =
(320 + 225 + 81 – 625)*2 =
(320 + 306 – 625)*2 =
(26 – 25)*2 =
1*2 = 2
Tredje kodlåssiffran är 2.
Kablar
Kabel 1
(6y-7)/4 + (3y-5)/7 = (5y+78)/28
Vad är y?
Detta är en vanlig ekvation, dessutom ser man att 28 är en minsta gemensam multipeln till 4 och 7, så det lättaste är att få bråken till gemensam nämnare:
7*(6y-7)/28 + 4*(3y-5)/28 = (5y+78)/28
Nu kan vi glömma bort 28:
7*(6y-7) + 4*(3y-5) = (5y+78)
Multiplicerar in talen:
42y – 49 + 12y – 20 = 5y + 78
Förenklar:
42y + 12y – 5y = 78 + 49 + 20
49y = 147
7y = 21
y = 3
Första kabeln ska ha bokstaven (3=)D.
Kabel 2
I herrtruppen till VM i cykel hade lagledare Hjulström tagit ut cyklister från enbart två klubbar – lika många från varje klubb. När det var dags för lagtempo, visade ett testlopp att alla åkarna i stort sett var jämngoda.
Hjulström beslöt därför att ta med två cyklister från vardera klubb i lagtempolaget. Ändå gav detta inte mindre än 36 tänkbara lagsammansättningar! Hur många cyklister bestod truppen av?
Den här uppgiften var inte det lättaste att tolka, så vi försökte tolka på ett sätt som skulle ge ett ensiffrigt svar.
Vi vet att det finns n cyklister i var och en av de två klubbarna. Om man ska räkna hur många sätt det finns att välja två stycken ur en klubb får man det från uttrycket n*(n-1)/2 (n sätt att välja den första, n-1 sätt att välja den andra, dela med två för att ordningen på de inte spelar roll, precis samma idé som i vagnuppgiften).
För att få antalet sätt att sätta ihop laget måste man multiplicera sätten att välja två från första klubben och två från andra klubben, vilket ska ge 36. Då n är densamma för båda klubbarna, innebär det att det ska finnas 6 sätt att välja två pers från en av klubbarna (för att 6*6=36).
Nu får vi uppställningen n*(n-1)/2 = 6, vilket betyder att n*(n-1)=12, så n måste vara lika med 4.
Så då är frågan om vi ska svara 8 eller 4. Troligen 8 eftersom det verkar som att man räknar in båda klubbarna i truppen.
Andra kabeln ska ha bokstaven (8=)I
Kabel 3
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
En vanlig uträkning till! Tur att man kan sina tvåpotenser:
210 = 1024
84 = (23)4 = 212 = 4096
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
8*1475 – 6600 – 4096 – 1024 – 79
Egentligen kan man bryta ut 8:an på tre ställen för att slippa räkna en stor multiplikation:
8*1475 – 8*825 – 8*512 – 8*128 – 79 =
= 8*(1475 – 825 – 512 – 128) – 79 =
= 8*(650 – 512 – 128) – 79 =
= 8*(138 – 128) – 79 =
= 8*10 – 79 =
= 80 – 79 =
= 1
Tredje kabeln ska ha bokstaven (1=)B
Kabel 4
Lille Micke sålde två fotbollskort för 21 kronor.
På det ena kortet tjänade han 10 % och på det andra kortet förlorade han 10 %.
Allt som allt tjänade han 5 %. Hur mycket hade varje fotbollskort kostat i inköp?
Svar: Addera dessa två tal och dividera summan med
den fjärde decimalen i pi.
Ett av de (till synes) svårare problemen! Lätt att virra ihop sig med procent. Men precis som i kodlåsproblemet med primtal behöver man inte lösa hela uppgiften. Vi ska ju använda summan av ursprungspriserna sedan, därför behöver vi egentligen inte ta reda på vart och ett av priserna, utan på vad det var tillsammans.
Om korten hade kostat A och B från början kan vi skriva villkoren som
21 = 1,1*A + 0,9*B = 1,05*(A + B).
Men om det är A+B vi är ute efter är uppgiftens andra rad helt onödig! Vi har:
21 = 1,05*(A + B)
A + B = 21/1,05 = 2100/105 = 300/15 = 100/5 = 20.
Och tur att man kan lite pidecimaler! 3,14159… Så svaret ska divideras med 5. 20/5 = 4.
Fjärde kabeln ska ha bokstaven (4=)E
Kabel 5
Då ett visst fyrsiffrigt tal multipliceras med fyra, får man ett nytt fyrsiffrigt
tal, där sifferföljden är omvänd jämfört med det första talet,
dvs. 4*ABCD = DCBA
Vilket är det ursprungliga talet?
Subtrahera svaret med 2004 och dividera den summan
med det tionde primtalet.
Här berättar jag en stor del av lösningen i tv. Men nu har jag chansen att kortfatta lösningen.
A = 1 eller 2, annars blir inte talet DCBA fyrsiffrigt. Då HL är jämnt, måste A = 2.
Då är D = 8 eller 9, annars är HL för litet (VL är minst 4*2000). Då 4*D ska sluta på A måste D = 8.
Vi har då 4*2BC8 = 8CB2.
Om vi fortsätter uträkningen med tiotal måste 4*C + 3 sluta på B. Samtidigt får inte B vara för stort (måste vara mindre än 3) för att multiplikationen 4*B00 inte ska ge ett till tusental.
Vi testar med olika C (i uppgiften är det inte givet att siffrorna A,B,C och D är olika även om det brukar vara så i sådana rebusar):
4*C + 3 = (”slutar på”) B
4*0 + 3 = 3 – för stort
4*1 + 3 = 7 – för stort
4*2 + 3 = 1
4*3 + 3 = 5 – för stort
4*4 + 3 = 9 – för stort
4*5 + 3 = 3 – för stort
4*6 + 3 = 7 – för stort
4*7 + 3 = 1 –
4*8 + 3 = 5 – för stort
4*9 + 3 = 9 – för stort
Då vet vi att B måste vara 1 och C är antingen 2 eller 7. Vi testar med båda:
4*2128 = 8512 – passar inte.
4*2178 = 8712 – passar!
Nu räknar vi ut kabelbokstaven:
2178 – 2004 = 174
Tur att man kan lite primtal: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…
Det tionde primtalet är alltså 29.
174/29 = 6 (egentligen hade man kunnat gå från slutet och testat de tio olika ursprungstalen 2004+0, 2004+29, 2004+29*2 och så vidare, men det är lätt att vara efterklok).
Fjärde kabeln ska ha bokstaven (6=)G
Vi var klara med uppgifterna lite innan motståndarbomben smällde (men höll på att kontrollräkna)!
Gillade du för övrigt sifferrebusen, kan du kolla upp några lite svårare här på bloggen: Granrebus, Sifferrebus, Palindromrebus och Trigonometrisk rebus.
Matematik i Genikampen – första avsnittet
I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.
Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror att detta har gjort mig smart på flera sätt, inte bara bra i huvudräkning. Matte för mig är så mycket mer än att räkna och därför vill jag visa nedan hur man kan tänka på ett matematiskt sätt även när man inte ”räknar”. Matte för mig handlar om att tänka.

Orientering på sträcka
Tävling ett börjar med att vi blir uppdelade i lag med 6 personer i varje. Uppgiften är att orientera i skogen, det vill säga passera 4 kontrollpunkter innan man kommer fram till målet. Laget får en karta, men ingen kompass. Det gäller att göra detta inte på kortast tid, utan på kortast sträcka! Två personer i laget har GPS-sändare, som sträckan mäts på, men även de andra 4 personerna i laget ska hålla ihop med personerna med GPS, ingen får ”scouta” framme. (Överlag fick deltagarna veta reglerna i detalj och även fick ställa förtydligande frågor, vilket inte visas i tv.)
Jag antar att man tar medelvärdet av de två GPS-positionerna för att få fram banan för att sedan mäta avståndet. Vi fick veta att om avståndet skiljde sig med mindre än 50 m, så var det tiden som gällde. 50 m var så pass lite i sammanhanget (man gick kanske i 35 minuter), så det rätta valet var att strunta totalt i tiden och fokusera på att gå precis kortast.
Hur hjälper matten här då? Jo, man bestämmer att personerna med GPS-sändarna måste gå så rakt som möjlig (DUH!). Detta löser man genom att de inte går först, utan i mitten eller sist. Då kan de personerna som går först gå lite fel (och på så vis ”scouta”). Om personerna som går först går längs med kateterna i en rätvinklig likbent triangel med kateterna 3 m, så kommer personen med GPS:en gå ”bara”
4,24 m istället för 6 m alltså! En vinst på 1,76 m! Sker detta 100 ggr, vilket var rimligt för banan, så vinner man redan 176 m på att gå så. Pythagoras sats ftw!
Givetvis är detta egentligen en försumbar optimering i jämförelse med att ”gå rätt”, vilket sätter orienteringsskills över matten i det här fallet. Så är det ibland, men lite bidrag från olika sätt att tänka här och var är sånt som avgör tävlingarna.

Orientering på tid
Andra delen av första tävlingen gick ut på att orientera på ett fabriksområde och hitta halvgömda kontoller. I kontrollerna fanns ledtrådar, mer om dem senare. Här hade gula laget 3 minuters försprång, vilket visade sig inte bara hjälpa, utan stjälpa.
Det fanns nämligen i princip två optimala sätt att ta kontroller (med kortast sträcka): medurs eller moturs (ordningen för kontrollerna blev ganska naturlig), eftersom man skulle tillbaka till samma ställe. Gula laget började, men eftersom blåa laget följde samma riktning, kunde de spara tid på att inte leta efter kontroller, utan observera det gula laget när de var precis ikapp, men lite efter. Det hade blivit annorlunda ifall det blåa laget hade valt motsatt riktning, då skulle förmodligen inget lag få fördel (eller i alla fall är den förväntade fördelen lika) av att vara ”efter”. Banorna skulle korsa varandra i ungefär mitten och då skulle det blivit mer ”rättvisst”. Lite kul ändå att slumpen påverkar!
Uträkningar
Sista delen av första tävlingen gick ut på att göra uträkningar (Genikampen kallar det ”lösa ekvationer”, men jag håller inte med om den termen, eftersom ”ekvationer” för mig förutsätter ett närvaro av ett ”lika med”-tecken och någonting okänt.) Om uppgifterna görs i fel ordning (det vill säga, man försöker få ett resultat utan att veta att KATT = 2 och HARE = 5), så kan man inte få ett svar, men man kan förenkla uttrycken. Gula laget öppnade just ett uttryck med okända först (och visste ju inte vad som väntade), så det enda som fanns i början var att förenkla, vilket gjorde att man kunde räkna ut resultatet av det uttrycket snabbare efteråt.
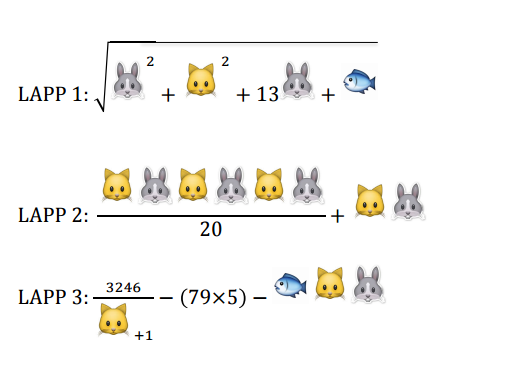
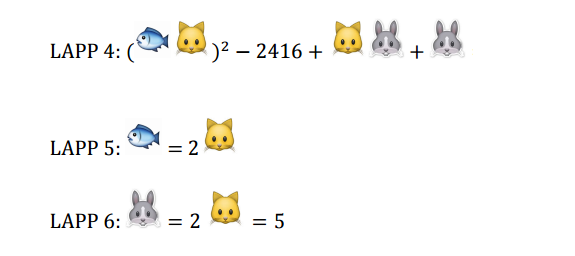
Som sagt, beräkningar är inte allt som matte är. Nu råkar jag vara snabb på att göra aritmetiska beräkningar, men kanske hälften av de verksamma matematiker jag träffar är inte bra på snabba beräkningar alls. Det är lite som att vara bra på Rubiks kub: Man har antingen lärt sig det eller inte. Man kan vara smart på knep & knåp utan att vara bra på Rubiks kub. Jag skulle inte heller säga att de som är bra på huvudräkning är automatiskt bra på matte, även om man förmodligen är bra på att se mönster, vilket hjälper en att räkna snabbare. Överlag, de som är bra på räkning är personer som är så pass lata att de vill göra det snabbt :)
Testa dig själv på tid om du tycker att det är kul att räkna.
Paintball-quiz
Andra tävlingen gick ut på att ha paintball-dueller med frågesport. Inte jättemycket matte, men man kan fundera över taktiken matematiskt. Det gäller att bedöma sina chanser att träffa vid skjutningen samt chanser att svara rätt på frågan. Om du inte är säker alls på att träffa (t.ex. Valentina som aldrig har sjutit/träffat i sitt liv) bör du skjuta snabbt om det är liten sannolikhet om din motståndare träffar. Med stor sannolikhet missar båda och då har du i alla fall första tjing på frågan. Men det kan också vara dumt att svara först om du t.ex. funderar mellan två alternativ: Då kan det vara bra att motståndaren eventuellt kan utesluta ett av alternativen genom att svara fel. Men den situationen händer typ aldrig.
Om man däremot är bra på att träffa bör man förmodligen börja med att undvika skottet från motståndaren och sedan skjuta själv i lugn och ro. Detta kan ge en säkra poäng, samt chansen att svara först!
Givetvis kan motståndare av liknande ”typ” träffar varandra, vilket resulterar i symmetrisk strategi och en Nash-jämvikt, men det är inget man hinner tänka på när man står där framme :) Då blir det lite kaotiskt och återigen slumpen som avgör.
Ordbygge
Duellen gick ut på att forma ord. Ser man inte färdiga ord så är det brute force som gäller (dvs testa alla möjligheter: Vilken kub är först, vilken är tvåa, hur ska tvåan vara vriden, etc.). Under antagandet att alla bokstäver är unika får vi
uppställningar av tre kuber, eftersom kuberna kan ordnas på 6! = 3 sätt och roteras på 4^3 sätt. Men sedan kan varje uppställning ”visas upp” på 4 sätt (genom att ha ett av de fyra orden framme), så därför delar man med 4. Tycker du sånt här med att räkna sätt är skoj, kolla upp en lektion i kombinatorik som jag har lett.
På samma sätt kan man räkna ut att fyra kuber kan ordnas på
sätt och fem kuber på
sätt (under förutsättningen att alla bokstäverna är unika). Antalet sätt halveras ungefär för varje par av likadana bokstäver, men den storleksordningen blir det i alla fall.
Såklart är det mänsikligt omöjligt att testa alla sätt på begränsad tid, men lyckligtvis behöver man det inte, eftersom man kan utesluta massa fall, för att det ska ju bildas ord. Till exempel, om ordet börjar på ett ”T”, så kan inte andra bokstaven vara ”N” och den insikten sparar en 3!*4^3 = 384 fall. Så det var ju mänskligt att lösa det sista pusslet, även om det tog lång tid. Tricket är ändå att se ett ord som är med och anpassa kubuppställningen efter det. För mig var det att se början ”AO” som fick mig att tänka på ”AORTA”, som då senare gav två möjliga uppställningar av kuben, vara den ena var rätt (gav ord även på de andra sidorna: ”LIVET”, ”KENYA” och ”TITAN”).
Tresiffriga tal
Tresiffriga tal
Första hemuppgiften från Matteklubben, åk 5-6
Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.
• Hur många olika armband kan man tillverka av 3 svarta och 2 vita pärlor? På bilden har du ett exempel.
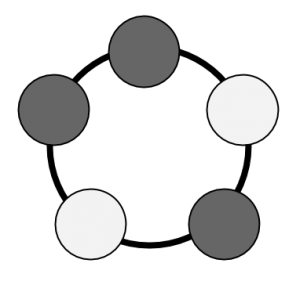
• Hur många svart-vita armband med 5 pärlor kan man tillverka överhuvudtaget?
• Hur ändras svaret om antalet pärlor får vara större?
Första träffen med Matteklubben, åk 5-6
Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Här på bloggen tänkte jag lägga ut materialet som vi tar upp på träffarna, samt skriva lite om hur lektionen har gått.
Träffen började med att eleverna tog fika och satte sig ner i ett stort klassrum. Nästan alla de ordinarie platserna blev upptagna (41 stycken). Vi var sju lärare och jag presenterade vad alla hette. Nästan direkt satte vi igång med de blandade uppgifterna. Det enda eleverna behövde var penna och kladdpapper, som de fick låna.
Eleverna fick dela upp sig i grupper om två-tre och i ungefär i 45 minuter försöka lösa fem uppgifter. När de hade löst en uppgift fick de räcka upp handen och berätta lösningen för en av lärarna. Läraren kunde då ställa följdfrågor, som att t.ex. be om att förklara svaret eller fråga om varför det är det enda möjliga svaret.
Under varje uppgift skriver jag några typiska dialoger jag hade med de små grupperna om just den uppgiften.
Blandade uppgifter
1. En pojke har lika många systrar som bröder, men hans syster har hälften så många systrar som bröder. Hur många pojkar och flickor finns det i familjen?
Elev: Hur kan man lösa den här uppgiften när det inte finns några siffror?
Lärare: Försök att pröva dig fram!
Elev: Vi fick att det var 4 pojkar och 3 flickor. Det uppfyller villkoren.
Lärare: Varför kan det inte finnas något annat svar?
2. I tre högar finns 22, 14 respektive 12 nötter. Du får göra tre förflyttningar. Ditt mål är att få högarna att innehålla lika många nötter.
Under en förflyttning får du flytta ett antal nötter från en hög till en annan, men antalet nötter man flyttar måste vara lika med antalet nötter i högen man flyttar till.
Vilka förflyttningar ska du göra?
Elever: Går det här verkligen att göra?
Lärare: Ja :D
Elev: Vi försöker med olika varianter men lyckas inte. (Förklarar hur de tänker.)
Lärare: Vad händer om du tänker baklänges? Vad skulle det sista draget kunna vara?
3. Skriv en siffra till vänster och en siffra till höger om 15 så att det nya talet blir delbart med 15 (det vill säga blir ett tal där divisionen med 15 går jämnt upp).
Elev: 0150, gills det?
Lärare: Försök att hitta på fler svar. (Alternativ: Nej, tal kan inte börja med 0.)
4. På den största ön i Sagolandet finns 4 kungadömen. Varje kungadöme gränsar till de tre andra. Rita karta över ön så som den kan se ut.
Elev: Till exempel så här (visar en cirkel uppdelad i fjärdedelar.)
Lärare: Vi räknar det inte som en gräns om de bara nuddar varandra på hörn, eftersom man inte kan gå över från ett land till ett annat. (Alternativt: Försök att hitta på fler svar.)
5. I en sjö har man placerat en väldig ovanlig vattenlilja. Varje dag så fördubblar liljan sin storlek.
Det visade sig att liljan tog upp precis hela sjön efter 20 dagar. Efter hur många dagar skulle sjön ha blivit full om man hade placerat ut 4 magiska vattenliljor från början?
Elev: Om det tog 20 dagar för 1 lilja, så borde det ta 20/4 = 5 dagar för 4 liljor.
Lärare: Låt oss undersöka om din logik fungerar i andra situationer. Om det hade tagit 4 dagar för en lilja att fylla sjön, så borde fyra liljor göra det på 1 dag, eller hur? (Undersöker lite och kommer fram till att det är 2 dagar i det fallet.)

Det fungerade väldigt bra att kommunicera med eleverna, vi var lagom många lärare (i snitt 5-6 elever per lärare) och ett par grupper hann precis klara av alla 5 uppgifterna när 45 minuter hade gått.
Därefter gick vi igenom varje uppgift på tavlan. En elev fick komma fram och förklara sin lösning och vi försökte alltid att diskutera alternativa lösningar. På uppgift nummer fyra fick alla gå fram och rita sina karta, vi fick väldigt många snygga exempel.
Därefter var det en liten-liten rast och vi skulle komma igång med temat, vilket var kombinatorik. Eleverna fick sitta i grupper om 4-6 och tänka och experimentera med hjälp av färgpennor. Denna gång försökte vi kommunicera med hela gruppen på en gång. Eleverna jobbade i grupp i ca 45 minuter, därefter var det 15 minuter gruppdiskussion.

Innan eleverna satte igång gick vi igenom färgerna som OS-ringarna har och att det har att göra med att alla länder i världen har någon av dessa färger i sin flagga. Därför skulle vi rita olika flaggor med de fem färgerna, men flaggorna behövde inte existera på riktigt.
Flaggor
1. Hur många olika flaggor av följande form kan man skapa om man har tillgång till fem färger?
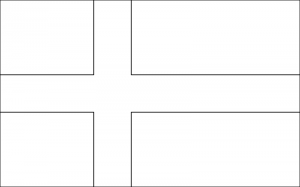
Här förtydliga vi på tavlan att alla de fyra rektanglarna måste ha samma färg. Det dök upp en intressant fråga om korset fick ha samma färg som bakgrunden. Då bestämde vi att man kunde lösa två olika problem, ett där de fick ha samma färg och ett där de inte fick.
Eleverna löste det här på flera olika sätt som genomgången visade (när vi tänker på varianten då de inte fick ha samma färg).
Om korset får vara en av de fem färgerna, så kan bakgrunden ha fyra varianter för färg. Det är likadant för alla fem färgerna på korset. Alltså är svaret 5*4 = 20.
Om man tar två färger, till exempel blå och svart, så kan man göra två flaggor: En med svart kors på blått bakgrund och en med blått kort på svart bakgrund. Det finns 10 olika par av färger (man skriver upp alla möjligheter och kollade att man inte missade något.) Alltså är svaret 10*2 = 20.
Om man får ha samma färg på korset som på bakgrunden, så är svaret 25 (= 5*5). Men man måste räkna bort de enfärgade flaggorna, som det finns precis 5 av, lika många som färger. Alltså är svaret 25 – 5 = 20.
2. Hur många olika flaggor av följande form kan man skapa om man har tillgång till fem färger?

Här dök det också upp frågor om olika varianter: var alla räderna tvungna att vara olika? Fick översta och nedersta vara samma? Fick alla ha samma färg? Vi bestämde oss för att lösa tre olika varianter.
Variant 1: Alla ränderna måste ha olika färger. Några grupper listade ut hur man skulle räkna ut det och tillsammans på tavlan kom vi fram till att svaret blir 5*4*3 = 60.
Variant 2: Översta och understa ränderna får ha samma färg. Någon enstaka grupp listade ut svaret här också. Vi kom fram till att man skulle lägga till något antal till svaret i Variant 1. Man kunde tänka att när understa och översta randen är likadana så är det precis samma situation som med svenska flaggan (mittersta randen är korset, resten är bakgrunden). (Det var en elev som kom på det). Alltså är det 20 varianter vi måste lägga till, så att svaret blir 60 + 20 = 80. En annan elev kom på att vi från början kunde räkna 5*4*4 = 80.
Variant 3: Ränderna får ha vilka färger som helst. Ett par grupper räknade ut att det var 5*5*5 = 125.
Tillsammans på tavlan kom vi fram till att vi behövde lägga till 20 + 20 + 5 till Variant 2 (flaggor där översta och mellersta randen är lika, flaggor där understa och mellersta är lika och flaggor där alla ränder är lika). 80 + 45 = 125 – ett annat sätt att få svaret! Men då tog tiden slut!
3. a) På hur många sätt kan ni i er grupp ställa er på en rad?
b) På hur många sätt kan ni bilda en ring?
Några av eleverna hann testa på den här uppgiften. En del kom fram till rätt svar på a)-uppgiften. Svaren var olika beroende på hur många de var (4,5 eller 6). Men många fick samma svar på b) som på a). Då kom jag med följande invändning:
Lärare: På hur många kan två personer ställa sig på en rad?
Eleverna: Två!
Lärare: På hur många sätt kan två personer ställa sig i en ring?
Eleverna: Ett! Hmmmm…
Lärare: Varför skulle det då vara samma svar för fyra/fem/sex personer?
Uppgiften hann vi tyvärr inte diskutera i helklass, så den tar vi upp nästa gång.
Allt som allt gick lektionen bra för att vara i en så enorm klass. Eleverna blev trötta mot slutet, så nästa gång kommer vi ta en lite längre rast. Det vore också kul om eleverna interagerade mer mellan olika skolor och då kan det vara bra med slumpvis fördelade grupper, som vi kör en mattetävling emellan.
Jag ser fram emot att träffa alla eleverna om fyra veckor! Det är väldigt kul att hålla på med matte med elever som har väldigt god förståelseförmåga. Elever som är inte rädda för att försöka och därför lyckas väldigt bra med att lösa problem som jag är säker på att inte så många vuxna skulle klara.
En lektion för små barn i kombinatorik
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Kombinatorik
Kombinatorik är läran om kombinationer och permutationer, men för mig är det helt enkelt ett grundläggande tankesätt när man håller på med problemlösning. När du till exempel väljer vad du ska ha på dig på en festkväll är det kombinatoriken som säger om du har testat alla … kombinationer.
Samma teori hjälper dig när du lägger pussel. Kombinatoriken hjälper dig att testa de likadana ljusblå bitarna till himlen systematiskt istället för att bara slumptesta. Problemet löses snabbare och du är säkrare på att du har löst det!
Vissa av mina matematiker älskar kombinatorik, vissa ser det bara som ett oundvikligt redskap. Själv är jag väldigt tacksam för att min pappa lärde mig kombinatorik tidigt, redan vid 11 års åldern ungefär.
Om du är osäker på vad ämnet innebär rent praktiskt, kolla aktiviteterna nedan. Lekarna skall tjäna som en slags introduktion till ämnet.
Uppdrag med gubbar och hus
För att leka uppställning i olika rader och ringar är det bra att ha likadana objekt i olika färger. Så varför inte spelgubbar?
Jag plockade fram spelet Arkadia ut hyllan och upptäckte massa potential i spelkomponenterna:

På bilden ser ni gubbar i fem olika färger (jag kommer använda 11 i varje färg), torn som går att stapla på varandra, olika slags pengarbrickor, tetrisliknande brickor och kort. Längst bak till vänster ser ni ”tält” som det går att hänga upp små flaggor på.
Vi ska leka ”Köpmännens stad”, där barnen får svara på olika svåra frågor eller utföra olika svåra uppgifter (beroende på vad det är för ålder). För varje klarat uppdrag hängs en flagga upp. Målet är att ha så många flaggor som möjligt uppe.
5 år
För de minsta barnen handlar kombinatorik om att räkna, gruppera och jämföra. Följande uppgifter kan vara lämpliga:
– Gubbarna står i olika grupper. Hitta en siffra som motsvarar antalet gubbar i gruppen (1,2,3,4 etc.) och lägg den bredvid gruppen. Vilken grupp är störst? Vilken är minst?
– Vilka är fler: de gröna eller de gula gubbarna (lösningen är att para ihop dem, en gul med en grön och se om någon sort blir över)?
– Arrangera alla gubbarna (det är 55 stycken) i trianglar, så att hörnen ugörs av var sin gubbe. Arrangera gubbarna i cirklar. Arrangera gubbarna i en jättestor rektangel, om det går.
– Varje gubbe ska få var sitt mynt. Plocka fram så mycket mynt, som gubbarna skall ha tillsammans (5- och 10-myntbrickor får användas).
– Nu går gubbarna hem. Kan ni placera dem i grupper så som de var i början? (Siffrorna 1,2,3,4 etc. ligger kvar och hjälper till).
6 år
Några frågor kan vara samma som för femåringarna. Dessutom är det dags att börja med riktiga kombinationer.
– Gubbarna bestämde sig för att prata med några nya människor (köpmän av annan färg). Kan man dela upp gubbarna i par så att alla är med någon annan färg (Svar: alla utom en gubbe går att dela in i par)?
– Nu skulle gubbarna bilda lag, där tre olikafärgade köpmän skulle ingå. Hur många olika sortes lag kan bildas (Svar: 10 stycken)?
– Kan de tio lagen ställas ihop i en stor ring, så att inga två gubbar av samma färg står bredvid varandra?
– Efter att barnen ställer tillbaka gubbarna så som de stod i början, plockar jag bort några stycken under tiden som barnen blundar. Sedan skall barnen titta på bordet och försöka lista ut hur många jag tog bort.
Efter uppdragen kan vi röra på oss lite. Barnen, uppdelade i två grupper, ställer sig i en ring. Sedan skall de byta plats inom sin grupp så att det inte blir samma ring som förut. Hur många olika ringar kan bildas? (Svar: är de 3 stycken, finns det 2 olika ringar, är de 4 stycken, finns det 6 olika ringar.)
7 år
En del uppdrag lånar jag från sexåringarna, speciellt det sista om ringar. Med med sjuåringarna anteckngar vi de olika ringarna mha gubbarna i olika färger. Andra uppgifter kan vara:
– Hur många gubbar är det totalt? Gubbarna/siffrorna får grupperas om för att det skall vara enklare att räkna.
– Nu står det rätt antal gubbar i varje rum, men inte alla har rätt färg. Går det att återställa situationen i början, genom att man får gå en gubbe i taget? Om en gubbe går in i en grupp och det blir för många gubbar i gruppen, måste en ny går ur gruppen och fortsätta vidare på samma sätt. Matematiskt handlar det om att faktorisera en permutation i en produkt av cykler. Vilket alltid går.
– Vilket antal små torn går att bygga ihop till en stor triangel? (Svar: 1,3,6,10 osv. Dessa tal kallas just ”triangeltal”.)Är totala antalet gubbar ett triangeltal? (Svar: ja)
– På hur många sätt kan ni ställa er på en rad? Kan ni hitta på en egenskap för varje sätt? (T.ex.: länggordning, bokstavsordning etc.)
10 år
Frågorna om triangeltal, rader och ringar är som för sjuåringarna. Förutom det får tioåringarna problem i stil med:
– Kan 6 gubbar ställas ut på planet, så att det är 2 stycken vid varje kant?
– Kan gubbarna arrangeras om, så att antalet är detsamma (1,2,…,11), men färgerna är så olika som möjligt. Kan det vara så att det högst är 2 gubbar av varje färg i en och samma grupp? (Svar: nej, enligt lådprincipen måste gruppen med 11 personer innehålla minst 3 av samma färg.)
Pussel
Efter väl avklarade uppdrag skall vi göra gamla hederliga pussel. Förutom att det inte finns någon bild och formen på bitarna är oregelbunden!
Minne
Ett välkänt spel som tränar minne är att en person säger ett ord. Till exempel, om kategorin är ”saker i rummet” kan första personen säga ”bord”. Den andra personen måste då säger det förra ordet, samt ett ord till: ”bord, tavla”. Nästa säger ”bord, tavla, dator”. Och så fortsätter man tills någon gör fel: glömmer bort ordningen eller orden, eller säger ett ord som redan har sagts. Då kan man byta kategori.
Den här leken passar stora som små och tränar både språk, minne och kategorisering.
Einsteins pussel
De äldre barnen är mogna för ett logikpussel. Sjuåringarna får klura på ett 3×3-pussel, de äldre kan ta sig an något i stil med 5×4.
Kombinatorik i Futurama

En mörk eftermiddag hade ett gäng studenter samlats för att kolla på – ni gissade rätt – Futurama! Ljuset släcktes, stora platt-teven slogs på och alla förberedde sig för att mysa under filtarna till favoritserien.
Det kanske bör nämnas att rummet de satt i hade en stor whiteboard, och att studenterna pluggade matematik …
Så vad händer när halva serien har gått? Jo, ljuset är på, avsnittet pausat och flera personer står och skriver egna siffror på tavlan. Varför?
Ni förstår nog om ni tittar på avsnittet ”The Prisoner of Benda” (säsong 6, episod 10) själva. Det innehåller nämligen ett kombinatoriskt problem som är väldigt viktigt för karaktärerna att lösa!
Varning: handlingen spoilas lite nedan!
Professorn uppfinner nämligen en maskin, som kan byta plats på medvetanden hos två människor (detta åskådliggörs genom att varje kropp får den andra kroppens röst).
Professorn och Amy byter plats, för att han vill en stund kunna leva i ett ungt kropp igen medan hon vill kunna äta lite extra. Men när de vill byta tillbaka så går det inte! Maskinen låter inte två kroppar byta med varandra igen om de någonsin har bytt förut!
Bender tror att han hjälper till att lösa problemet och byter sitt medvetande med Professorns (och får då Amys kropp). Nu börjar det bli ganska rörigt eller hur?
Så hur ska våra vänner komma tillbaka till sina egna kroppar? Kom ihåg att inga två kroppar får byta medvetanden med varandra fler än en gång.
Saker kompliceras ytterligare sedan i avsnittet genom att fler och fler par personer byter. Hur löses problemet i allmänhet om en grupp på n personer har trasslat till sig genom en massa byten? Vilket blir det minsta antalet byten för att återställa allt?
Så när du kollar på avsnittet, bli inte förvånad om någon vill pausa mitt i och ta fram papper och penna, om du har en gåtälskare i sällskapet.

