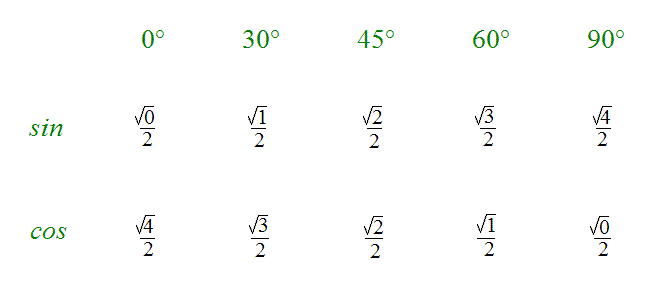Det finns vissa saker som man bara måste lära sig utantill. Det kan tyckas att det är det enda som gäller i matten, men det kan räcka ganska långt att kunna bara några få formler.
Till exempel så kan vi prata om trigonometri. Jag tänkte dela med mig lite tips om hur man bäst kommer ihåg det essetiella och hur det går att härleda allt det viktiga därifrån.
För det första måste man lära sig vad sinus och cosinus är för någonting.
Båda två är funktioner som ger ut ett tal, när man stoppar in en vinkel. Men vad är det för tal? När vinkeln är känd (och mindre än 90 grader), så kan vi rita en rätvinklig triangel med den vinkeln. Låt oss säga att vår vinkel kallas för x. Det går förstås att rita flera olika stora rätvinkliga trianglar med x, men det kommer inte spela någon roll.
Vi mäter sidorna på vår uppritade triangel och konstateterar att kateterna är a och b långa och hypotenusans längd betecknar vi c. Då är sinus värde lika med den motstående kateten genom hypotenusan och cosinus är den närliggande kateten genom hypotenusan. Alla likformiga trianglar har samma förhållande mellan sidorna, därför spelar det ingen roll vilken storlek på triangeln vi väljer.
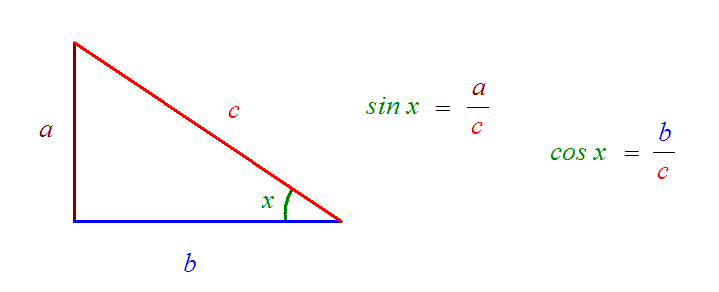
Men hur ska man komma ihåg vilken funktion som är vilken om man nyss har lärt sig dem? Tänk på att cos (cosinus) låter lite som ”kossa” och kossan den är lat, därför vill den vara nära sin vinkel (orkar inte gå till motstående sidan). Och sin är då den andra funktionen.
Ett annat sätt att komma ihåg det är att sinus är snäll och cosinus är elak. Så sinus offrar sig och går till den motstående sidan. Fler tecken på sinus snällhet och cosinus elakhet kommer vi se i del 2.
Om du nu kan lite vanlig geometri är det inga problem att räkna ut sinus och cosinus för flera kända vinklar! Här väljer jag att mäta vinklarna i grader.
De saker som du behöver kunna är:
– Pythagoras sats
– vad vinkelsumman i en triangel är
– att likbenta trianglar har basvinklarna lika
– att trianglar med lika basvinklar är likbenta
Vi kan då räkna ut vad sinus för vinkeln 30° är, om man inte minns det. Rita såklart först en rätvinklig triangel med en vinkel lika med 30°. Och eftersom vinkelsumman för vilken triangel som helst är 180°, så är den sista vinkeln lika med 180°-90°-30° = 60°.
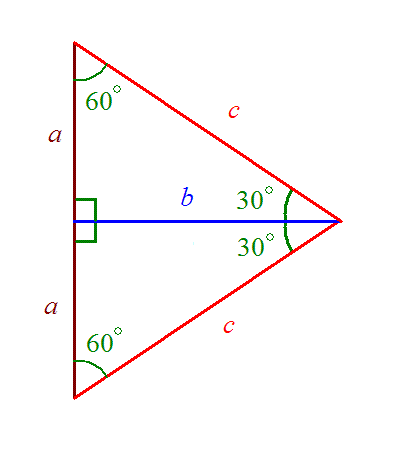
Rita sedan upp en likadan triangel, fast spegelvänd, och för ihop halvorna. Det som bildas är förstås en ny triangel, eftersom vinklarna på 90° passar ihop och bildar en linje. Men notera att den stora triangeln har alla vinklarna lika med 60°, därför är den liksidig. Alltså är c = 2a.
Nu är det lätt att räkna ut sinus av vinkeln 30°.
På så sätt är det rätt enkelt att lista ut vad cos 60° är för någonting. Det är nämligen samma som sinus 30°, eftersom om vi kollar på de två olika spetsiga vinklarna i en rätvinklig triangel, så blir enas motstående sida den andras närliggande och tvärtom. Hypotenusen är densamma.
Men hur tar vi reda på sin 60° (och samtidigt cos 30°)? För det måste vi bestämma förhållandet b/c. Men eftersom 
(Pythagoras sats), så kan vi i vårt fall skriva:
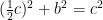
så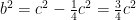 
Eftersom alla längder är positiva har vi 
och då är
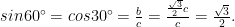
Och hur gör vi nu med vinklarna 0°, 45°, 90° grader? Det går faktiskt att rita upp motsvarande triangel och ”triangel”. Fundera på vad sinus och cosinus för de respektive viklarna blir. Faciten kommer i nästa del.
Om man minns de här trianglarna är det möjligt att alltid räkna ut sinus eller cosinus som man behöver. Men om det är lite svårt med geometrin, finns det en rätt bra minnestabell.
Skriv upp alla ”kända” vinklar: 0°, 30°, 45°, 60° och 90°. Deras sinus och cosinus följer då ett intressant mönster:
