Du kan läsa om vad som har hänt på de tidigare träffarna här: första träffen, andra träffen och tredje träffen.
Introduktion till informationsteori
Vi började lektionen med leken ”Gissa talet”. Jag tänkte på ett tal mellan 1 och 10 och eleverna fick ställa ”Ja/Nej”-frågor för att försöka bestämma vilket tal jag tänkte på. Jag tror att det tog 5 frågor för dem att bestämma talet.
Här ska man vara tydlig om vad som gäller sista frågan. Ska man veta vilket tal det är efter x frågor eller ska man med fråga nummer x bekräfta talet? I uppgifterna räcker det att man vet vilket tal det ska vara, men man behöver inte fråga specifikt om det. Till exempel, om man vet att talet är 3 eller 4, frågar ”Är talet 3?” och får svaret ”Nej”, så behöver man inte fråga något mer, utan talet räknas som gissat.
Jag undrade sedan om hur många frågor som krävdes som mest för att garanterat gissa ett tal mellan 1 och 10 på det här sättet. Eleverna tänkte att 5 frågor räckte, men var osäkra på om 4 frågor var nog.
Startuppgiften var till för att presentera idén informationsteori, det vill säga hur mycket information man egentligen får när man det bara finns ”Ja” och ”Nej” som svar på frågorna. Hur mycket information är nog för att gissa talet?
Informationsteori: problemlösning och genomgång
Vi delade ut dagens uppgifter sedan och eleverna löste dem, mestadels på egen hand. För att alla ändå skulle ta del av varandras idéer körde vi genomgångar på tavlan allt eftersom. Då kunde eleverna snappa upp lösningssätt direkt för att eventuellt tillämpa dem på senare problem.
Problemen försökte jag ordna i svårighetsgrad, så att man successivt skulle sättas in ämnet och idéerna. Efter varje problem skriver jag dialoger jag hade med enskilda elever, samt med gruppen när vi gick igenom respektive uppgift på tavlan.
1. Du och en kompis spelar ett spel där ni ska ge varandra hemliga signaler. Ni har kommit överens om att man antingen kan blunda med ena ögat, med båda ögonen eller ha ögonen öppna, samt röra på vänster lillfinger eller hålla vänstra lillfingret still (alla andra rörelser spelar ingen roll, och görs för att avleda motståndarna från systemet). Hur många olika kombinationer av signaler kan du göra?
Elev: Jag vet inte om det räknas som samma eller olika om man blundar med höger- eller vänsterögat.
Lärare: Vi räknar det som olika i den här uppgiften.
Elever: Då har jag ritat upp alla möjligheter och det blir 4*2 = 8.
Lärare: Rätt!
2. Vilgot tänker på ett heltal mellan 1 och 8. Theo ställer frågor, som Vilgot bara kan svara ”ja” eller ”nej” på. Theo vill bestämma talet.
a) Kan han bestämma talet på tre frågor?
b) På två frågor?
Elev: Så här kan man göra med tre frågor (visar frågorna som man kan ställa och hur man fortsätter beroende på svar).
Lärare: Javisst, tror du det går med två frågor?
Elev: Nej, inte alltid.
Lärare: Varför inte?
Elev: Vet inte riktigt..
Gruppdisskussion:
Lärare: Ni har kommit på olika sätt att ställa frågor så att man kan gissa talet garanterat på tre försök. Går det att hitta på frågor som alltid är desamma oavsett vad personen svarar?
Elever: De första två går. Först frågar man om talet är större än 4 och sedan huruvida det är udda eller jämnt.
Lärare: Japp, det funkar att ställa den andra frågan oavsett svaret på den första. Men går det med alla tre? Tänk på det…
En annan lärare: Jag vet hur man gör, men det är ganska komplicerade frågor…
Lärare: Det går inte med två frågor, varför inte?
Elev: (Berättar om halvering)
Lärare: Precis, det är en möjlig förklaring, här är en annan! (Berättar om hur man beräknar information för att särskilja mellan möjliga kandidater.)
3. På en balansvåg kan man jämföra vikten i vänsterskålen med vikten i högerskålen. Vågen kan antingen visa balans eller att vänsterskålen är tyngre eller att högerskålen är tyngre. Emilia experimenterar med att väga olika mynt för att jämföra dem med varandra. Klara antecknar resultatet av varje vägning på ett papper.
Emilia gör 5 vägningar. På hur många sätt kan Klaras protokoll se ut?
Elev: Första vägningen kunde se ut på tre sätt. Sedan är det liksom en förgrening, där det kan se ut på tre sätt till efteråt. Jag försöker skriva upp alla kombinationer.
Lärare: På hur många sätt kunde då protokollet se ut efter 2 vägningar?
Elev: 3*3 = 9
Lärare: Och efter tre? Och efter fem?
Elev: Ahaa.. 35.
4. 9 mynt ser likadana ut. Man vet att exakt ett av dem är falskt (men man vet inte vilket). Man vet även att alla äkta mynt väger lika mycket samt att det falska myntet är något lättare. Hur kan man bestämma det falska myntet med högst två vägningar? Går det att göra det på en vägning?
Elev: (Visar hur man gör med två vägningar).
Lärare: Rätt. Varför går det inte att göra på en vägning?
Elev: Hur man än gör så blir det en hög över som man inte vet något om.
Lärare: Men kan man inte lämna 1 mynt över och väga de andra?
Elev: Jo, men då vet man fortfarande inte vilket som är falskt, om det inte blir lika.
Det var inte så många som kopplade ihop uppgift nummer 3 och nummer 4. Jag förklarade sedan högt att man kan göra precis som i uppgift 2, fast istället för ”halvering” har vi ”tredelning”. Eller, om man gör på det andra sättet, så ska vi ha resultat som skiljer på 9 mynt, men vi kan bara få 3 olika resultat (”protokoll”).
5. Det finns 6 mynt, varav 2 är falska och väger mindre än de riktiga. Hur många vägningar behöver du som minst för att säkerligen bestämma de båda falska mynten?
En av eleverna visade korrekt resonemang för tre vägningar, men det var en annan lärare som kontrollerade detta. Tillsammans gick vi igenom den lösningen på tavlan. Sedan gällde det att motivera varför detta inte gick att göra på två vägningar.
Lärare: Nu är det inte ett mynt man ska bestämma, utan två. Hur många ”situationer” behöver vi skilja emellan? På hur många sätt kan 2 mynt av 6 vara falska?
Elever: (Kommer fram till att det är 15).
Lärare: Så vi har 15 misstänkta situationer. På hur många sätt kan protokollet se ut efter 2 vägningar?
Elever: 9.
Lärare: Alltså går det inte att skilja mellan 15 olika situationer, så det går inte att säkerligen bestämma de falska mynten på 2 vägningar.
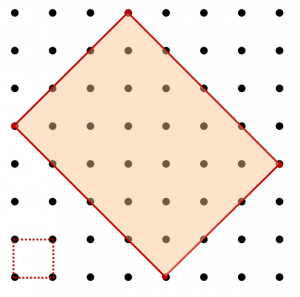
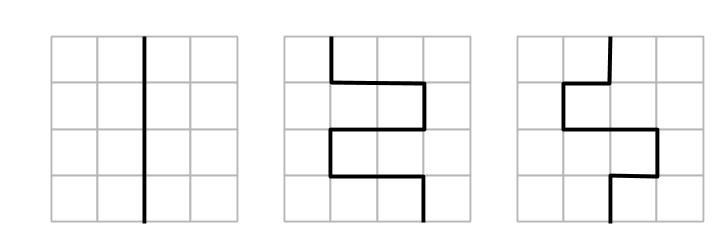
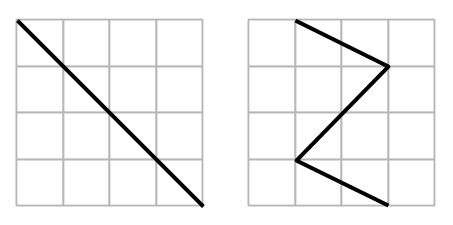
6. En liksidig triangel är uppdelad i 9 små kongruenta liksidiga trianglar. Benni markerade en av de små trianglarna med osynligt bläck. Ivar kan peka på en triangel, vars sidor går längs med de utritade linjerna och då måste Benni svara huruvida den markerade triangeln ligger i den Ivar pekar ut.
Hur många frågor behöver Ivar som minst för att garanterat hitta den markerade triangeln?
Denna uppgift hanns inte med, utan den blev kvar i läxa. Jag förtydligade vilka regler som gällde på tavlan, nämligen visade upp exempel på trianglar med olika storlekar som man kunde peka ut vid frågor.
Skottväxling
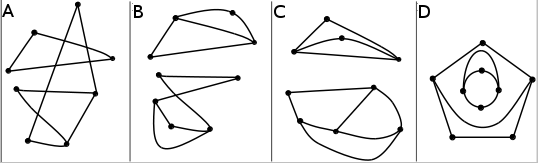
Andra (lite mindre) halvan av lektionen körde vi mattetävlingen ”Skottväxling”. Eleverna delades upp i lag om tre personer. Lagen fick de kreativa namnen A, B, C och D.
Reglerna till Matematisk Skottväxling är följande:
Varje uppgift ger ditt lag rätt till ett skott. Ange ert svar på en papperslapp och skriv vilket lag ni skjuter på. Var femte minut verkställs anmälningar i samma ordning som de har kommit. Fel svar räknas som ett ett klickskott och minskar er träffsäkerhet. Vid rätt svar slumpas det (beroende på er träffsäkerhet) huruvida ni träffar eller missar.}
Träffar ni så minskas den träffade lagets styrka med 1/5 av er styrka (en kvot avrundas neråt).
Är er styrka mindre än 15, så minskar er motståndares styrka med 3.
Efter spelets slut vinner den som är starkast då. Ursprungliga styrkor är 100.
Den ursprungliga träffsäkerheten är 2:2, det vill säga 2 chanser att träffa och 2 att missa.
Rätt svar ökar era chanser att träffa med 1, fel svar ökar era chanser att missa med 1.
Uppgifterna är indelade i 2 delar, del 1 ges ut i början, del 2 ges ut 20 minuter efter start. Spelet är slut antingen när det har gått 40 minuter eller när alla har skjutit sina 10 skott.
Ett lag får lämna svar på varje uppgift i godtycklig ordning och vid valfri tidpunkt, men inte mer än en gång per uppgift.
(Detta stod inte i reglerna, men vi förtydligade vid start att chanserna förändrades innan skotten avfyrades).
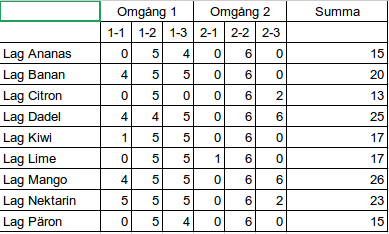
Vi körde tävlingen i två delar med 5 problem i varje. De flesta inlämnade svar var korrekta, så många skott under tävlingen träffade. Vi skrev upp protokoll direkt under tävlingens gång över vem som sköt på vem och hur mycket lagen minskade i styrka. Det var roligt att följa hur vissa lag ”förklarade krig” mot varandra då och då. Det var ganska mycket action och vi fyra lärare var sysselsatta nästan hela tiden!
Detta är ju en lek som det är svårt att ha vinnande strategi i, eftersom man alltid kan skjuta på den som leder. Men man kan vara lite taktisk med tidpunkter då man lämnar in sina svar.
I slutändan stod lag D som segrare efter en ganska jämn match! Tyvärr har jag inte sparat poängtabellen.
Här kan du själv prova att lösa Skottväxling-uppgifterna. Fråga mig om du vill veta de rätta svaren. Notera att den sista uppgiften på del B är lite annorlunda från de andra. Den är baserad på en uppgift som en av eleverna på Matteklubben kom på. Den var dock ändrad för att eleven inte skulle ha för mycket fördel i tävlingen.
På del A var uppgift 2 och 3 lättast och på uppgift 5 gavs flest felaktiga svar. Vi gick igenom den uppgiften i slutet av lektionen.
På del B gavs flest rätt svar på uppgift 3 och 4, medan 2 och 1 svarade de flesta fel på. Ingen löste uppgift nummer 5 (den var nog överkurs).
Prova gärna att organisera skottväxling i den egen klass! Det är roligt för de flesta, eftersom vilket lag som helst, oavsett styrka, har möjlighet att vinna. Anpassa uppgifterna efter elevernas nivå.
Hos oss var tävlingen i alla fall populär, vilket märktes på utvärderingarna. De flesta av eleverna i den här gruppen känner inte varandra så det var bra att ”tvinga” dem att samarbeta lite.
Utvärdering
I slutet av lektionen fick eleverna svara på följande frågor om matteklubben:
Vilken matteklubben-träff tyckte du bäst om?
Vilket tema var mest intressant?
Vilket avsnitt var svårast?
Vad kan fungera bättre med matteklubben?
Vill du se någon förändring inför nästa termin? Vad i så fall?
Vill du fortsätta gå på Matteklubben nästa termin (ringa in)?
Ja Nej Kanske
Det är lite konstigt ser jag nu att vi inte bad eleverna att bedöma deras insats, så som vi gjorde i de yngre årskursna. Vi missade nog helt enkelt att inkludera den frågan.
Resultatet av utvärderingarna
Efter varje svar står siffran för antalet elever som gav det svaret.
Vilken matteklubben-träff tyckte du bäst om?
– Den sista 7 (2 säger: för att det var tävling)
– Vet inte 2
– Nr 3
– Ingen var utmärkande
– Informationsteori
Vilket tema var mest intressant?
– Alla var ungefär lika intressanta 2
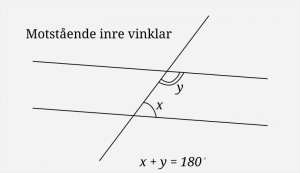
– Vinklar
– Informationsteori 5
– Delbarhetsprinciper
– Vet inte/ej svar 3
Vilket avsnitt var svårast?
– Vinklar 4
– Vet inte/ej svar 5
– Alla var bra anpassade så ingen var speciellt svår
– Andra lektionen 3
Vad kan fungera bättre med matteklubben?
– Ingen aning/Vet ej/ej svar 9
– Lättare uppgifter
– Mer tävlingar
– Tydligare vilken sal man är i
– Lite tidigare möten
Vill du se någon förändring inför nästa termin? Vad i så fall?
– Att varje person ska få göra en uppgift och så kan vi lösa varandras
– Vet ej/ej svar 7
– Lite tidigare möten
– Mer tävlingar
– Lättare uppgifter
– Jag vill ha det tidigare i veckan
– Enda förändringen jag vill se är hos mig själv och mina kunskaper. Matteklubben är bra!
Vill du fortsätta gå på Matteklubben nästa termin (ringa in)?
Ja 6
Nej 0
Kanske 6
Tankar inför nästa termin
Jag tänker precis som eleverna: mer tävlingar, bättre anpassad svårighetsgrad! Jag ska försöka köra tävlingar var tredje gång även i den här gruppen eller kanske en större tävling var fjärde gång och en minitävling var fjärde gång. Vi behöver även att träna på fler redovisningsformer, t.ex. ha skriftliga lösningar någon gång. Tyvärr kan inte vi ha Matteklubben tidigare på dagen, på grund av svårigheten att boka salarna tidigare.
Med en så pass liten grupp borde jag ha hunnit lära mig allas nivå och styrkor, men det har visat sig vara rätt svårt. Eleverna har varit ganska tysta under lektionerna och jag har själv uppmanat dem till att redovisa lösningar, åtminstone till mig. Vi får se om det blir bättre med tiden, att eleverna känner sig säkra på sin problemlösningsförmågor samt att det är helt ok att ha fel på Matteklubben. Nästa termin kan bara bli bättre! :)