Ihoplimmad kub
Av 27 kuber av storleken 1x1x1 limmade man ihop en kub av storleken 3x3x3 genom att alla kontaktytor limmades. För att limma ihop två sidor använde en droppe lim varje gång. Hur många droppar lim använde man totalt?
Andra träffen med Matteklubben, åk 2-4
Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.
På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i årskurser upp till 4 är mycket aktiva och berättar gärna sina lösningar. Vi var 6 lärare och 29 elever. Ju yngre barnen är, desto lägre måste elev/lärare-kvoten vara, enligt min erfarenhet ungefär 4-5 för yngre barn och 6 (absolut högst 7) för äldre barn.
Blandade problem
Lektionen började med att eleverna satt två och två och löste blandade problem, precis som vi brukar göra med de äldre grupperna. Under varje uppgift står vanliga dialoger som jag och de andra lärarna hade med eleverna.
1. Andreas skrev upp talen i ordning tills siffran 2 skrevs upp 10 gånger. Han började med talet 1. Vilket tal slutade Andreas på?
Elev: 92, för att han började på 2, sedan är det 12, sedan 22, 32, 42, 52, 62, 72, 82, 92. Tio tal ger tio tvåor!
alternativt:
Elev: 82, för att han började på 2, sedan är det 12, sedan 22 (två tvåor), 32, 42, 52, 62, 72, 82. Tio tvåor!
Lärare: Måste tvåorna som skrivits upp alltid vara den sista siffran? (Pekar på 22.) Här är det en tvåa som talet börjar med. Finns det inte fler sådana tal?
Elev (efter en liten tankestund): Ja, just det, det är så på 20, 21, 22… Räknar snabbt fram till talet 26 (eller 27 om den andra tvåan i 22 glöms bort).
2. Så fort deltagarna ankom till Matteklubben bildades det en lång kö till fikat. Precis bakom Adam står Linda, precis bakom Linda står Hjalmar. Om man räknar från köns början, står Hjalmar som nummer tjugo. Om man räknar från slutet, står Adam som nummer trettio. Hur många personer står i kön till fikat?
Elever: Är svaret 46?
Lärare: Kanske, berätta hur ni tänkte!
Elever: Om Adam är nummer 30 från slutet, så är det 27 personer bakom Hjalmar i kön. På samma sätt är det 17 framför Adam. Mellan Adam och Hjalmar är det 2 (personer). Tillsammans blir det 27 + 17 + 2 = 46.
(Det fanns också andra förklaringar till 46 som jag måste erkänna att jag inte riktigt förstod. Det var inte helt lätt att fånga upp felet i resonemang där man är slarvig med att räkna med/inte räkna med personer som står på ändarna)
Lärare: Vilka personer har vi räknat in och vilka har vi inte räknat in? Har vi räknat någon två gånger?
alternativt:
Lärare: Om det är 27 personer bakom Hjalmar, hur många är resten? Alltså från nummer 1 till Hjalmar som är nummer 20? (Det var inte helt självklarat för vissa barn att det var 20.)
3. Med hjälp av siffrorna 0, 5 och 9 bilda det största möjliga samt det minsta möjliga tresiffriga talet. Siffrorna i talet måste alla vara olika.
Elev: Det är 905 och 059.
Lärare: Men 059 räknas inte som tresiffrigt.
Elev: Aha, då är det 509.
4. Tre ekorrar hittade 90 nötter. De delade upp nötterna på så sätt att den äldsta ekorren fick 10 nötter mer än mellanekorren och så att den yngsta ekorren fick 10 nötter mindre än mellanekorren. Hur många nötter fick varje ekorre?

Elever: Vi tänkte först att alla skulle få lika många nötter, 30 stycken. Men sedan skulle den minsta ge 10 till den största, så det blev 40, 30, 20.
alternativt:
Elever: Vi testade med 30, 20, 10, men då blev det för lite. Det saknas 30 nötter. Då lade vi på 10 till varje ekorre.
5. På en idrottslektion ställde sig hela klassen på en rad. Först skulle var sjunde barn göra två steg fram. Sedan skulle var tredje barn (av de som var kvar i ledet) göra ett steg fram, och till sist skulle var femte barn (av de som var kvar) göra ett steg bakåt. Hur många går i klassen om 15 barn stod kvar på sina platser i slutändan?
Elever: Är svaret 30?
Lärare: Låt oss kontrollera!
(Vi kontrollerar för 30 genom att rita upp 30 pinnar/saker, stryker dem en i taget och ser att det fungerar.
Lärare: Finns det fler svar?
Några av elevparen blev klara med uppgifterna snabbt, och då fick de lösa ett par extra uppgifter från träffen med åk 5-6.
Sedan var det dags att presentera lösningarna på tavlan. Många av eleverna/grupperna var ivriga att få gå fram. För att fler skulle få komma fram fick de göra det två och två. De som var bekväma med att prata inför gruppen fick presentera lösningen, de andra agera som stöd (ibland turades båda om att prata).
Eleverna hade snygga (förfinade efter diskussion med läraren) lösningar på uppgifterna. Till exempel, på uppgift 1 skrev de bara upp talen från 1 till 26 som innehöll siffran 2 (eftersom de andra var irrelevanta). På uppgift 2 ritade eleverna upp hur de tänkte, vilket nästan påminde om Venn-diagram, man kunde lätt följa deras resonemang. Efter att uppgift 3 hade presenterats frågade jag hur man i allmänhet bildade största möjliga och minsta möjliga tal med en given mängd siffror. Barnen kunde svara på det utan problem, även om vissa först tänkte att 0 kunde stå på första plats i ett tal (även någon enstaka lärare trodde att det var ok).
Fixering vid svar
Det jag har märkt både under diskussionerna med eleverna och i sättet de presenterar lösningarna på tavlan är att de lägger stor vikt vid att formulera svaret. De tycker att det absolut ska stå ”Svar:” någonstans på pappret (eller när man presenterar på tavlan). Eller så glömmer de ibland bort att skriva det, men när de är färdiga med lösningen kommer de ihåg att avsluta med ”Svar: 30 elever” till exempel.
Detta läggs förstås vikt på i skolan, för att läraren lätt ska få en överblick över om uppgiften gjorts rätt eller inte. Under Matteklubben försöker jag skifta fokus från svar till själva lösningar. På frågan ”Är __ rätt svar” svarar jag alltid ”Hur tänkte ni?” för att visa att det är tanken och inte vad man räknade ihop på slutet, som räknas. Extra roligt är det att ta med uppgifter där det finns flera svar på lektionerna. Då förstår eleverna bättre när läraren ställer frågorna ”Finns det fler svar på uppgiften? Varför/varför inte?”. De börjar undersöka mer för att själva försäkra sig om att de verkligen har betraktat alla möjligheter. Vi straffar inte elev för att hen har gissat sig fram till ett svar, för det är också en slags strategi (som kan ge rätt svar), men vi försöker säga att det inte räknas som en fullständig lösning förrän man är säker på att det inte finns fler svar.
Det var det som hände vid diskussionen av uppgift 5, då vi kom fram till att det finns ett ytterligare svar än det som presenterades på tavlan. Men därefter kunde vi också förklara varför antalet elever i raden inte kunde bli större eller mindre.
Experiment med utvikningar
Nu fick eleverna vara i gruppen om 3-5 och undersöka olika utvikningar. Varje grupp fick en sax och en linjal, samt papper för att klippa ut och testa utvikningar. Till uppgift 2 tog jag med en Rubiks kub som fick stå framme på katedern. Om man ville testa sin utvikning, fick man alltså komma fram och göra det. Till uppgift 3 tog jag med några tändsticksaskar (därav måtten) som eleverna också kunde testa utvikningar på. Men det var nästan ingen som hade kommit så långt.
Eleverna var lite mer trötta vid det här laget och hade svårigheter med att läsa igenom och skilja på de olika uppgifterna. Jag sade till många att de skulle komma på egna utvikningar, men då läste ju inte eleverna uppgift 2 så noga (eftersom de antog att de redan hade fått det förklarat) och många missade att sidan skulle vara 6 cm. Inte för att det gör särskilt mycket. Men nästa gång ska jag ha tydligare gräns mellan uppgifterna, kanske till och med ge ut dem en i taget.
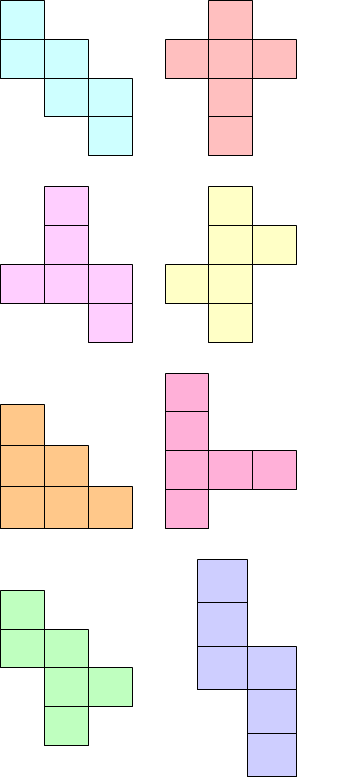
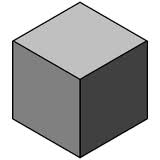
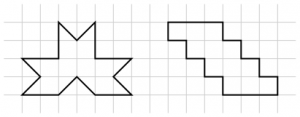
1. Vilka av figurerna på bilden kan vecklas ihop till en kub?
Vissa elever föreställde sig hur det skulle bli i huvudet (och då gjordes såklart också några fel) och kunde utesluta eller godkänna några former. De flesta klippte ut och testade med papper när de var osäkra. Den metoden fungerade perfekt. Några av eleverna sade att de redan hade gjort liknande uppgifter tidigare på lågstadiet och då kan man ju bara glädjas åt att de verkar ha haft roligt då i skolan. Jag hoppas dock att alltid lära ut något extra med uppgifterna på Matteklubben, så som diskussionen nedan.
2. Hitta på en annan utvikning till en kub och tillverka den. Kubens sidor är 6 cm långa. Klipp ut din utvikning och testa den på kuben.
Några grupper gjorde en egen utvikning i rätt storlek, några gjorde mindre utvikningar. Det bästa med stora utvikningar var att vi kunde testa dem på Rubiks kub och alla kunde se att det passade. Många grupper hittade den utvikningen, som är lik den första, fast man flyttar två av rutorna (så att formen ser ut som bokstaven ”T”). Då uppmanade jag dem att hitta på en till.
3. Kom på en utvikning till ett rätblock som är 1,5 cm hög, 4 cm bred och 5,5 cm lång. Klipp ut och testa utvikningen!
Under tiden någon klipper ut utvikningen, försök att komma på fler annorlunda utvikningar till samma rätblock. Du behöver inte rita dem snyggt, bara på ett ungefär.
En grupp tillverkade utvikningen och vi testade den sedan på tändsticksasken. Möjligen hade de flesta grupper inte hunnit komma så långt, då vi inte hade så mycket tid för det här momentet.
Diskussion
Vi ritade upp alla utvikningar (inklusive de falska) från uppgift 1 på tavlan och gick igenom dem en och en och klassen fick skandera ”ja” eller ”nej” som svar på frågan huruvida de var möjliga eller inte. De flesta hade alla rätt. Vi markerade även vilka rutor som var tvungna att överlappa ifall man skulle klippa ut figuren och försöka vika en kub utav den.
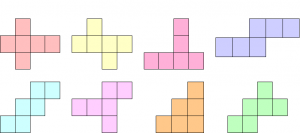
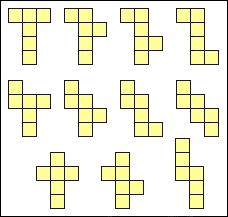
Sedan var det dags för grupperna att lämna in utvikningar som de själva hade kommit på. Det blev tre annorlunda former totalt och de ritade vi upp (och visade upp de stora). Jag berättade att det totalt finns 11 utvikningar så om man ville, kunde man försöka hitta de 2 vi saknade. Här bifogar jag en bild över alla ifall man är nyfiken:
Sedan visade vi upp utvikningen för ett rätblock som en grupp hade gjort (som var korrekt och inspirerad av standardformen (”plus”) på kubutvikningen). Då ställde vi en fråga till barnen: ”Tror ni att finns fler utvikningar för en rätblock än för en kub eller färre?”. ”Färre!” skanderade barnen. De tänkte att det var svårare att rita upp en utvikning för ett rätblock (svårare att passa in sidor), alltså måste det finnas färre sådana.
Då försökte vi diskutera fram till att om en utvikning för ett rätblock kan göras av en kub-form, skulle en inte då kunna göras av andra kubformer också? Långsamt blev barnen mer och mer övertygade om detta. ”Lika många, lika många!” skrek de då.
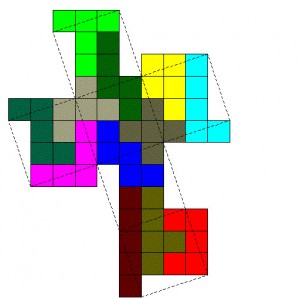
Sedan ritade jag och en annan lärare upp flera olika former för rätblock som egentligen hade samma underliggande standardutvikningsform för kuben. Vi kunde variera den på minst tre olika sätt, genom att välja form och riktning på ”sidoflärparna” (det finns ju tre olika rektangelytor). Då började fler och fler barn långsamt bli övertygade om att de faktiskt fanns fler former för rätblock (som inte är kuber) än för kuber. Jag avslöjade att det fanns ungefär 50 utvikningar för rätblock. ”Och vi ska hitta de alla!” sade en elev med uppspärrade ögon. Kul tänkt, men matte ska ju helst inte var plågsamt :) Så det behövde de förstår inte göra, men jag bifogar de ändå här:

Hemuppgift
Det fanns extrauppgifter på bladet som de flesta inte hann komma till. Därför fick de ta dem med sig hem och tänka över dem i lugn och ro. Hemuppgiften är förstås frivillig.
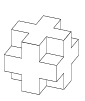
Konstig nog går även den här formen att vika ihop till kub (testa hemma)!
Kan följande former också vikas ihop till kuber?
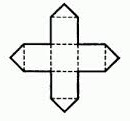
Jag berättade om vad den första uppgiften gick ut på (att man skulle klippa ut den delen som var i färg). Barnen blev väldigt förvånade över att det var en utvikning (”hur ska man vika ihop den då?”). Då tipsade jag om att det fanns en ritning över kuben, som var sned och att man kunde ta den som grund. Då förstod en av eleverna att de bitarna som stack ut passade ihop precis med det som saknades på rutorna bredvid. Får se om någon tar sig an de sista tre formerna och lyckas vika ihop dem till en kub. Det är inte särskilt lätt ens för vuxna!
Utvärdering
De 29 eleverna som kom till lektion kände sig motiverade och trivdes bra (förutom för en elev som var där för första gången och inte hade roligt), så gruppen är rolig att arbeta med. Nivån var till och med enkel för många, så det gäller att ha ett förråd med svårare uppgifter, ifall någon blir klar väldigt fort (t.ex. uppgifter från åk 5-6 kan passa). Barnen blev fortfarande trötta mot slutet, men eftersom uppgifterna var mer tillgängliga än första gången, orkade nästan alla jobba hela vägen fram.
En annan lärare påpekade, efter att han på en rast hjälpt en elev att fatta lösningen på uppgiften om fikakön, att det viktigaste med matten är inte att fatta, utan att försöka fatta. Kloka ord tycker jag, Har man nyfikenheten och ihärdigheten, så kan man komma hur långt som helst!
Måla kubens yta
Måla kubens yta
[kkratings]
För att måla ytan på en kub av storleken 2x2x2 krävs det 2 gram färg. Hur mycket färg krävs det för att måla ytan på en kub av storleken 6x6x6?
Datum med träblock
Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.

Tre av dem är av avlånga och används för månaderna.

De andra två är kuber. Vilka siffror kan stå på kubernas sidor för att man ska kunna bilda alla datum?
Rubiks kub utan hörn
Rubiks kub utan hörn
[kkratings]
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1×3-kuber?
En lektion för små barn i mönster och spatial förmåga
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Här kan du se vad vi tidigare har gått igenom.
Mönster
Väldigt mycket i matematiken handlar om att se mönster. Jag skulle vilja påstå att det mesta inom grundskolans matematik går ut på att lära sig se ett slags mönster i uppgifter för att kunna tillämpa metoder.
Mönster som 3 + 7 = 10 hjälper en att lösa uppgifter som 14 + 3 + 7 = 24.
Och ifall man är bra på att extrapolera mönster, kan man komma på formler alldeles själv!
Upprepningar
Gjorde ni också girlanger utav gubbar till julgranen? Pojkarna nedan är ganska enkla att göra, men hur gör man för att klippa ut en girlang med varannan kille, varannan tjej?

Se mönstret och fortsätt
Ett bevis på att man ser mönstret i bilden är att man kan fortsätta det. Och tvärtom, om man försöker fortsätta mönstret ser man kanske när det blir fel och när det blir rätt.
Om man väver några remsor kan man se ett mönster i hur de synliga bitarna är färgade. Vilka färger finns underst respektive överst där bokstäver A och E står?

Föreställ dig mönstret
Ju mer matematik man läser, desto mer behöver man tänka abstrakt. Det innebär ofta att föreställa sig saker som inte finns framför en. Ibland föreställer matematiker sig saker som ingen har sett (som till exempel fyrdimensionella objekt)!
Förmågan att föreställa sig fysiska objekt och förhållandet dem emellan kallas för spatialförmåga. Den är väldigt viktig för pilot- och militäryrket, och så förstås matematikerna. För att träna den skall de lite äldre barnen lösa följande pussel:

Utan att kvadratbitar får klippas ut och arrangeras om, skall man bestämma vilken på som ska vara på vilken plats. Det betyder att bitarna måste arrangeras om i huvudet. Du kan prova själv genom att fylla i en en följande tabell med motsvarande tal.

Föreställ dig något som inte syns
En klassisk uppgift är att bestämma hur många kuber ingår i konstruktionerna, utan att alla kuberna syns.
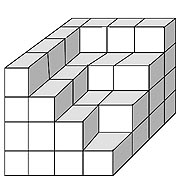
Efter att alla barnen har skrivit ner förlaget, bygger vi upp sktrukturen och räknar hur många kuber det faktiskt behövdes.
Perspektiv
De äldre barnen får träna spatialförmågan på ett tredimensionellt sätt. De får se en bild på kubens alla sidor (i utvikt format), och sedan avgöra hur tre av kubens sidor ska se ut när man kollar på den från olika vinklar.
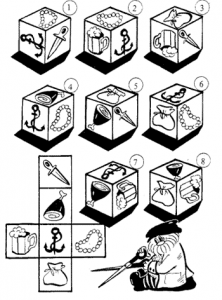
Tillverka en kub
Vi ska kombinera några av de ovastående övningarna och tillverka en kub själva. För det första skall barnen lista ut vilka av kvadraternas sidor skall tejpas ihop med vilka. Sedan får alla ett papper med ett mönster.
Uppgiften är nu att klippa upp mönstret i 6 likadana kvadrater. Varje kvadrat klistras sedan på en av sidorna på någons kub.
Det svåra är att klippa exakt utan att mäta. Tricket är att kolla på kanten, till exempel den vänstra. Då ska man klippa i bilden precis där den vänstra kanten av högra halvan är likadan som vänstra kanten av vänstra halvan. Skriv ut och försök själv!

En heltalskub
En heltalskub
[kkratings]
För en viss kub räknade man ut följande tre tal: summan av alla sidlängder, ytan, samt volymen. Alla talen, uttryckta i centimeter/kvadratcentimeter/kubikcentimeter, är tresiffriga heltal. Hur lång är kubens sida?
Problem vecka 8. Tävlingsstart!
Kuben (1 poäng). En träkub har sidlängden 1 m. Vi sågar upp kuben i små kuber som alla har sidlängden 1 cm och lägger alla småkuberna på en rad. Hur lång blir raden?
Siffertriangeln (3 poäng). Går det att fylla de gula cirklarna med siffrorna från 0 till 9, så att summan längs med valfri av de 6 sträckorna blir densamma?

Visa lösningar
Adventspyssel 14
Finns det något bra ord för att någonting är någon yta, fast utvecklad och tillplattad? Det heter i alla fall ”net” på engelska.
Möjliga kuber
Lösning till problem vecka 23
En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta sidan vrida sig 90 grader i förhållande till startläget?
Svar:
Nej, det kunde den inte.
Lösning:
Låt oss beteckna kubens hörn med (sidan
ligger precis under sidan
). Föreställ er att finns en liten tetraeder
som är gjord av ett annat material. Vi kommer att följa den tetraederns position allt eftersom tärningen rör sig.
Om tärningen rullas över en gång, kommer tetraedern befinna sig i samma läge som hade från början, fast parallellfärflyttad. Och vice versa,
avbildas på en parallellförflyttning av tetraedern
.
För att tärningen ska komma tillbaka tillsamma ruta, måste den rullas ett jämnt antal gånger (föreställ er ett schackbräde på bordet, då byter rutan färg efter varje steg). Det innebär att den annorlunda tetraedern kommer att avbildas på sig själv.
Men om den översta sidan vrids 90 grader, så avbildas sidan på sidan
, men den sistnämnda ligger utanför tetraedern av annorlunda material. Motsägelse.
© 2009-2025 Mattebloggen