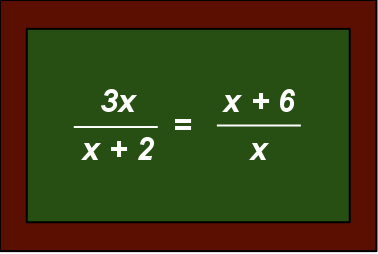I veckan besökte jag Matematikbiennalen i Karlstad, en stor händelse för mattelärare, där ett par tusen besökare fick vara med om föreläsningar, workshops och utställningar. Allt handlade om matematikundervisning.
Jag höll i en föreläsning där jag delade med mig om mina erfarenhet kring problemlösningslektioner. Följande poänger försökte jag få fram:
– Lektioner i matte följer nödvändigtvis en struktur pga förutsättningar och omständigheter, men man kan variera undervisningen genom att erbjuda eleverna helt olika sorters problem.
– Poängen med problemlösning är att man ställs inför problem man aldrig tidigare mött förut och vänjer sig vid att vara bekväm med det.
– Man kan ha ett problem som inslag i en lektion (där passar kluringar) eller ha en problemserie, där det också finns olika sätt att lägga upp det på.
– Det finns allmängiltiga ledtrådar man kan ge, men ledtrådarna kan även vara anpassade till varje elev om man ser vart hen är på väg.
– Elever som är svaga i problemlösning tjänar på att bli inkluderade via lek eller se att alla kan ha fel, även de bästa eleverna och läraren.
– Matematikens historia ska tas upp för att ge perspektiv på att eleven redan har lärt sig minst 1000 års visdom.
– I mattetävlingar som sker på lektionstid ska man kunna lämna in svar flera gånger för att bli uppmuntrad att försöka på nytt.
– Ge helst problem där man vill ta reda på svaret, eftersom att man KAN ta reda på svaret är inte uppbart från formuleringen.
– Problemlösnings finns till för att fostra matematiska färdigheter (sanningssökande, kreativitet, etc.) men också för att stärka matematiskt självförtroende, upptäckarglädje och njutning av vackra lösningar.
För konkreta exempel på problem och lektioner kan du ladda ner och bläddra igenom föreläsningen: